演算法設計與分析(十一)--動態規劃
阿新 • • 發佈:2018-12-21
1. Unique Binary Search Trees
2. Unique Binary Search Trees II
Unique Binary Search Trees
題目
Given n, how many structurally unique BST’s (binary search trees) that store values 1 … n?

分析
這題是典型的卡特蘭數的例子,首先我們先來了解一下卡特蘭數是什麼,
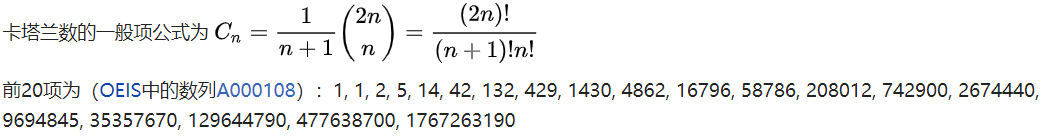
其遞推公式為
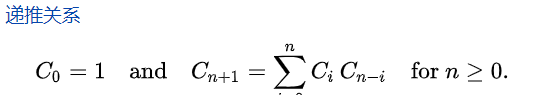
這道題就是根據這個遞推公式進行求解。
對於這題,遞推公式的具體含義是:
dp[0] = 1
dp[1] = 1代表是1作為根,則明顯有一種情況。
dp[2] = dp[0] * dp[1] + dp[1]*dp[0], 代表有兩個數,當1為根時,有dp[0]*dp[1]種情況;當2為根的時候,有dp[1]*dp[0]種情況。
dp[n] = dp[0]*dp[n-1] + dp[1][n-2] + … +dp[n-1]*dp[0]
根據上述的推導過程,我們可以容易得出狀態轉移方程:
dp[i] += dp[j]*dp[i - j - 1];
原始碼
class Solution { public: int numTrees(int n) { vector<int> dp(n+1, 0); dp[0] = 1; dp[1] = 1; for(int i = 2; i <= n; i++) { for(int j = 0; j < i; j++) { dp[i] += dp[j]*dp[i - j - 1]; } } return dp[n]; } };
Unique Binary Search Trees II
題目
Given an integer n, generate all structurally unique BST’s (binary search trees) that store values 1 … n.

分析
這題是第一題的加強版,這次不是求二分搜尋樹的不同種類,而是將具體每一種情況都求出來,這意味著我們需要記錄好每種二分查詢樹的狀態。
由於這些狀態是相對連續的過程,所以這題我們可以與矩陣乘法的動態規劃實現做類比。
我們用dp[i][j]表示從i開始到j這個子問題的解的狀態,而對應的這個狀態我們可以在dp[i][j]中多加一維來記錄。
同樣的道理,我們將dp[i][j]這個狀態分成dp[i][k-1]和dp[k+1][j]兩格狀態來解決。
除了這些以外,我們還需要注意樹的構建,在分解為子問題的時候,注意要維持樹的狀態。
原始碼
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<TreeNode*> generateTrees(int n) {
vector<TreeNode*> **dp = new vector<TreeNode*>*[n+1];
for(int i = 0; i < n+1; i++) {
dp[i] = new vector<TreeNode*>[n+1];
}
for(int i = 0; i < n+1; i++) {
dp[i][i].push_back(new TreeNode(i));
}
//find range from i to j
for(int len = 2; len <= n; len++) {
for(int i = 1; i <= n - len +1; i++) {
int j = i + len -1; //find i - j
for(int k = i; k <= j; k++) {
vector<TreeNode*> left = (i > k - 1) ? vector < TreeNode* > {NULL} : dp[i][k - 1];
vector<TreeNode*> right = (k + 1 > j) ? vector < TreeNode* > {NULL} : dp[k + 1][j];
for(int p = 0; p < left.size(); p++) {
for(int q = 0; q < right.size(); q++) {
TreeNode *k_node = new TreeNode(k);
k_node->left = left[p];
k_node->right = right[q];
dp[i][j].push_back(k_node);
}
}
}
}
}
return dp[1][n];
}
};
