介紹

在機器學習（ML）中，通常的關注點是對特定度量進行優化，度量有很多種，例如特定基準或商業 KPI 的分數。為了做到這一點，我們通常訓練一個模型或模型組合來執行目標任務。然後，我們微調這些模型，直到模型的結果不能繼續優化。雖然通常可以通過這種方式使模型達到可接受的效能，但是由於我們的關注點集中在單個任務上，我們忽略了可能幫助優化度量指標的其它資訊。具體來說，這些資訊來自相關任務的訓練訊號。通過共享相關任務之間的表徵，可以使我們的模型更好地概括原始任務。這種方法被稱為多工學習（MTL），這正是本文的主題。

MTL 有很多形式：聯合學習（joint learning）、自主學習（learning to learn）和帶有輔助任務的學習（learning with auxiliary task）等都可以指 MTL。一般來說，優化多個損失函式就等同於進行多工學習（與單任務學習相反）。這些情況有助於你明確地思考如何在 MTL 方面做嘗試並從中獲得啟發。

即使只優化一個損失函式（如在典型情況下），也有可能借助輔助任務來改善原任務模型。Rich Caruana [1] 簡要總結了 MTL 的目標：「MTL 通過利用包含在相關任務訓練訊號中的特定領域的資訊來改進泛化能力」。

在本文中，我將嘗試概括一下多工學習的現狀，特別是當涉及到具有深度神經網路的 MTL 時。我將首先從不同的角度闡述 MTL 的動機。然後，我將介紹 MTL 在深度學習中最常用的兩種方法。隨後，我將描述 MTL 的機制，並闡述為什麼 MTL 在實踐中效果良好。在研究更先進的基於神經網路的 MTL 方法之前，我將通過討論 MTL 的文獻來提供一些背景。然後，我將介紹一些最近提出的更強大的深度神經網路 MTL 方法。最後，我將討論常用的輔助任務型別，並討論什麼是一個好的 MTL 輔助任務。

動機

多工學習的動機有不同的方式：從生物學的角度，多工學習可以看作是受到人類學習的啟發。對於學習新任務，我們經常應用通過學習相關任務獲得的知識。例如，寶寶首先學會識別面部，然後可以應用這些知識來識別其它物件。

從教學的角度，我們經常通過學習任務來獲得必要的技能，以便掌握更復雜的技術。學習武術（比如柔道）的恰當方式也適用於學習程式設計。

以流行文化為例，一個例子是《空手道少年（1984）》（感謝 Margaret Mitchell 與 Adrian Benton 提供靈感）。在電影中，老師宮城先生教導了空手道孩子看起來是無關緊要的任務，如打地板和給車打蠟。事後看來，這些可以讓他掌握與學習空手道相關的寶貴技巧。

最後，從機器學習的角度：我們可以將多工學習看作歸納轉移的一種形式。歸納傳遞可以通過引入歸納偏置（inductive bias）來幫助改進模型，這導致模型比其它模型更喜歡某些假設。例如，一種常見形式的歸納偏置是 L1 正則化，這導致偏好稀疏解。在 MTL 模型下，歸納偏置由輔助任務提供，這導致模型更喜歡假設而不是解釋多個任務。正如我們將在下面看到的，這通常會導致更好的一般化解決方案。

兩種深度學習 MTL 方法

到目前為止，我們只研究了 MTL 的理論動機。為了使 MTL 的思想更具體化，現在我們來看一下在深度神經網路中執行多工學習的兩種最常用的方法。在深度學習中，多工學習通常通過隱藏層的 Hard 或 Soft 引數共享來完成。

Hard 引數共享

共享 Hard 引數是神經網路 MTL 最常用的方法，可以追溯到 [2]。在實際應用中，通常通過在所有任務之間共享隱藏層，同時保留幾個特定任務的輸出層來實現。

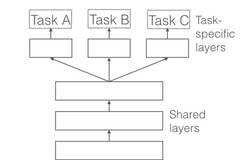
圖 1：深度神經網路多工學習的 Hard 引數共享

共享 Hard 引數大大降低了過擬合的風險。實際上，[3] 表明過擬合共享引數的風險為 O(N)——其中 N 是任務數——小於過擬合特定任務引數，即輸出層。這很直觀：我們同時學習的工作越多，我們的模型找到一個含有所有任務的表徵就越困難，而過擬合我們原始任務的可能性就越小。

Soft 引數共享

另一方面，在共享 Soft 引數時，每個任務都有自己的引數和模型。模型引數之間的距離是正則化的，以便鼓勵引數相似化。例如使用 L2 距離進行正則化 [4]，而 [5] 使用跡範數（trace norm）。

圖 2：深度神經網路多工學習的 Soft 引數共享

約束深度神經網路 Soft 引數共享的思想受到了 MTL 正則化技術的極大啟發，這種思想已經用於其它模型開發，我們將在下面討論。

為什麼 MTL 有效？

即使多工學習獲得的歸納偏置看起來是可信的，為了更好地瞭解 MTL，我們仍需要闡述它所基於的機制。其中大部分最初都是由 Caruana（1998）提出的。對於所有例子，假設我們有兩個相關的任務 A 和 B，它們依賴於一個共同的隱藏層表徵 F。

隱式資料增加

MTL 有效地增加了我們用於訓練模型的樣本大小。由於所有任務不同程度地存在噪聲，當在某些任務 A 上訓練模型時，我們的目標是為任務 A 學習一個很好的表徵，理想情況下，這個表徵能忽略與資料相關的噪聲並具有良好的泛化性。由於不同的任務具有不同的噪聲模式，所以同時學習兩個任務的模型能夠學習更一般的表徵。只學習任務 A 有可能過擬合任務 A，而聯合地學習 A 和 B 使模型能夠通過平均噪聲模式獲得更好的表徵。

注意力機制

如果一個任務非常嘈雜或資料量有限並且高維，模型可能難以區分相關與不相關的特徵。MTL 可以幫助模型將注意力集中在重要的特徵上，因為其它任務將為這些特徵的相關性或不相關性提供額外的證據。

竊聽（eavesdroping）

某特徵 G 很容易被任務 B 學習，但是難以被另一個任務 A 學習。這可能是因為 A 以更復雜的方式與特徵進行互動，或者因為其它特徵阻礙了模型學習 G 的能力。通過 MTL，我們可以允許模型「竊聽」，即通過任務 B 學習 G。最簡單的方法是通過提示（hint）[6]，即直接訓練模型來預測最重要的特徵。

表徵偏置

MTL 任務偏好其它任務也偏好的表徵，這造成模型偏差。這將有助於模型在將來泛化到新任務，因為在足夠數量的訓練任務上表現很好的假設空間也將很好地用於學習具有相同環境的新任務 [7]。

正則化

最後，MTL 通過引入歸納偏置作為正則化項。因此，它降低了過擬合的風險以及模型的 Rademacher 複雜度（即適合隨機噪聲的能力）。

非神經模型中的 MTL

為了更好地瞭解深度神經網路中的 MTL，我們將研究關於 MTL 線上性模型、核函式方法和貝葉斯演算法方面的論文。特別地，我們將討論一直以來在多工學習的歷史中普遍存在的兩個主要思想：通過範數正則化製造各任務間的稀疏性；對任務間的關係進行建模。

請注意，許多 MTL 的論文具有同構性假設：它們假設所有任務與單個輸出相關，例如，多類 MNIST 資料集通常被轉換為 10 個二進位制分類任務。最近的方法更加接近實際，對問題進行異構性假設，即每個任務對應於一組唯一的輸出。

塊稀疏（block-sparse）正則化

為了更好地與下面的方法銜接，我們首先介紹一些符號。我們有 T 個任務。對於每個任務 t，我們有一個模型 m_t，其引數 a_t 的維度是 d。我們可以將引數作為列向量寫出 a_t=[a_{1,t} ... a_{d,t}]^⊤。我們現在逐列地將這些列向量 a_1, ... ,a_T 進行堆疊，形成矩陣 A∈ℝ^{d×T}。A 的第 i 行包含與每個任務的模型的第 i 個特徵對應的引數 a_{i,.}，而 A 的第 j 列包含對應於第 j 個模型的引數 a_{.,j}。

許多現有的方法對模型的引數做了稀疏性假設。例如，假設所有模型共享一小組特徵 [8]。對我們任務的引數矩陣 A 來說，這意味著除了幾行之外，所有資料都是 0，對應於所有任務只共同使用幾個特性。為了實現這一點，他們將 L1 範數推廣到 MTL。回想一下，L1 範數是對引數之和的約束，這迫使除幾個引數之外的所有引數都為 0。這也被稱為 lasso（最小絕對收縮與選擇運算元）。

在單任務中，L1 範數根據相應任務 t 的引數向量 a_t 被計算，在 MTL 中，我們在任務引數矩陣 A 中計算它。為了做到這一點，我們首先對每行 a_i 計算出包含與第 i 個特徵相對應的引數的 Lq 範數，其產生向量 b=[‖a_1‖_q ...‖a_d‖_q]∈ℝ^d。然後，我們計算該向量的 L1 範數，這迫使 b（即 A 矩陣的行）中除少數元素（entry）外，所有元素都為 0。

可以看到，根據我們希望對每一行的約束，我們可以使用不同的 Lq。一般來說，我們將這些混合範數約束稱為 L1/Lq 範數，也被稱為塊稀疏正則化，因為它們導致 A 的整行被設定為 0。[9] 使用 L1/L∞ 正則化，而 Argyriou 等人（2007）使用混合的 L1/L2 範數。後者也被稱為組合 lasso（group lasso），最早由 [10] 提出。

Argyriou 等人（2007）也表明，優化非凸組合 lasso 的問題可以通過懲罰 A 的跡範數（trace norm）來轉化成凸問題，這迫使 A 變成低秩（low-rank），從而約束列引數向量 a_{.,1}，...，a_{.,t} 在低維子空間中。[11] 進一步使用組合 lasso 在多工學習中建立上限。

儘管這種塊稀疏正則化直觀上似乎是可信的，但它非常依賴於任務間共享特徵的程度。[12] 顯示，如果特徵不重疊太多，則 Ll/Lq 正則化可能實際上會比元素一般（element-wise）的 L1 正則化更差。

因此，[13] 通過提出一種組合了塊稀疏和元素一般的稀疏（element-wise sparse）正則化的方法來改進塊稀疏模型。他們將任務引數矩陣 A 分解為兩個矩陣 B 和 S，其中 A=B+S。然後使用 L1/L∞ 正則化強制 B 為塊稀疏，而使用 lasso 使 S 成為元素一般的稀疏。最近，[14] 提出了組合稀疏正則化的分散式版本。

學習任務的關係

儘管組合稀疏約束迫使我們的模型僅考慮幾個特徵，但這些特徵大部分用於所有任務。所有之前的方法都基於假設：多工學習的任務是緊密相關的。但是，不可能每個任務都與所有任務緊密相關。在這些情況下，與無關任務共享資訊可能會傷害模型的效能，這種現象稱為負遷移（negative transfer）。

與稀疏性不同，我們希望利用先驗資訊，指出相關任務和不相關任務。在這種情況下，一個能迫使任務聚類的約束可能更適合。[15] 建議通過懲罰任務列向量 a_{.,1}，...，a_{.,t} 的範數與它們具有以下約束形式的方差來強加聚類約束：

其中

為引數向量的均值。這個懲罰項強制將任務引數向量 a_{.,1}，...，a_{.,t} 向由 λ 控制的均值聚類。他們將此約束應用於核函式方法，但這同樣適用於線性模型。

[16] 也提出了對於 SVM 的類似約束。這個約束受到貝葉斯方法的啟發，並試圖使所有模型接近平均模型。由於損失函式的平衡制約，使每個 SVM 模型的間隔（margin）擴大併產生類似於平均模型的結果。

[17] 在聚類的數量 C 已知的假設下，通過形式化對 A 的約束，使聚類正則化更加明確。然後他們將懲罰項分解為 3 個獨立的範數：

• 衡量列引數向量平均大小的全域性懲罰項：

• 衡量類間距離的類間方差（between-cluster variance）：

其中 T_c 是第 c 個類中任務的數量，是第 c 個類中任務引數向量的均值向量。

• 衡量類內資料緊密度的類內方差（within-cluster variance）：

其中 J(c) 是第 c 個類中任務的集合。

最終的約束形式是這 3 個範數的加權和：

由於此約束假設聚類是已知的，所以它們引入了上述懲罰項的凸鬆弛（convex relaxation），這使演算法允許同時學習聚類。

在另一種情況下，任務可能不在類結構中，但具有其它的結構。[18] 使用擴充套件組合 lasso 來處理樹型結構（tree structure）中的任務，而 [19] 將其應用於具有圖結構（graph structure）的任務。

雖然之前對任務之間關係建模的方法使用了範數正則化，但也存在沒有用到正則化的方法：[20] 第一個提出了使用 k-nn 的任務聚類演算法，而 [21] 通過半監督學習從多個相關任務中學習通用結構。

其它 MTL 任務之間關係的建模使用了貝葉斯方法：

• [22] 提出了使用模型引數先驗的貝葉斯神經網路方法，來鼓勵任務間使用相似的引數。[23] 將高斯過程（Gaussian process/GP）應用於 MTL，該方法利用 GP 推斷共享協方差矩陣的引數。由於這在計算上非常昂貴，它們採用稀疏近似方案用來貪心地選擇資訊量最大的樣本。[24] 同樣將 GP 應用於 MTL，該方法利用 GP 假設所有模型抽樣於同一個普通先驗分佈。

• [25] 在每個任務特定的層上使用高斯分佈作為先驗分佈。為了鼓勵不同任務之間的相似性，他們建議使用任務依賴的平均值，並引入使用混合分佈的任務聚類。重要的是，它們首先需要確定聚類和混合分佈數量的任務特徵。

基於此，[26] 使用 Dirichlet process 提取分佈，並使模型能夠學習任務之間的相似性以及聚類的數量。然後，演算法在同一個類中的所有任務間共享相同的模型。[27] 提出了一個分層貝葉斯模型，它學習一個潛在的任務層次結構，而 [28] 對於 MTL 使用基於 GP 的正則化，並擴充套件以前的基於 GP 的方法，以便在更復雜的設定中增加計算的可行性。

其它方法側重於 on-line 多工學習設定：[29] 將一些現有的方法，如 Evgeniou 等人的方法（2005）應用到 on-line 演算法。他們還提出了一種使用正則化感知機（perceptron）的 MTL 擴充套件方法，該演算法計算任務相關性矩陣。他們使用不同形式的正則化來偏置該任務相關性矩陣，例如，任務特徵向量（characteristic vector）的接近程度或跨度子空間（spanned subspace）的維數。重要的是，與之前的方法類似，它們需要首先確定構成該矩陣的任務特徵。[30] 通過學習任務關係矩陣來擴充套件之前的方法。

[31] 假設任務形成相互分隔的組，並且每個組中的任務位於低維子空間中。在每個組內，任務共享相同的特徵表徵，其引數與組分配矩陣（assignment matrix）一起使用代替的最小化方案學習。然而，組之間的完全分隔可能不是理想的方式，因為任務可能分享一些有助於預測的特徵。

[32] 通過假設存在少量潛在的基礎任務，反過來允許來自不同組的兩個任務重疊。然後，他們將每個實際任務 t 的引數向量 a_t 建模為下面的線性組合：a_t=Ls_t，其中 L∈ℝ^{k×d} 是包含 k 個潛在任務的引數向量的矩陣，而 s_t∈ℝ^k 是包含線性組合係數的向量。此外，它們約束潛在任務中的線性組合為稀疏；約束在稀疏模式下兩個任務之間的重疊然後控制它們之間的共享數量。最後，[33] 學習一個小的共享假設池，然後將每個任務對映到一個假設。

最近 MTL 的深度學習研究

雖然許多最近的深度學習方法已經將多工學習（無論是顯式使用或隱式使用）作為其模型的一部分（例子將在下一節中介紹），但是它們都採用了我們之前介紹的兩種方法，Hard 和 Soft 引數共享。相比之下，只有少數論文研究瞭如何在深度神經網路中開發更優的 MTL 演算法。

深度關係網路

在用於計算機視覺的 MTL 中，通常的方法是共享卷積層，同時學習特定任務的全連線層。[34] 通過提出深度關係網路（Deep Relationship Network）來改進這些模型。除了圖 3 中可以看到的共享和特定任務層的結構之外，他們在全連線層上使用矩陣先驗（matrix priors），這樣可以讓模型學習任務之間的關係，類似於一些之前看過的貝葉斯模型。然而，這種方法仍然依賴於預定義的共享結構，這可能對於已經充分研究的計算機視覺問題是可行的，但是其證明對於新任務來說容易出錯。

圖 3：具有共享卷積和特定任務的全連線層與矩陣先驗的深度關係網路（Long 和 Wang，2015）。

全自適應特徵共享

從另一個極端，[35] 提出了一個從窄網路（thin network）開始的自下而上的方法，並在訓練過程中使用一個促進類似任務分組的標準，貪婪地動態拓寬網路。動態建立分支的拓寬過程可以在圖 4 中看到。但是，貪婪方法可能無法發現全域性最優的模型，而將每個分支正好分配給一個任務不允許模型學習更復雜任務互動。

圖 4：完全自適應特徵共享的拓寬過程（Lu 等人，2016）。

十字繡網路

[36] 從兩個獨立的模型架構開始，如共享 Soft 引數一樣。然後，他們使用稱為十字繡（cross stitch）的單位，以允許模型通過學習前面層的輸出的線性組合來確定如何使特定任務的網路利用其它任務的知識。圖 5 為模型架構，其中它們僅在池化（pooling）和全連線層之後使用十字繡單位。

圖 5：兩個任務的十字繡網路（Misra 等人，2016）。

低監督

相比之下，在自然語言處理（NLP）中，最近的工作側重於為多工學習找到更好的任務層次：[37] 顯示當低階任務用作輔助任務時應該在低層（lower layer）監督，如通常用於預處理的 NLP 任務（如詞性標註/part-of-speech tagging 和命名實體識別/named entity recognition）。

聯合多工模型

基於這一發現，[38] 預定義了由幾個 NLP 任務組成的層次結構，圖 6 為聯合多工學習模型。

圖 6：聯合多工模型（Hashimoto 等人，2016）。

加權損失與不確定性

與學習共享的結構不同，[39] 通過考慮每個任務的不確定性應用正交方法（orthogonal approach）。然後，他們通過基於最大化任務決定的不確定性的高斯似然估計，求導多工損失函式，並以此來調整成本函式中的每個任務的相對權重。每一畫素的深度迴歸（per-pixel depth regression）、語義和例項分割的架構可以在圖 7 中看到。

圖 7：用於多工學習的基於不確定性的損失函式加權（Kendall 等人，2017）。

MTL 的張量因子分解

最近的研究旨在將現有方法泛化到深度學習的 MTL：[40] 概括了一些之前討論的矩陣因子分解的方法，通過使用張量因子分解將每層的模型引數分為共享和特定任務引數。

水閘網路

最後，我們提出了水閘網路（Sluice Network）[41]，一種泛化基於深度學習的 MTL 方法（比如 Hard 引數共享和十字繡網路、塊稀疏正則化方法以及最近的任務層次結構的 NLP 方法）的模型，。圖 8 為該模型，該模型可以學習哪些層和子空間應該共享，以及網路在哪層學到了輸入序列的最佳表徵。

圖 8：兩個任務的水閘網路（Ruder 等人，2017）。

模型應該共享什麼？

在對這些最近的方法進行研究之後，我們現在對深度 MTL 模型中怎樣共享進行簡要總結並得出結論。傳統的大多數 MTL 方法都側重於從相同分佈中抽樣任務（Baxter，1997）。雖然這種情況有利於共享，但並不總是如此。為了開發強大的 MTL 模型，我們必須能夠處理無關或只鬆散相關的任務。

雖然 MTL 早期的深度學習研究已預先指定了為每個任務分配哪些層，但是這一策略並沒有衡量反而嚴重偏差了 MTL 結構。在技術發明 20 年之後，Hard 引數共享（由 Caruana（1997）最初提出）仍然是標準。雖然在許多情況下很有用，但如果任務不緊密相關或需要不同層次的推理，Hard 引數共享就會快速失效。因此，最近的方法正在考慮「學習」分享什麼，並且這個方法通常優於 Hard 引數共享。此外，賦予我們的模型學習任務層次結構的能力是有幫助的，特別是在需要不同粒度的情況下。

正如最初提到的，一旦我們優化了多個損失函式，我們就會做 MTL。與限制模型將所有任務的資訊壓縮到相同的引數空間中不同，基於 MTL 的優勢，我們上面討論的 MTL 的先進演算法是有用的，並使模型能夠了解任務之間是如何互動的。

輔助任務

當我們希望一次獲得多個任務的預測時，MTL 是非常適合的。這種情況在金融或經濟預測中較為常見，我們可能希望預測多種相關指標的值；或者在生物資訊學中同時預測多種疾病的症狀。

然而在大多數情況下，我們只關心一項任務的效果。在本節中，我們將介紹在利用多工學習時如何找到合適的輔助任務。

相關任務

經典的方法是使用相關任務作為 MTL 的輔助任務。為了瞭解相關任務是什麼，我們將介紹一些典型的例子。Caruana（1997）使用多工學習預測自動駕汽車的轉向方向，並將預測道路的不同特徵作為輔助任務；[42] 使用多工學習進行面部特徵點檢測，並將頭姿勢估計和麵部屬性推斷作為輔助任務；[43] 共同學習查詢分類和網頁搜尋；[44] 共同預測影象中物件的類和座標；最後，[45] 共同預測文字到語音的音素持續時間和頻率分佈（frequency profile）。

對抗性

通常，相關任務的標籤資料不可用。然而，在某些情況下，我們想要實現的任務與可用的任務結果相反。可以使用對抗損失函式來利用這些資料，該損失函式不會使用梯度反轉層（gradient reversal layer）來最小化訓練誤差，相反會最大化訓練誤差。這個設定發現最近在域適應方面取得了成功 [46]。在這種情況下的對抗任務是預測輸入的域；通過反轉對抗任務的梯度，使對抗任務的損失函式得到最大化，由於它迫使模型學習不能區分域的表徵，這將有利於主任務。

提示

如前所述，MTL 可用於學習使用原任務不容易學習的特徵。實現這一點的有效方法是使用提示（hint），即將特徵預測為輔助任務。在自然語言處理方面，最近的應用這個方法的例子是 [47]，他們將預測一個輸入句是否包含一個正或負的情感詞作為情感分析（sentiment analysis）的輔助任務，同時，[48] 預測語句中是否存在名字作為名字錯誤檢測的輔助任務。

注意力機制

類似地，輔助任務可用於將注意力集中在網路可能通常忽略的部分影象上。例如，對於學習駕駛（Caruana，1997），單任務模型通常可能忽略車道標記，因為它們僅構成影象的一小部分，而且並不總在圖中出現。然後，將車道標記預測作為輔助任務，強制模型學習它們的表徵；這個資訊也可以用於主任務。類似地，對於面部識別，人們可能會學習將預測面部特徵點的位置作為輔助任務，因為它們通常是獨特的。

量化平滑

對於許多工，訓練目標是量化的，即可用的標籤是離散的，但是連續數值可能更合理。在許多情況下，需要人為評估收集的資料，例如預測疾病（低/中/高）或情感分析（積極/中性/消極）的風險。使用降低量化的輔助任務可能有助於這些情況，由於目標更平滑，它們可能更容易學習。

預測輸入

在某些情況下，使用某些特徵作為輸入是不切實際的，因為它們對預測所需的目標無益。但是，它們仍然可以指導學習任務。在這些情況下，這些特徵可以用作輸出而不是輸入。[49] 提出了這種方法適用的幾種情況。

用未來預測現在

在許多情況下，某些特徵只能在預測之後才能使用。例如，對於自動駕駛汽車，車輛通過後可以進行更準確的障礙物測量和車道標記。Caruana（1997）也給出了肺炎預測的例子，預測後的結果能夠提供額外的醫學試驗結果。對於這些例子，附加資料不能用作特徵，因為它不會在建模時作為輸入使用。然而，它可以用作輔助任務，以便在訓練期間向模型傳入額外的資訊。

表徵學習

MTL 中輔助任務的目標是使模型能夠學習對主任務有共享或有幫助的表徵。迄今為止所討論的所有輔助任務都是隱式的：它們與主任務密切相關，以便幫助模型學習有用的表徵。更顯式的建模是可能的，例如通過採用已知的任務使模型能夠學習可遷移的表徵。Cheng 等人（2015）和 [50] 採用語言模型的目標作為輔助任務。類似地，自編碼器的目標也可以用於輔助任務。

哪些輔助任務是有幫助的？

在本節中，我們討論了可用於 MTL 的不同輔助任務，即使我們只關心一個任務。然而，我們仍然不知道什麼輔助任務在實際中是有用的。尋找輔助任務主要是基於一種假設，即認為輔助任務與主任務有某種相關性，並且有助於預測主任務。

然而，我們仍然不知道什麼時候兩個任務應該被認為是相似或相關的。Caruana（1997）定義如果兩個任務使用相同的特徵作判斷，那麼這兩個任務是相似的。Baxter（2000）認為理論上相關的任務共享一個共同的最優假設類，即具有相同的歸納偏置。[50] 提出，如果兩個任務的資料可以使用一個從一組分佈變換 F 得到的固定概率分佈生成，那麼兩個任務是 F-相關的。雖然這允許對不同感測器收集的相同分類問題的資料的任務進行推理，例如用不同角度和照明條件的相機得到的資料進行物件識別，這不適用於處理不同問題的任務。Xue 等人（2007）討論，如果兩個任務的分類邊界即引數向量接近，則兩個任務是相似的。

在理解任務相關性方面，儘管有這些早期的理論進展，但實踐中還沒有太多進展。任務相似度不是二進位制的，而是在一個頻譜範圍內。MTL 中，更多的相似任務有更大的作用，而較少的相似任務相反。允許我們的模型學習如何分享每個任務，可能使我們能夠暫時避開理論的缺失，並更好利用即使是鬆散相關的任務。然而，我們還需要制定一個有關任務相似性的原則概念，以便了解我們應該選擇哪些任務。

最近的工作 [52] 發現了標籤滿足緊湊且均勻分佈的輔助任務，這適用於 NLP 中的序列標籤問題，並且已經在實驗中（Ruder 等人，2017）得到證實。此外已經發現，主任務更有可能快速達到高峰平穩（plateau），而輔助任務不容易達到高峰平穩 [53]。

然而，這些實驗迄今在範圍上受到限制，最近的發現僅提供了加深對神經網路中多工學習理解的啟發式線索。

結論

在本篇概述中，我們回顧了多工學習的發展歷程，以及最近的深度學習 MTL 的研究。雖然對 MTL 的應用更加頻繁，但是有 20 年曆史的 Hard 引數共享模式仍然普遍存在於神經網路 MTL 中。然而，最新的基於讓模型學習共享引數的方法的進展讓我們看到了希望。同時，我們對任務的理解仍然有限（如，它們的相似性、關係、層次結構和 MTL 的用處），我們需要更多地瞭解它們，以便更好地瞭解 MTL 在深度神經網路方面的泛化能力。