字串匹配就是在一個主串中找到待匹配串的位置，一般是返回第一次出現的位置．一般思路是從待匹配串的第一個字元開始逐個與主串中的字元匹配，如果匹配成功，則主串和待匹配串都後移以為，匹配下一個字元，如果匹配不成功，則主串不動，待匹配串從頭開始匹配．這就是樸素匹配．下面是程式碼

int Index (String S, String T) {
	int i = 1, j = 1;
	while (i <= S.length() && j <= T.length()) {
		if (S[i] == T[j]) {
			++i;
			++j;
		} else {
			i = i - j + 2;
			j = 1;
		}
	}
	if (j > T.length())
		return i - T.length();
	else 
		return 0;
}
//演算法最壞時間複雜度為Ｏ(n*m),n,m分別為主串和待匹配串的長度
 

這種簡單匹配有一個簡單的問題就是，出現大量沒有必要的回退，如
a b a b c a b c a c b a b
．．a b c a c
此時c與b不匹配，帶匹配串要回到第一個字元a處，而主串要回到第二個b處，但是回退後主串和待匹配串此時要匹配的字元肯定不同，這是我們在上一次匹配是就得到的結論，所以這種回退是沒必要的，但怎樣才是回退最少呢？由於此時c與b不匹配，但是c之前的都已經匹配了，假如說主串不動，待匹配串向右滑動，那麼只需要讓待匹配串向右滑動一個距離，使c前面中的字元儘可能多的與主串中的匹配成功，這樣就能使主串回退的少，待匹配串也回退的少．如果這句話沒理解的話，換句話說就是在在主串和待匹配串已經匹配成功的這部分中，挑主串中字尾中與待匹配串字首中相同的部分的最大長度．

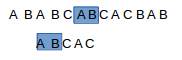
如圖，此時Ｃ與B不匹配，回退就是讓藍色部分儘可能的長，那麼回退的就會少．也就是這部分再次比較了．好了，到這就應該明白我們要幹什麼了，但是怎麼做呢？我們來想想，我們要找的就是不匹配字串之前的那部分已經匹配的部分中，主串的字尾和待匹配串的字首相同的最大部分，而我們要找的這部分所在的部分正好就是已經匹配了的部分，即待匹配串發生不匹配處之前的部分，那麼其實就和主串沒有關係了，只需要在待匹配串的發生不匹配處以前的子串中找到前後綴相同的最大部分就行了．
那好，現在簡單了，只需要分析待匹配串的前後綴就行了，但是是分析誰的前後綴呢，是整個待匹配串的前後綴還是待匹配串的子串的前後綴呢？答案肯定是後者，因為我們每次在發生不匹配時才決定要後退多少步（前後綴相同部分的長度），而不匹配可能在任意一個字元處發生，也就是說，每一個字元都應該對應一個後退值，以便於在發生不匹配是，確定後退多少步．而這個步長我們記錄下來就叫做next值，顧名思義，就是發生不匹配，下一步得後退多少．
那麼next值的求法就是整個演算法的關鍵，這個演算法就是KMP演算法．
那麼next怎麼求呢？如果你之前看過其他文章，肯定會看到一個公式，
$n$

ext[j]={0，當j=1時Max[k∣1<k<j且‘P1...Pk−1=′Pj−k+1...Pj−1′]1，其他情況next[j] = \begin{cases} 0 ，當j=1時\\ Max [k|1 < k < j 且`P1...Pk-1 = 'Pj-k+1...Pj-1']\\ 1，其他情況\\ \end{cases}
首先說明，這是一個很噁心的公式，我TM看不懂．來說說我們該怎麼做吧．
通過剛才的分析，大家應該也已經明白．就是找待匹配串的各個子串的最大公共前後綴長度

求next方法一

找待匹配串中每一個字元前的子串中前後綴最長公共部分

next = 前後綴最長公共部分+1

因為最長公共部分是已經匹配了的，所以要從公共部分的下一個開始比較，而next的值就是下一次比較時開始的位置．
這裡需要注意兩點，
一．待匹配串的第一個字元是不需要回退的，因為它就是回退的最後一個了．
二．子串前後綴沒有重合部分且子串不為空，即需要從子串頭開始匹配，所以next＝１
串在陣列中從下標１開始儲存,所以j從1開始

模式串	A	B	A	B	A	B	B
j	1	2	3	4	5	6	7

這裡說一下什麼是前後綴，字首就是一個字串從前往後，長度小於原串的子串，字尾同理，從後往前．如abcd,字首有a,ab,abc,字尾有d,cd,bcd.

1. 當j=1時發生不匹配，子串為空，next = 0
2. 當j=2時發生不匹配，子串為 A，前後綴公共部分是空， next = 1
3. 當j=3時發生不匹配，子串為 AB，前後綴公共部分為空， next = 1,
4. 當j=4時發生不匹配，子串為 ABA，前後綴公共部分是A， next = 2
5. 當j=5時發生不匹配，子串為 ABAB，前後綴公共部分是AB， next = 3
6. 當j=6時發生不匹配，子串為 ABABA，前後綴公共部分是ABA， next = 4
7. 當j=7時發生不匹配，子串為 ABABAB，前後綴公共部分是ABAB， next = 5

模式串	A	B	A	B	A	B	B
j	1	2	3	4	5	6	7
next	0	1	1	2	3	4	5

求next方法二

1. next[1] = 0, next[2] = 1,
2. k = next[j - 1],
3. 若S[j-1] == S[k] ,則next[j] = k+1;
   若S[j-1] != S[k] , 則 k = next[k];若k != 0,則跳到３，若k 等於 0,next[j] = 1

模式串	A	B	A	B	A	B	B
j	1	2	3	4	5	6	7
next	0	1

1. j = 3, k = next[j-1] = next[2] = 1,
   (S[j-1] = S[2] = B) != (S[k] = S[1] = A),
   k = next[k] = next[1] = 0,
   next[j] = next[3] = 1;
2. j = 4, k = next[j-1] = next[3] = 1,
   (S[j-1] = S[3] = A) == (S[k] = S[1] = A)
   next[j]= next[4] = k+1 = 2
3. j = 5, k = next[j-1] = next[4] = 2,
   (S[j-1] = S[4] = B) == (S[k] = S[2] = B)
   next[j]= next[5] = k+1 = 3
4. j = 6, k = next[j-1] = next[5] = 3,
   (S[j-1] = S[5] = A) == (S[k] = S[3] = A)
   next[j]= next[6] = k+1 = 4
5. j = 7, k = next[j-1] = next[6] = 4,
   (S[j-1] = S[6] = B) == (S[k] = S[4] = B)
   next[j]= next[7] = k+1 = 5

模式串	A	B	A	B	A	B	B
j	1	2	3	4	5	6	7
next	0	1	1	2	3	4	5

void getNext(chat T[], int next[]) {
	int i = 1;
	next[1] = 0;
	int j = 0;
	while (i < T.length()) {
		if (j == 0 || T[i] == T[j]) {
			++i; ++j;
			next[i] = j;
		} else {
			j = next[j];
		}
	}
}

int KMP(char S[], char T[], int next[], int pos) {
	//求T在S中pos位置後的位置
	int i = pos;
	int j= 1;
	while ( i <= S.length() && j <= T.length()) {
		if(j == 0 || S[i] == T[j]) {
			++i;++j;
		} else {
			j = next[j];
		}
	}
	if(j > T.length())
		return i - T.length();
	else
		return 0;
}

KMP 演算法改進

到目前為止我們明白kmp演算法就是在匹配不成功時給我們一個重新開始匹配的位置，以減少比較次數，那看看這種情況

模式串	A	A	A	A	A	B
j	1	2	3	4	5	6
next	0	1	2	3	4	5

如果在j=5是匹配不成功，next[5] = 4,但是S[5] = S[4],也就是演算法給的這個位置還是不能成功匹配，並且next[4] = 3,next[3] = 2…,這樣就要從j=5比較到j=1,但是完全沒有必要，這樣我們就多比了四次，怎麼解決何種問題呢？
其實也很簡單，演算法給我們的next值比不是最後我們想要的位置，也就是next不是最優，原因是前面有大量相同的元素，那麼我們在得到演算法給的next值時，應該再繼續判斷一步，這個next值對應的位置上的值和匹配失敗處的值是否相同，如果不相同，則調到這個next值所在位置，如果相同，那麼繼續判斷下一個next是否相等，依次．．．,所以我們來從新修改next值記為nextval

模式串	A	B	A	B	A	A	B
j	1	2	3	4	5	6	7
next	0	1	1	2	3	4	2

1. j=1, nextval[1] = 0;
2. j=2, S[j] = S[2] = B != S[next[2]] = S[1] = A, nextval[2] = next[2] = 1
3. j=3, S[j] = S[3] = A == S[next[3]] = S[1] = A, 此時先判斷next[next[3]] 是否為0,由於next[next[3]]= 0，所以nextval[3] = 0
4. j=4, S[j] = S[4] = B == S[next[4]] = S[2] = B, next[next[4]] != 0, 繼續判斷S[j] 是否等於S[next[next[4]]], 由於S[j] = S[4] = B ==S[next[next[4]]]= S[1],所以nextval[4] = next[next[4]] = 1
5. j=5, S[5] = A == S[next[5]] = S[3] = A, next[next[5]] = 1,繼續判斷S[5] S[next[next[5]]] = S[1] = A, 繼續判斷，由於next[next[next[5]]]= 0,所以nextval[5]=0,
6. j=6, S[6] = A != S[next[6]] = S[4] = B, nextval[6] = next[6] = 4
7. j=7, S[7] = B == S[next[7]] = S[2] = B, next[next[7]] = 1 != 0,繼續判斷，S[7] = B != S[next[next[7]]] = A, nextval[7] = next[next[7]]=1

模式串	A	B	A	B	A	A	B
j	1	2	3	4	5	6	7
next	0	1	1	2	3	4	2
nextval	0	1	0	1	0	4	1