線性迴歸與邏輯迴歸的區別
阿新 • • 發佈:2018-12-22
線性迴歸
以經典的預測房價為例,
假設樣本為(),其中X是多維變數(),屬性包括房子大小,使用年限等,y是對應該樣本的房價。
那麼我們就可以得到一個預測房價的假設模型,
只要我們求出了引數,就完成了模型的求解,可以用求得的模型來預測新的樣本。
Note:這裡可以看出,這裡求出的模型是一個連續函式,即對應樣本的輸入,輸出會有無限可能(可能為負數,可能為0,也可能為正數,既可能為整數,也可能為浮點數)
邏輯迴歸
同樣以經典的預測房價為例,
假設樣本為(),其中X是多維變數(),屬性包括房子大小,使用年限等,不同的是,這裡的y換成了房價是否超過2萬美元,超過為1,不超過則為0。
於是線性迴歸中的假設模型不能適用到這裡了,需要進行適當的修改。
這裡使用了sigmoid函式對原模型進行修改(在一些教程裡,也有把sigmoid函式叫做邏輯函式的說法),把原模型的輸出規範到了(0, 1)之間。
Note: 這裡可以看出,在使用邏輯迴歸的時候,所預測樣本值的輸出範圍應該是有限的(如0, 1)離散值
這裡可能會有疑問,為什麼不直接用線性迴歸的模型來對這種分類問題進行擬合?
吳恩達的《machine learning》中談到了這點,線性迴歸模型的表達能力有限,如果直接使用線性迴歸,並且使用線性迴歸的平方和作為成本函式,那麼成本函式會變成如下(“non-convex”):
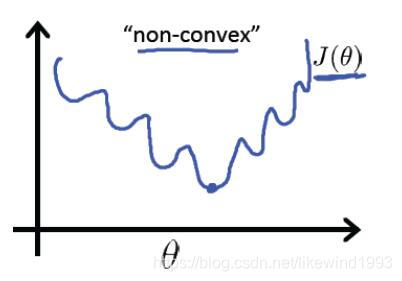
有太多的區域性最優解,如果使用邏輯迴歸並且使用對數損失函式作為成本函式,成本函式才會易於求解(“convex”):

總結
線性迴歸和邏輯迴歸不同的地方有很多,但在我看在,最基本的不同是模型的表示不同,因此導致了所解決問題的能力不同,進而導致了許多的差異。
對這些差異總結如下:
- 邏輯迴歸引入了sigmoid函式,這是一個非線性函式,增加了模型的表達能力
- 邏輯迴歸輸出有限離散值,可以用來解決概率問題、分類問題等。
- 兩者使用的成本函式不同,線性迴歸使用的平方差,邏輯迴歸使用的是對數損失函式(更本質來講,線性迴歸使用最小二乘方法、或梯度下降方法進行成本函式的求解,而邏輯迴歸使用最大似然方法進行求解)
