線性迴歸和邏輯迴歸區別
線性迴歸和邏輯迴歸
線性:y=a*x 是一次方的變化
迴歸:迴歸到平均值
線性迴歸用作迴歸預測
邏輯迴歸用作二分類,也可以做多分類
從資料上來講,線性迴歸的樣本的輸出,都是連續值
邏輯迴歸中y只能取0或者1。
從擬合函式講,線性迴歸:

邏輯迴歸:
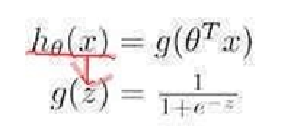
邏輯迴歸實際上就是在多元線性迴歸的基礎之上加了Sigmoid函式。
從公式中可以發現:
線性迴歸的擬合函式實質上是對輸出數值的擬合;
邏輯迴歸的擬合函式實質上是對輸出資料是一類樣本的概率的擬合。
相關推薦
線性迴歸和邏輯迴歸區別
線性迴歸和邏輯迴歸 線性:y=a*x 是一次方的變化 迴歸:迴歸到平均值 線性迴歸用作迴歸預測 邏輯迴歸用作二分類,也可以做多分類 從資料上來講,線性迴歸的樣本的輸出,都是連續值 邏輯迴歸中y只能取0或者1。 從擬合函式講,線性迴歸: 邏輯迴歸: 邏輯迴歸實際上就是在多元線性迴歸
線性迴歸和邏輯迴歸的區別
迴歸問題的條件/前提: 1) 收集的資料 2) 假設的模型,即一個函式,這個函式裡含有未知的引數,通過學習,可以估計出引數。然後利用這個模型去預測/分類新的資料。 1. 線性迴歸 假設 特徵 和 結果 都滿足線性。即不大於一次方。這個是針對 收集的資料而言。 收集的資料中,每一個分量,就
線性迴歸和邏輯迴歸損失函式的區別
首先說什麼是凸函式。對區間[a,b]上定義的函式f,若它對區間中任意兩點x1和x2,均有f((x1+x2)/2)<=(f(x1)+f(x2))/2,則稱f為區間[a,b]上的凸函式。對實數集上的函
機器學習 -- 線性迴歸和邏輯迴歸的區別
迴歸演算法是一種通過最小化預測值與實際結果值之間的差距,而得到輸入特徵之間的最佳組合方式的一類演算法。對於連續值預測有線性迴歸等,而對於離散值/類別預測,我們也可以把邏輯迴歸等也視作迴歸演算法的一種。 線性迴歸與邏輯迴歸是機器學習中比較基礎又很常用的內容。線性迴歸主
【番外】線性迴歸和邏輯迴歸的 MLE 視角
線性迴歸 令 z = w
tensorflow實現線性迴歸和邏輯迴歸
關於線性迴歸和邏輯迴歸的原理和python實現,請左轉:邏輯迴歸、線性迴歸。 這裡就直接貼程式碼了。 線性迴歸: # -*- coding: utf-8 -*- """ Created on Thu Aug 30 09:40:50 2018 @author: 96jie """ im
線性迴歸和邏輯迴歸介紹
概述 線性迴歸和邏輯迴歸是機器學習中最基本的兩個模型,線性迴歸一般用來解決預測問題,邏輯迴歸一般解決分類問題,線性迴歸模型和邏輯迴歸模型之間既有區別又有關聯。 線性迴歸模型 假定訓練資料集為
機器學習演算法總結--線性迴歸和邏輯迴歸
1. 線性迴歸 簡述 在統計學中,線性迴歸(Linear Regression)是利用稱為線性迴歸方程的最小平方函式對一個或多個自變數和因變數之間關係進行建模的一種迴歸分析。這種函式是一個或多個稱為迴歸係數的模型引數的線性組合(自變數都是一次方)。只有一
Python實現線性迴歸和邏輯迴歸演算法
本文使用python實現了線性迴歸和邏輯迴歸演算法,並使用邏輯迴歸在實際的資料集上預測疝氣病症病馬的死亡率(當然這裡我們的線性迴歸和邏輯迴歸實現是原生的演算法,並沒有考慮正則化係數問題,後期會將其補充完整)。 一、線性迴歸 1.模型表示 2.損失函式
線性迴歸和邏輯迴歸的正則化regularization
線性迴歸 介紹 為了防止過度擬合,正則化是一種不錯的思路。能夠使得獲得的邊界函式更加平滑。更好的模擬現實資料,而非訓練樣本。 方法 可以說,regularization是新增懲罰,使得引數接近於零,
【演算法原理】從模型假設看線性迴歸和邏輯迴歸
摘要 本文從演算法的模型假設方面,對線性迴歸、邏輯迴歸和感知器做一下簡要對比,說明了它們之間的聯絡。 符號約定 1)樣本集合: (xi,yi)(1⩽i⩽m)(xi,yi)(1⩽i⩽m),其中ii表示一共mm個樣本中的第ii個 2)xi=(xi0,xi
線性迴歸和邏輯迴歸的比較
線性迴歸 用一組變數的(特徵)的線性組合,來建立與結果之間的關係。 模型表達:y(x,w)=w0+w1x1+...+wnxny(x,w)=w0+w1x1+...+wnxn 邏輯迴歸 邏輯迴歸用於分類,而不是迴歸。 線上性迴歸模型中,輸出一般是連續的
資料探勘從入門到放棄(一):線性迴歸和邏輯迴歸
“ 資料探勘演算法基於線性代數、概率論、資訊理論推導,深入進去還是很有意思的,能夠理解數學家、統計學家、計算機學家的智慧,這個專欄從比較簡單的常用演算法入手,後續研究基於TensorFlow的高階演算法,最好能夠參與到人臉識別和NLP的實際專案中,做出來一定的效果。” 一、理解線性迴歸
線性迴歸、邏輯迴歸和感知機的區別
轉自:https://www.cnblogs.com/muzixi/p/6642203.html寫的很好,但也發現了一些問題嗯,三者在模型,策略(目標函式),演算法(優化方法)上不一樣。一、線性迴歸線性迴歸是一個迴歸問題,即用一條線去擬合訓練資料線性迴歸的模型: 通過訓練資料
線性迴歸與邏輯迴歸的區別
線性迴歸 以經典的預測房價為例, 假設樣本為(X,yiX, y_iX,yi),其中X是多維變數(X=(x1,x2...xn)X = (x_1, x_2...x_n)X=(x1,x2...xn))
線性迴歸與邏輯迴歸的區別與聯絡
logistics本質是線性迴歸,只不過特徵到結果加了一層對映。即先把特徵線性求和,在用Sigmoid函式將結果對映到 [0,1] 如果隨機變數X只取0和1兩個值,並且相應的概率為: 則稱隨機變數X服從引數為p的伯努利分佈,若令q=1一p,則X的概率函式可寫 為:
線性迴歸、邏輯迴歸和softmax方法
線性迴歸(Linear Regression,LR) 對於m個樣本X=[x1,x2⋯xn]TX=[x_{1},x_{2}\cdots x_{n}]^{T}X=[x1,x2⋯xn]T,用引數Θ=[θ1,θ2⋯θn]T\Theta =[\theta _{1}
機器學習——從線性迴歸到邏輯迴歸【附詳細推導和程式碼】
本文始發於個人公眾號:TechFlow,原創不易,求個關注 在之前的文章當中,我們推導了線性迴歸的公式,線性迴歸本質是線性函式,模型的原理不難,核心是求解模型引數的過程。通過對線性迴歸的推導和學習,我們基本上了解了機器學習模型學習的過程,這是機器學習的精髓,要比單個模型的原理重要得多。 新關注和有所遺忘的同
線性迴歸_邏輯迴歸_廣義線性模型_斯坦福CS229_學習筆記
前言 之前學習過視訊版本的吳恩達老師CS229的機器學習課程,但是覺得並不能理解很好。現在結合講義,對於之前的內容再次進行梳理,仍然記錄下自己的思考。圖片來源於網路或者講義。話不多說,進入正題吧。 Part I Regression and Linear Regression
資料學習(1)·線性迴歸和Logistic迴歸
本系列是作者上課時記錄的筆記整理,同時有對應的作業習題,自學的同學參考部落格同步即可。郵箱聯絡[email protected] Preview: 監督學習(第一部分) 線性迴歸 Logistic迴歸 Softmax迴歸
