1、舉例說明

• 定義增量序列D_M > D_M-1 > … > D₁ = 1
• 對每個D_k進行“D_k間隔”排序( k = M, M-1, … 1 )

注意：“D_k間隔”有序的序列，在執行“D_k-1間隔”排序後，仍然是“D_k間隔”有序的

2、原始希爾排序

D_M = [N/2] , D_k = [D_k+1/2]

#include<iostream>
using namespace std;
typedef int ElementType;

void Shell_sort(ElementType A[], int N)
{
	for (int D = N / 2; D >
 
 0; D = D / 2)//希爾增量序列
	{
		for (int i = D; i < N; i++)		//插入排序
		{
			int tmp = A[i];
			int j;
			for (j = i; j >=D && A[j - D]>tmp; j-=D)
				A[j]=A[j-D];
			A[j] = tmp;
		}
	}
}
int main()
{
	int a[] = { 4, 6, 1, 8, 9, 3, 7, 0 };
	int len = sizeof(a) / sizeof(a[0]);
	Shell_sort(a, len);
	for
 
 (int i = 0; i < len; i++)
		cout << a[i] << " ";
	cout << endl;
}

時間複雜度：
最壞情況： T = θ(N²)

O：上界（可能達不到）
Ω ：下界
θ：既是上界又是下界

舉個壞例子：

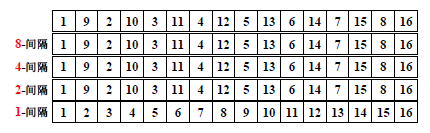
增量元素不互質，則小增量可能根本不起作用。

3、更多增量序列

• Hibbard 增量序列
  • Dk = 2k–1 相鄰元素互質
  • 最壞情況：T=θ(N^3/2)
  • 猜想：Tavg = O(N^5/4)
• Sedgewick增量序列
  • {1, 5, 19, 41, 109, … }
  • 9 * 4ⁱ–9 * 2ⁱ+1 或 4ⁱ
    –3*2ⁱ+1
  • 猜想：Tavg=O(N^7/6)，Tworst=O(N^4/3)