K-Means演算法原理

K-means的優缺點

優點：
1.演算法快速、簡單;
2.對大資料集有較高的效率並且是可伸縮性的;
3.時間複雜度近於線性，而且適合挖掘大規模資料集。K-Means聚類演算法的時間複雜度是O(n×k×t) ,其中n代表資料集中物件的數量，t代表著演算法迭代的次數，k代表著簇的數目

缺點：
1、在k-measn演算法中K是事先給定的，但是K值的選定是非常難以估計的。
2、在 K-means 演算法中，首先需要根據初始聚類中心來確定一個初始劃分，然後對初始劃分進行優化。這個初始聚類中心的選擇對聚類結果有較大的影響，一旦初始值選擇的不好，可能無法得到有效的聚類結果，這也成為 K-means演算法的一個主要問題。
3、當資料量很大時，演算法的開銷是非常大的。

sklearn中的k-means

演算法的目的是選擇出質心，使得各個聚類內部的inertia值最小化，inertial的計算方式如下：

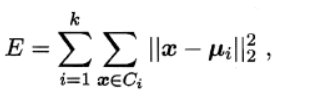
其中ui描述了每個簇的中心（即均值向量）。inertial可以被認為是類內聚合度的一種度量方式。E越小，則簇內樣本相似度越高。

K-means++

從上面的分析可以看出，k-means是隨機的分配k個初始聚類中心。而聚類的結果高度依賴質心的初始化。如果初始聚類中心選的不好，k-means演算法最終會收斂到一個區域性最優值，而不是全域性最優值。為了解決這個問題，引入了k-means++演算法，它的基本思想就是：==初始的聚類中心之間的相互距離要儘可能的遠。==而且在計算過程中，我們通常採取的措施是進行不止一次的聚類，每次都初始化不同的中心，以inertial最小的聚類結果作為最終聚類結果。

sklearn.cluster.KMeans引數介紹

n_clusters：int型，生成的聚類數，預設為8

max_iter：int型，執行一次k-means演算法所進行的最大迭代數。 預設值為300

n_init：int型，用不同的聚類中心初始化值執行演算法的次數，最終解是在inertia意義下選出的最優結果。 預設值為10

init：有三個可選值：‘k-means++’、‘random’、或者傳遞一個ndarray向量。
１）‘k-means++’ 用一種特殊的方法選定初始質心從而能加速迭代過程的收斂
２）‘random’ 隨機從訓練資料中選取初始質心。
３）如果傳遞的是一個ndarray，則應該形如 (n_clusters, n_features) 並給出初始質心。
預設值為‘k-means++’。

tol：float型，預設值= 1e-4　與inertia結合來確定收斂條件。

n_jobs：int型。指定計算所用的程序數。內部原理是同時進行n_init指定次數的計算。
（１）若值為 -1，則用所有的CPU進行運算。若值為1，則不進行並行運算，這樣的話方便除錯。
（２）若值小於-1，則用到的CPU數為(n_cpus + 1 + n_jobs)。因此如果 n_jobs值為-2，則用到的CPU數為總CPU數減1。

random_state：整形或 numpy.RandomState 型別，可選
用於初始化質心的生成器（generator）。如果值為一個整數，則確定一個seed。此引數預設值為numpy的隨機數生成器。

主要屬性

cluster_centers_：聚類中心

labels：每個樣本所屬的簇

inertial_：用來評估簇的個數是否合適，距離越小說明簇分的越好，選取臨界點的簇個數

K值的評估標準

不像監督學習的分類問題和迴歸問題，我們的無監督聚類沒有樣本輸出，也就沒有比較直接的聚類評估方法。但是我們可以從簇內的稠密程度和簇間的離散程度來評估聚類的效果。

1、Calinski-Harabaz Index：越大越好
在sklearn中， Calinski-Harabasz Index對應的方法是sklearn.metrics.calinski_harabaz_score。
CH指標通過計算類中各點與類中心的距離平方和來度量類內的緊密度，通過計算各類中心點與資料集中心點距離平方和來度量資料集的分離度，CH指標由分離度與緊密度的比值得到。從而，CH越大代表著類自身越緊密，類與類之間越分散，即更優的聚類結果。

2、Silhouette Coefficient：輪廓係數（越大越好）
在sklearn中，Silhouette Coefficient對應的方法為sklearn.metrics.silhouette_score。
對於一個樣本點(b - a)/max(a, b)
a平均類內距離，b樣本點到與其最近的非此類的距離。
silihouette_score返回的是所有樣本的該值,取值範圍為[-1,1]。

KMeans演算法實現

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
from sklearn.datasets.samples_generator import make_blobs
from sklearn import metrics
import matplotlib.pyplot as plt

x,y = make_blobs(n_samples=1000,n_features=4,centers=[[-1,-1],[0,0],[1,1],[2,2]],cluster_std=[0.4,0.2,0.2,0.4],random_state=10)

k_means = KMeans(n_clusters=3, random_state=10)

k_means.fit(x)

y_predict = k_means.predict(x)
plt.scatter(x[:,0],x[:,1],c=y_predict)
plt.show()
print(k_means.predict((x[:30,:])))
print(metrics.calinski_harabaz_score(x,y_predict))
print(k_means.cluster_centers_)
print(k_means.inertia_)
print(metrics.silhouette_score(x,y_predict))

[1 1 0 2 1 0 1 1 1 2 1 2 1 1 0 2 1 1 1 0 1 1 0 1 1 1 1 2 0 0]
2672.175134496046
[[-0.98579917 -1.04421422]
 [ 1.4925044   1.49887711]
 [-0.03211515 -0.01417351]]
415.81167375689665
0.5758167373145309