哈夫曼樹

給定n個權值作為n個葉子結點，構造一棵二叉樹，若帶權路徑長度達到最小，稱這樣的二叉樹為最優二叉樹，也稱為哈夫曼樹(Huffman Tree)。哈夫曼樹是帶權路徑長度最短的樹，權值較大的結點離根較近。

樹節點間的邊相關的數叫做權。

從樹中的一個節點到另一個節點之間的分支構成兩個點之間的路徑，路徑上的分支數目稱作路徑長度。

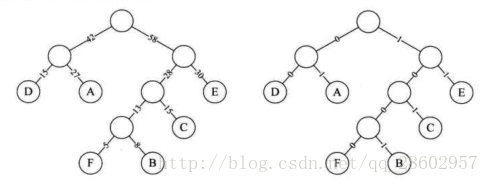
圖中二叉樹a中，跟節點到D的路徑長度就是4，b中根節點到D的路徑長度為2。

樹的路徑長度就是從樹根到每一個節點的路徑長度之和。二叉樹a的路徑長度就為1+1+2+2+3+3+4+4=20。二叉樹b的樹路徑長度就為1+2+3+3+2+1+2+2=16。

如果考慮帶權的節點，節點的帶權的路徑長度就是從該節點到樹根之間的路徑長度乘該節點的權。

數的帶權路徑長度就是所有葉子節點的帶權路徑長度之和。

帶權路徑長度（WPL）最小的二叉樹稱作哈夫曼樹。

如何構造哈夫曼樹

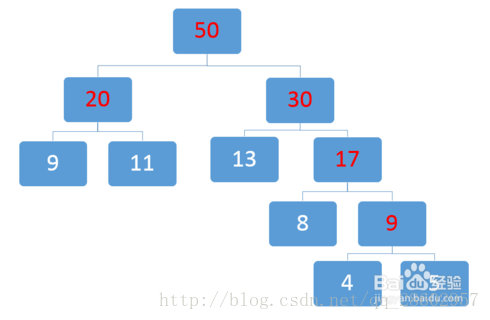
下面我們以【5、8、4、11、9、13】為例來畫出哈夫曼樹（數字大小代表權重大小，越大的權重越大）

第一步：按從小到大排序。

【5、8、4、11、9、13】→【4、5、8、9、11、13】

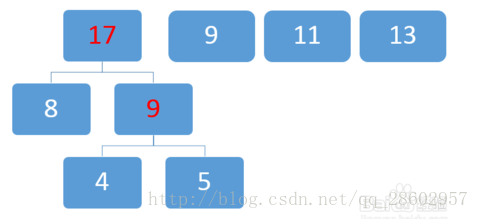
第二步：選最小兩個數畫出一個樹，最小數為4和5。

給定的4、5、8、9、11、13為白色， 紅色的9為4+5，與給定的白9無關，新序列為：【紅9（含子節點4、5）、8、9、11、13】

之後一直重複第一、第二步：排序然後取兩個最小值。實際就是一個遞迴過程

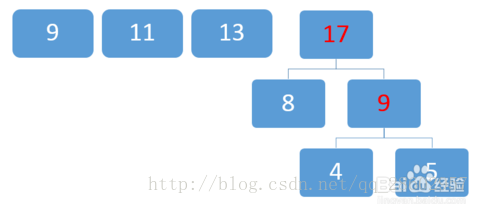
排序：

取兩個最小數8和9：

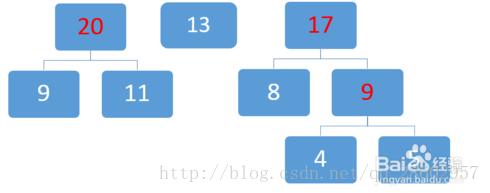
排序：

取兩個最小數9和11：

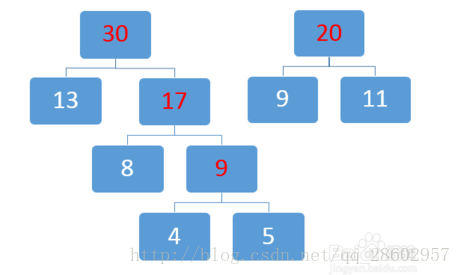
排序，然後取兩個最小數13和17：

取兩個最小數20和30：

哈夫曼編碼

哈夫曼研究這種最優樹的目的是為了解決當年遠距離通訊（主要是電報）的資料傳輸的最優化問題。

比如我們有一段文字“BADCADFEED”，顯然用二進位制數字（0和1）表示是很自然的想法。

這樣真正傳輸的資料就是“001000011010000011101100100011”，對方接收時同樣按照3位一組解碼。如果一篇文章很長，這樣的二進位制串也非常的可怕。而且事實上，每個字母或者漢子的出現頻率是不同的。

假設六個字母的頻率為A 27,B 8, C 15, D 15 , E 30, F 5，合起來正好是100%，那就意味著我們完全可以用哈夫曼樹來規劃它們。

左圖為構造哈夫曼樹的過程的權值顯示。右圖為將權值左分支改為0，右分支改為1後的哈夫曼樹。

我們對這六個字母用其從樹根到葉子所經過的路徑的0或1來編碼，可以得到下表：

也就是說我們的資料被壓縮了，節約了大概17%的儲存或傳輸成本。隨著字元的增加和多字元權重的不同，這種壓縮會更顯出優勢來。

接收到哈夫曼編碼後應該如何解碼呢？

仔細觀察上面的赫夫曼編碼表中各個字母的編碼會發現，不存在容易與1001、1000混淆的10、100等編碼。這就說明若要設計長短不等的編碼，則必須是任一字元的編碼都不是另一個字元的編碼的字首，這種編碼稱作字首編碼。

可僅僅是這樣不足以讓我們去方便的解碼，因此解碼時，還是要用到哈夫曼樹，即傳送方和接收方必須約定好同樣的哈夫曼編碼規則。

下面是赫夫曼編碼的定義：

一般的，設需要編碼的字符集為{d1,d2,…,dn}，各個字元在電文中出現的次數或頻率集合為{w1,w2,…,wn}，以d1,d2,…dn作為葉子結點，以w1,w2,…wn作為相應葉子結點的權值來構造一棵赫夫曼樹。規定赫夫曼樹的左分支代表0，右分支代表1，則從根節點到葉子節點所經過的路徑分支組成的0和1的序列便為該結點對應字元的編碼，這就是赫夫曼編碼。

哈夫曼樹的應用場景

其實赫夫曼樹使用場景還真不少，例如apache負載均衡的按權重請求策略的底層演算法、咱們生活中的路由器的路由演算法、利用哈夫曼樹實現漢字點陣字形的壓縮儲存