【資料結構】可持久化線段樹初步
阿新 • • 發佈:2021-04-02
# 目錄
> 簡介
原理
程式碼
## 簡介
所謂可持久化線段樹,就是將線段樹的各個歷史版本儲存起來,以達到通過利用歷史資訊解決問題的目的。
## 原理
以**權值線段樹**為例,
我們來看看**權值線段樹**是如何實現**可持久化**的。
給出一個**空的**權值線段樹,依次插入四個數:
```
1 3 4 2
```
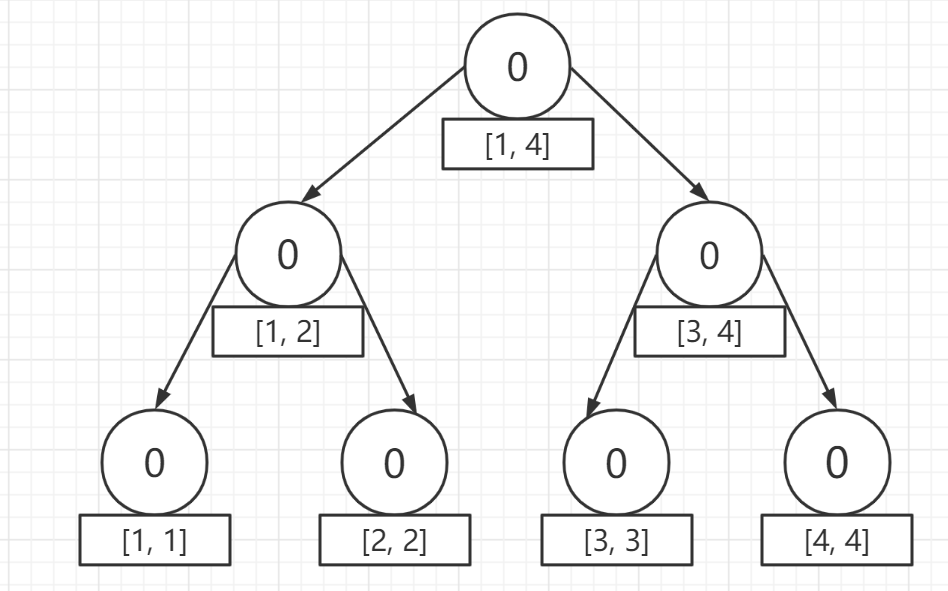
首先,這是空的樹(記為第 $0$ 個版本):(其中鍵值 $cnt$ 表示區間元素個數)
現在插入第一個元素 `1` ,注意到我們要保留每一個歷史版本,所以我們不是在原樹上進行修改,但是我們不可能重新開一個新的線段樹,那麼開銷太大,所以我們發生了修改的地方進行加點:
發生修改的地方:
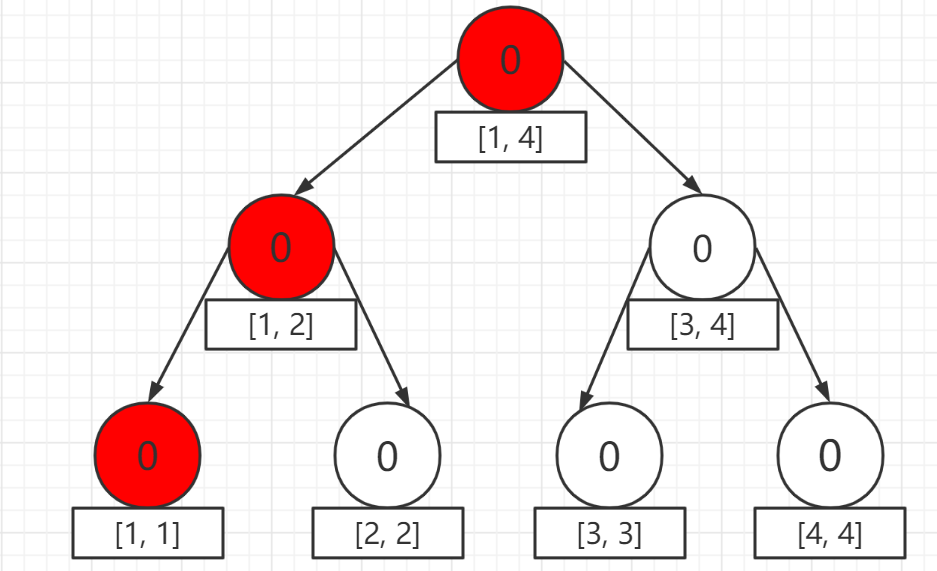
加點:因為這個時候 `1` 的個數為 $1$ ,而且其他結點的元素個數為 $0$ ,所以相關的新增點鍵值 $cnt$ 都是 $1$ 。
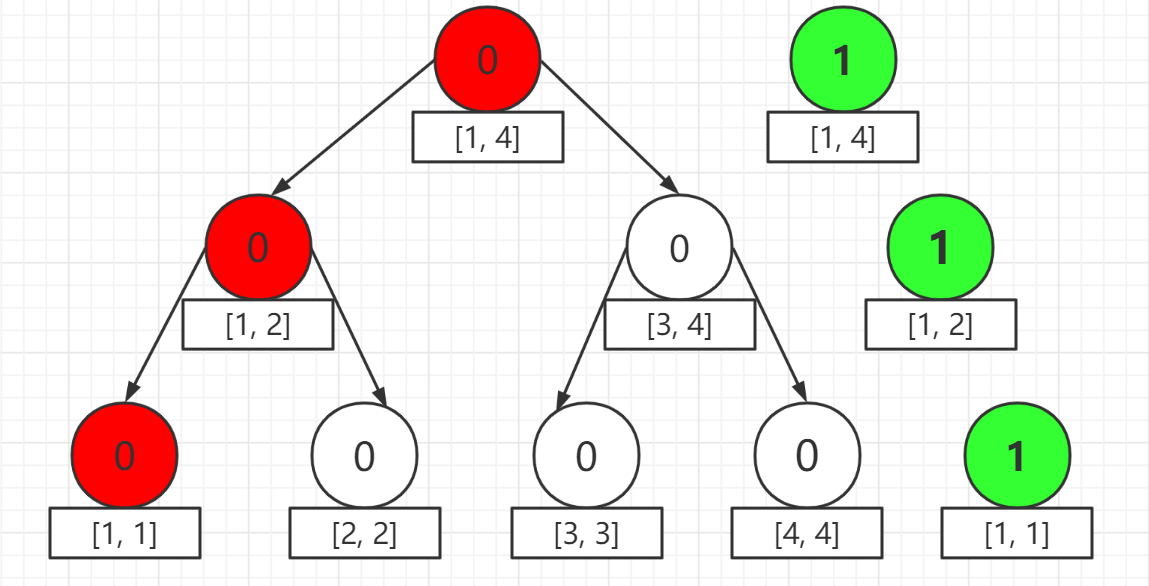
注意到這樣一個事實:新點取代舊點後對應的線段樹結構是完全不變的。
但是舊的節點**並沒有被刪去**。
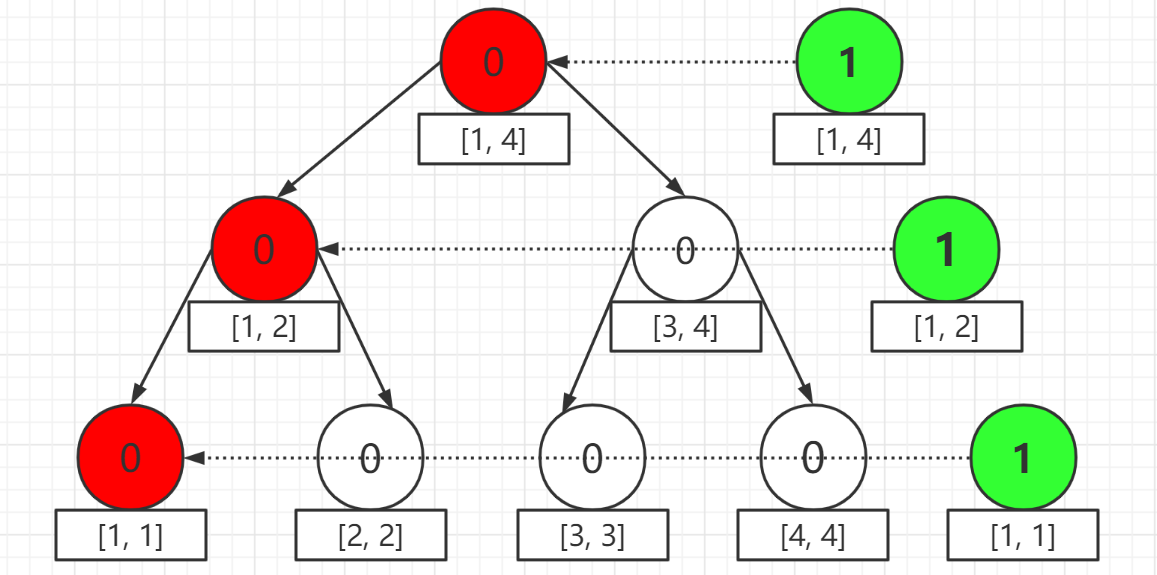
那麼類似地,我們開始插入第二個元素 `3`,每次對於加點只需要基於上一個版本就可以了(紅色結點表示發生修改的點),如圖所示,$cnt$ 也進行相應更新:
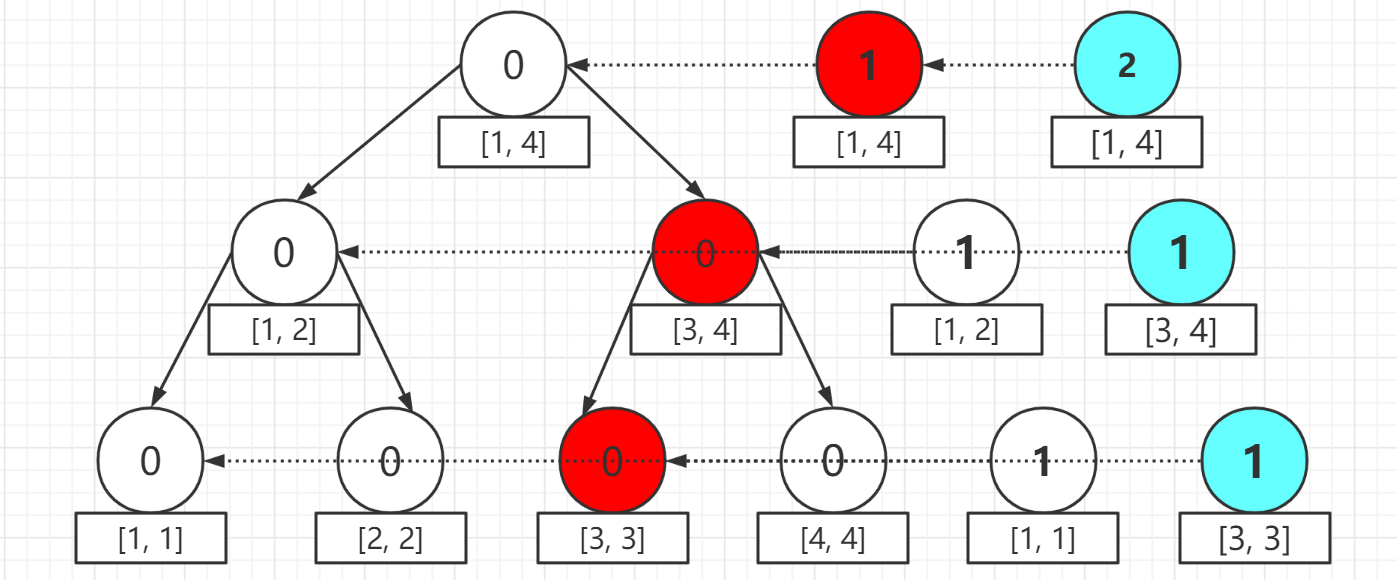
~~是不是有點暈~~,其實到目前,我們有三棵線段樹:
一開始的空樹:
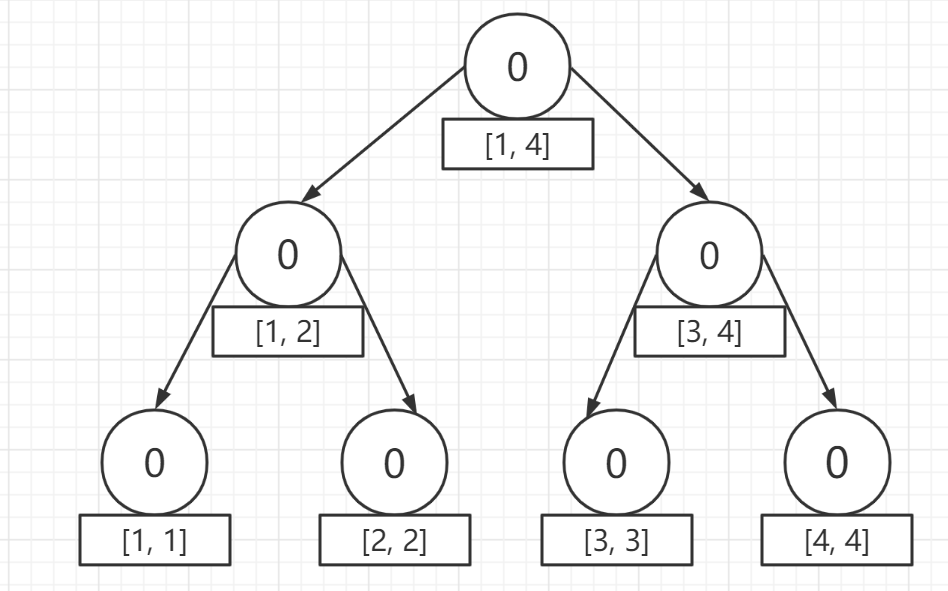
插入第一個元素後得到的第二棵樹:
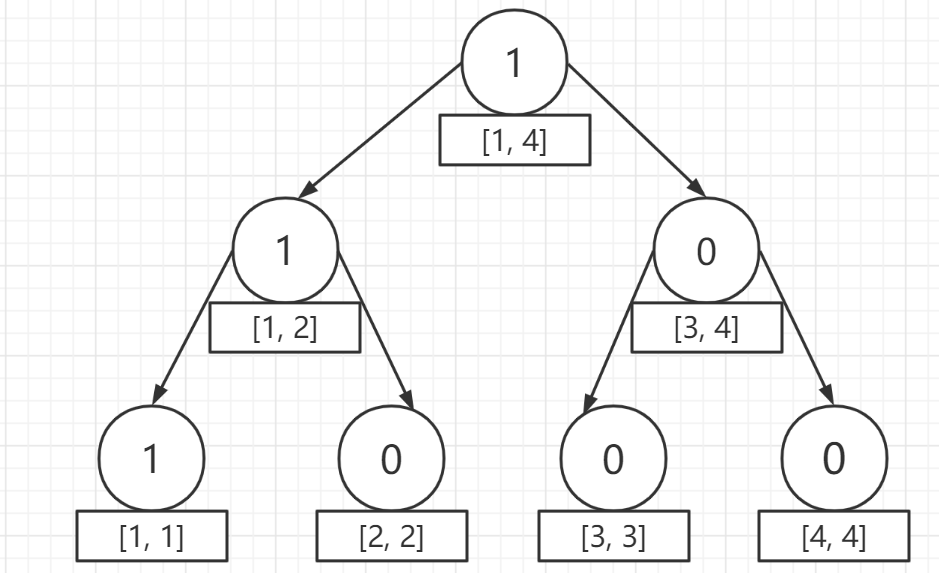
插入第二個元素後得到第三棵樹:
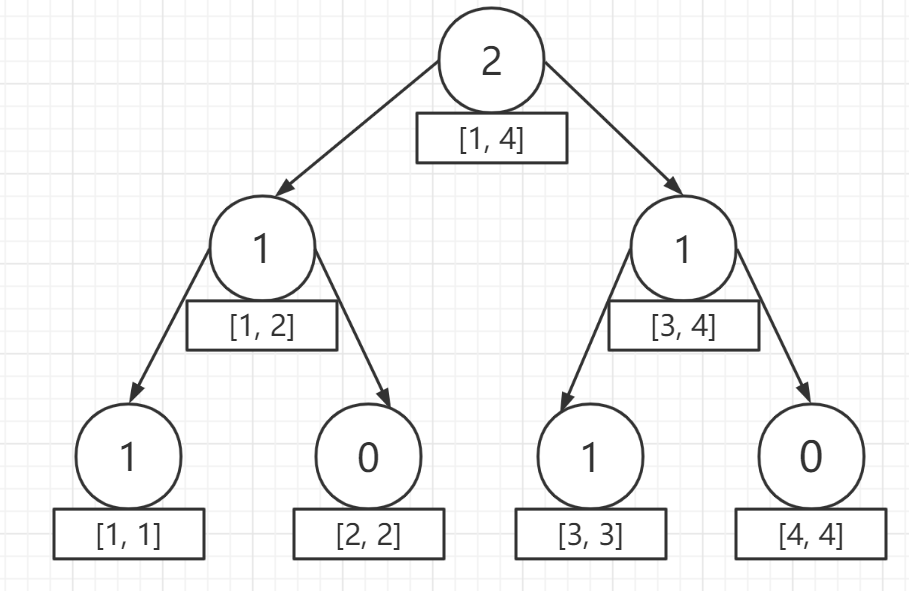
而這三棵樹,都儲存在可持久化線段樹的節點中。
第三第四個元素插入的操作類似於第二個元素插入操作:基於上一版本記錄就好了。
模板題目傳送門:https://www.acwing.com/problem/content/257/
結合模板題進行分析:
如果查詢的區間是 $[1,n]$ ,那麼開一個**權值線段樹**(不妨將它看成一個桶)就可以了,當查詢的 $ k > cnt $ 時,我們向右子樹遞迴,否則向左子樹遞迴。
但是我們需要查詢 $[l,r]$ ,於是使用**可持久化線段樹**來處理:查詢 $[l,r]$ 的 $k$ 小數,基於**字首和的思想**,無非是要知道第 $l-1$ 到 $r$ 次插入操作元素個數的情況,那麼我們作個差就行了:將第 $r$ 個版本對應節點的 $cnt$ 減去 $l-1$ 版本對應節點的 $cnt$ 就能夠獲取相應地元素個數情況了,剩下的操作就是權值線段樹的基本操作,結束。
## 程式碼
```cpp
#include nums; // 離散化
int root[N];
int find(int x){
return lower_bound(nums.begin(),nums.end(),x)-nums.begin();
}
struct node{
int l,r; // 這裡的 l,r 並非區間邊界,而是指向左右兒子結點的編號的指標
int cnt; // 結點鍵值,維護個數。
}tr[4*N+17*N]; // 初始開的點數+logN * N (各版本總規模)
int idx;
// 返回建立的點的編號,兩個引數分別代表左右邊界。
int build(int l,int r){
int u=++idx;
if(l==r) return u;
int mid=l+r>>1;
tr[u].l=build(l,mid), tr[u].r=build(mid+1,r);
return u;
}
// 遞迴地插入
int insert(int p,int l,int r,int x){
int q=++idx;
tr[q]=tr[p];
if(l==r){
tr[q].cnt++;
return q;
}
int mid=l+r>>1;
if(x<=mid) tr[q].l=insert(tr[p].l,l,mid,x); // 如果更新的位置是在左邊,那麼 tr[q].l 為新開點
else tr[q].r=insert(tr[p].r,mid+1,r,x); // 否則 tr[q].r 為新開點
tr[q].cnt=tr[tr[q].l].cnt+tr[tr[q].r].cnt; // pushup the cnt
return q;
}
int query(int p,int q,int l,int r,int k){
if(l==r) return r;
int mid=l+r>
