C++赫夫曼樹的原理和實現
阿新 • • 發佈:2018-12-22
赫夫曼樹的定義
基本概念
(1)節點之間的路徑:一個結點到另一個結點,所經過節點的結點序列。
(2)結點之間的路徑長度:結點之間路徑上的分支數(邊),如汽車到下一站的路徑長度為1。
(3)樹的路徑長度:從根結點到每個葉子結點的路徑長度之和。
(4)帶權路徑: 路徑上加上的實際意義。如汽車到下一站的距離我們叫做權值
(5)樹的帶權路經長度:每個葉子結點到根的路徑長度*權值 之和,記作WPL。
(6)使二叉樹的帶權路徑(WPL)最小的樹 ,我們叫做哈夫曼樹。
赫夫曼樹的構造方法
假設有n個權值,則構造出的哈夫曼樹有n個葉子結點。 n個權值分別設為 w1、w2、…、wn,則哈夫曼樹的構造規則為:
(1) 將w1、w2、…,wn看成是有n 棵樹的森林(每棵樹僅有一個結點);
(2) 在森林中選出兩個根結點的權值最小的樹合併,作為一棵新樹的左、右子樹,且新樹的根結點權值為其左、右子樹根結點權值之和;
(3)從森林中刪除選取的兩棵樹,並將新樹加入森林;
(4)重複(2)、(3)步,直到森林中只剩一棵樹為止,該樹即為所求得的哈夫曼樹。
如:對 下圖中的六個帶權葉子結點來構造一棵哈夫曼樹,步驟如下:
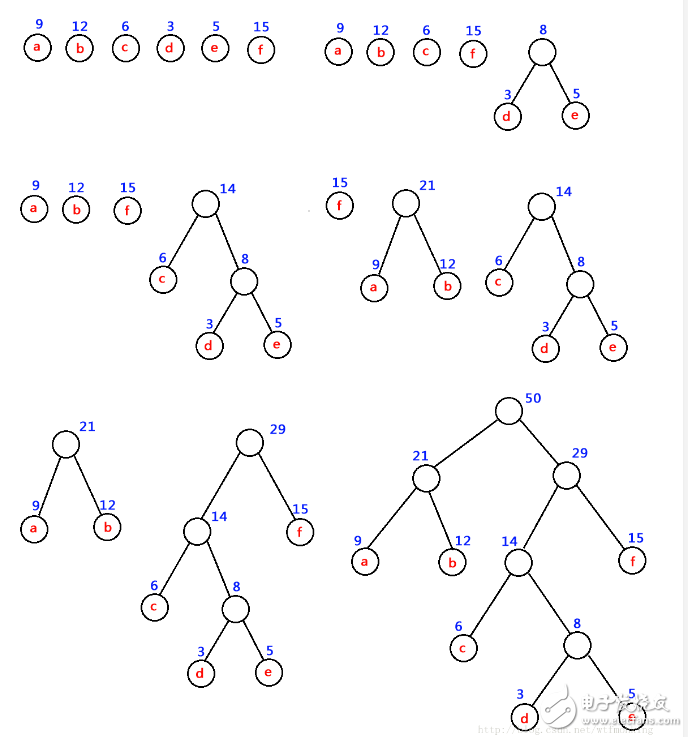
赫夫曼編碼
定義
規定赫夫曼樹的左分支代表0,右分支代表1,則從根結點到葉子結點所經過到路徑分支組成到0和1到序列便為該結點對應字元到編碼。
赫夫曼樹的實現
實現思路
(1).遍歷整個字串,計算出每個字元的出現頻率
(2).將所有的字元的頻率作為權值存在赫夫曼樹結構體中
(3).從所有的赫夫曼樹挑選兩個權重最小的結點並組成新結點,並標記這兩個使用過的結點
(4).重複(3)直到所有結點都已經加入到赫夫曼樹中
(5).根據左子樹為0,右子樹為1,從葉子結點反向計算出赫夫曼編碼
(6).注意!!赫夫曼編碼並不是唯一的,會根據結點在赫夫曼樹中位置不同而改變
實現程式碼
赫夫曼樹的儲存結構
//int佔4個位元組,最大為2147483647
#define MAX 2147483647 (全域性變數)
//代表赫夫曼樹結點的結構體
struct 儲存字元和其出現頻率的結構體
struct LetterFre
{
char ch; //儲存字元
int count; //出現的頻率
};統計字串中字元頻率
//計算每個字元出現的頻率
vector<LetterFre> CntFrequenceOfLetter(string str)
{
vector<LetterFre> InfoList; //儲存字元頻率資訊
if (str.size() == 0)
return InfoList;
sort(str.begin(), str.end());
char s = str[0];
int count = 0;
for (int i = 0; i < str.size(); i++)
{
if (str[i] != s)
{
//將統計的資訊存入結構體
LetterFre letter;
letter.ch = s;
letter.count = count;
InfoList.push_back(letter);
//開始統計下一個字元
s = str[i];
count = 1;
}
else
{
count++;
}
//如果為最後一個字元
if (i == str.size() - 1)
{
//將統計的資訊存入結構體
LetterFre letter;
letter.ch = s;
letter.count = count;
InfoList.push_back(letter);
}
}
return InfoList;
}從結點中找到權重最小的兩個結點的索引
//從森林中選擇權重最小的兩棵樹
void SelectTree(vector<HTNode> *T, int *s1, int *s2)
{
int min = MAX;
//選出第一小的
for (int i = 0; i < T->size(); i++)
{
if ((*T)[i].parent == 0 && (*T)[i].weight <= min)
{
min = (*T)[i].weight;
*s1 = i;
}
}
min = MAX; //MAX為全域性變數
//選出第二小的
for (int i = 0; i < T->size(); i++)
{
if ((*T)[i].parent == 0 && (*T)[i].weight < min && *s1 != i)
{
min = (*T)[i].weight;
*s2 = i;
}
}
}構建赫夫曼樹
//構造赫夫曼樹
vector<HTNode> CrtHuffmanTree(vector<LetterFre> InfoList)
{
vector<HTNode> HTNodeList(InfoList.size());
if (HTNodeList.size() == 0)
return HTNodeList;
else
{
for (int i = 0; i < InfoList.size(); i++)
{
HTNodeList[i].weight = InfoList[i].count;
}
for (int j = InfoList.size(); j < 2 * InfoList.size() - 1; j++)
{
int s1 = 0, s2 = 0;
//找到森林中權重最小的樹
SelectTree(&HTNodeList, &s1, &s2);
//cout << s1 << " " << s2 << endl;
//合併成新結點
HTNode NewNode(HTNodeList[s1].weight + HTNodeList[s2].weight);
NewNode.lchild = s1;
NewNode.rchild = s2;
HTNodeList[s1].parent = HTNodeList.size();
HTNodeList[s2].parent = HTNodeList.size();
HTNodeList.push_back(NewNode);
}
}
return HTNodeList;
}生成赫夫曼編碼
void CrtHuffmanCode(vector<LetterFre> list1, vector<HTNode> list2)
{
vector<int> code;
for (auto i = 0; i < list1.size(); i++)
{
cout << list1[i].ch << ": ";
auto crr = i;
while (list2[crr].parent != 0)
{
auto parent = list2[crr].parent;
if (crr == list2[parent].lchild)
code.push_back(0);
else if (crr == list2[parent].rchild)
code.push_back(1);
crr = list2[crr].parent;
}
//反向遍歷容器
for (auto it = code.rbegin(); it != code.rend(); ++it)
{
cout << *it << " ";
}
cout << endl;
code.clear();
}
}例項
int main()
{
string s = "AAABBBBCCCCCCCCCCDDDDDDDDEEEEEEFFFFF";
auto list = CntFrequenceOfLetter(s);
auto TreeList = CrtHuffmanTree(list);
CrtHuffmanCode(list, TreeList);
/*輸出為
A: 0 0 0
B: 0 0 1
C: 1 0
D: 0 1
E: 1 1 1
F: 1 1 0
*/
}