赫夫曼樹和赫夫曼編碼
問題:根據學生的百分制成績計算5級分製成績,成績在5個等級上的分佈規律:
| 分數 | 0-59 | 60-69 | 70-79 | 80-89 | 90-100 |
| 所佔比例 | 5% | 15% | 40% | 30% | 10% |
樹的路徑長度是從樹根到每一個結點的路徑長度之和。
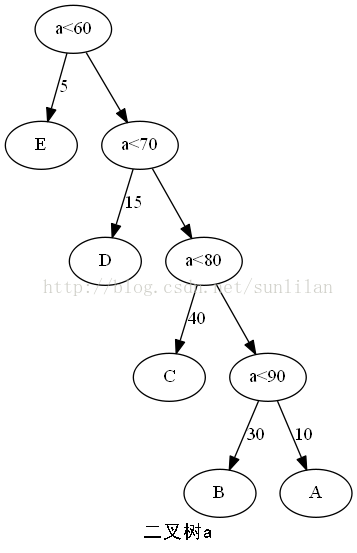
二叉樹a的樹的路徑長度:1+1+2+2+3+3+4+4=20
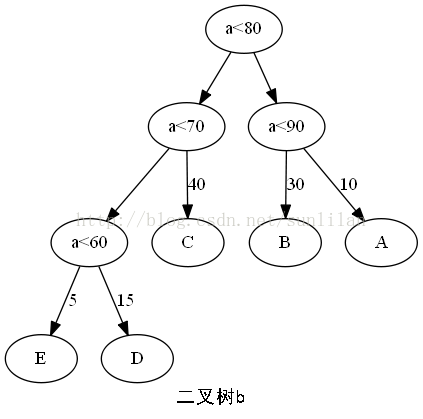
二叉樹b的樹的路徑長度:1+2+3+3+2+1+2+2=16
結點的帶權路徑長度:從樹根到該結點的路徑長度與結點上權的乘積
樹的帶權路徑長度(WPL):樹中所有葉子結點的帶權路徑長度之和。
WPL最小的二叉樹稱為赫夫曼樹二叉樹a的WPL:5×1+15×2+40×3+30×4+10×4=315
這意味著如果有10000個學生的百分制成績需要計算五級分製成績,用二叉樹a的判斷方法,需要31500次比較,而二叉樹b的判斷方法需要22000次比較。
那麼二叉樹b是最優的嗎?赫夫曼樹是如何建立的?
構造赫夫曼樹的演算法:
1.根據給定的n個權值{w1,w2,w3···wn}構成n棵二叉樹的集合F={T1,T2···Tn},其中每個二叉樹Ti中只有一個帶權為Wi的根節點,左右子樹均為空。
2.在F中選取兩棵根節點權值最小的樹作為左右子樹構造一棵新的二叉樹,置二叉樹的根節點的權值為左右子樹上根節點的權值之和。
3.在F中刪除這兩棵樹,同時將新得到的二叉樹加入F中。
4.重複2和3步驟,直到F中只含一棵樹為止。這棵樹是赫夫曼樹。
以上面的問題為例。
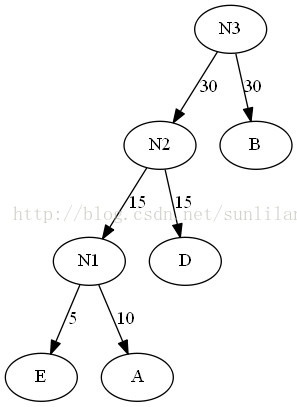
1.列出有權值的葉子結點,排序。E5,A10,D15,B30,C40
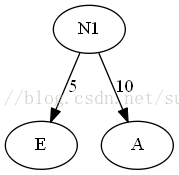
2.選出頭兩個最小權值的結點作為新結點的子結點,注意相對較小的是左結點。新結點的權值為兩個子結點的權值之和。
3.將N1插入有序序列中,刪除A和E。即N1(15),D15,B30,C40
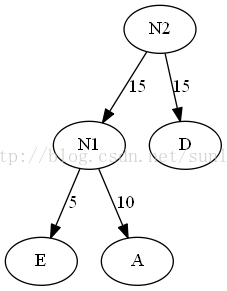
4.重複2。
5.將N2插入有序序列中,刪除N1和D。即N2(30),B30,C40
6.重複2。
7.將N2插入有序序列中,刪除N2和B。即C40,N3(60)
8.重複2。
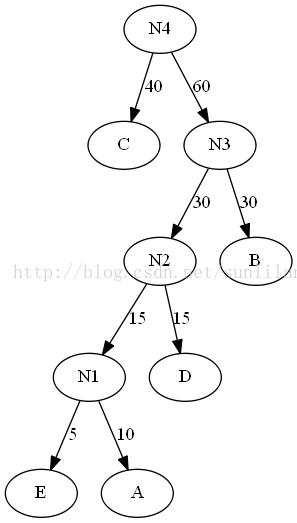
9.將N4插入有序序列,刪除C和N3。此時序列中只含一棵樹,該樹就是赫夫曼樹。
計算這棵樹的WPL:40×1+5×4+10×4+15×3+30×2=205。與之前的二叉樹b的220相比還要小。
不過現實比理想複雜,該赫夫曼樹每次判斷都要兩次比較,比如N4判斷的是a<80&&a>=70,所以總體效能上反而不如二叉樹b。不過這不是我們討論的重點了。
當初研究這種最優樹並不是為了轉化成績的,而是解決遠距離通訊的資料傳輸的最優化問題。
假設我們要傳遞的文字只有6個字母A、B、C、D、E、F。可以按照下表進行編碼。
| 字母 | A | B | C | D | E | F |
| 二進位制字元 | 000 | 001 | 010 | 011 | 100 | 101 |
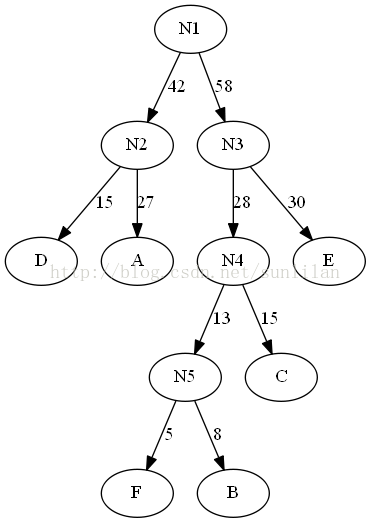
假設六個字母的頻率為A27,B8,C15,D15,E30,F5,合起來是100%。按照赫夫曼樹來規劃。
將樹的左分支的權值改為0,右分支改為1。
可以得到新的編碼規則。
| 字母 | A | B | C | D | E | F |
| 二進位制字元 | 01 | 1001 | 101 | 00 | 11 | 1000 |
對文字內容BADCADFEED編碼
原編碼二進位制串:001000011010000011101100100011
新編碼二進位制串:1001010010101001000111100
所以資料被壓縮了
解碼的時候還要用到赫夫曼樹,即傳送方和接收方必須約定好同樣的赫夫曼編碼規則。
若要設計長短不等的編碼,則必須任一個字元的編碼都不是另一個字元的編碼的字首,這種編碼稱為字首編碼。