2. 程式人生 > >[OI][雜題]NO.1

[OI][雜題]NO.1

阿新 • • 發佈：2018-12-22

NOIP 2015 跳石頭

題目背景

一年一度的“跳石頭”比賽又要開始了!

題目描述

這項比賽將在一條筆直的河道中進行,河道中分佈著一些巨大岩石。組委會已經選擇好了兩塊岩石作為比賽起點和終點。在起點和終點之間,有 N 塊岩石(不含起點和終 點的岩石)。在比賽過程中,選手們將從起點出發,每一步跳向相鄰的岩石,直至到達 終點。

為了提高比賽難度,組委會計劃移走一些岩石,使得選手們在比賽過程中的最短跳 躍距離儘可能長。由於預算限制,組委會至多從起點和終點之間移走 M 塊岩石(不能 移走起點和終點的岩石)。

輸入輸出格式

輸入格式：

輸入檔名為 stone.in。

輸入檔案第一行包含三個整數 L,N,M,分別表示起點到終點的距離,起點和終 點之間的岩石數,以及組委會至多移走的岩石數。

接下來 N 行,每行一個整數,第 i 行的整數 Di(0 < Di < L)表示第 i 塊岩石與 起點的距離。這些岩石按與起點距離從小到大的順序給出,且不會有兩個岩石出現在同 一個位置。

 

輸出格式：

 

輸出檔名為 stone.out。 輸出檔案只包含一個整數,即最短跳躍距離的最大值。

 

輸入輸出樣例

輸入樣例#1： 
25 5 2 
2
11
14
17 
21
輸出樣例#1： 
4

說明

輸入輸出樣例 1 說明：將與起點距離為 2 和 14 的兩個岩石移走後,最短的跳躍距離為 4(從與起點距離 17 的岩石跳到距離 21 的岩石,或者從距離 21 的岩石跳到終點)。

另：對於 20%的資料,0 ≤ M ≤ N ≤ 10。 對於50%的資料,0 ≤ M ≤ N ≤ 100。

對於 100%的資料,0 ≤ M ≤ N ≤ 50,000,1 ≤ L ≤ 1,000,000,000。

------

思路

最短的最長，顯然用二分答案

初始區間[0, L+1)，當跳躍的最短距離設為0的時候，即選手們至少跳0，顯然不需要移走任何一個石頭，因此0可以視為合法的；當跳躍的最短距離設為L+1的時候，顯然選手是無論如何都跳不到這麼長的，因此L+1視為不合法。

因此區間是左閉右開，表示左端點一直是合法的，右端點一直非法的

當前區間[L,R)，二分答案Ans

Ans表示選手跳躍的最短距離

貪心思想：從前往後掃描石頭，模擬選手跳躍的過程，如果能跳（距離大於等於Ans），就跳；不能跳，只能將該石頭搬走

最後總共搬走的石頭數如果小於等於M，表示合法，區間變成[Ans,R)；否則區間變成[L,Ans)

直到區間內沒有數了，答案就是左端點。

code

/*只要最短距離確定了，因為兩端是定的，所以可以確定必須搬走的石塊，因為要求最小值，所以只要把必須搬走的搬走就好了，其他的隨意

所以只需要O(n)列舉一次，使得前i個石頭確定不搬，那麼需要確定第i+1塊石頭怎麼辦，顯然，一旦兩者距離大於了那個最小值就必須把他搬走

所以，時間複雜度是O(nlog(L))*/

#include <cstdio>
#include <cstring>
#define maxn 50005

using namespace std;

int a[maxn],n,m,ans;

bool check(int x) {
    int sum,last;
    sum = 0; last = 0;
    for (int i = 1; i <= n; i++) {
        //能跳就跳，跳不了就移 
        if (a[i] - last < x) {//如果當前石子減去前一個石子（即兩石子間的距離）小於所cheak的跳躍的最短距離
            sum++;//那麼我們就只能將這個石子移走 
            continue;
        }
        last = a[i];//更新last 
    }
    if (sum > m) return false;//如果需要移走的石子總數大於題目最大值
    //假的吧~~ 
    return true; //要不就是真的 
}

int main() {
    int L,R,mid;
    scanf("%d%d%d",&L,&n,&m);
    for (int i = 1; i <= n; i++) 
        scanf("%d",&a[i]);
    n++;
    a[n] = L; R = L; ans = L = 0; 
    while (L <= R) {   
        mid = (L + R) / 2; //好好（瞎）找中點。 
        if (check(mid)) { //二分
            ans = mid; 
            L = mid + 1; //左端點更新 （這裡與下邊右端點的更新都是答案，也就是最短距離的更新） 
        }
        else R = mid - 1; //右端點更新 
    }
    printf("%d",ans);
    return 0;
}

[洛谷] P1736 創意吃魚法

題目描述

回到家中的貓貓把三桶魚全部轉移到了她那長方形大池子中，然後開始思考：到底要以何種方法吃魚呢（貓貓就是這麼可愛，吃魚也要想好吃法 ^_*）。她發現，把大池子視為01矩陣（0表示對應位置無魚，1表示對應位置有魚）有助於決定吃魚策略。

在代表池子的01矩陣中，有很多的正方形子矩陣，如果某個正方形子矩陣的某條對角線上都有魚，且此正方形子矩陣的其他地方無魚，貓貓就可以從這個正方形子矩陣“對角線的一端”下口，只一吸，就能把對角線上的那一隊鮮魚吸入口中。

貓貓是個貪婪的傢伙，所以她想一口吃掉儘量多的魚。請你幫貓貓計算一下，她一口下去，最多可以吃掉多少條魚？

輸入輸出格式

輸入格式：

有多組輸入資料，每組資料：

第一行有兩個整數n和m（n,m≥1），描述池塘規模。接下來的n行，每行有m個數字（非“0”即“1”）。每兩個數字之間用空格隔開。

對於30%的資料，有n,m≤100

對於60%的資料，有n,m≤1000

對於100%的資料，有n,m≤2500

輸出格式：

只有一個整數——貓貓一口下去可以吃掉的魚的數量，佔一行，行末有回車。

輸入輸出樣例

輸入樣例#1： 

4 6 0 1 0 1 0 0

0 0 1 0 1 0

1 1 0 0 0 1

0 1 1 0 1 0

輸出樣例#1：

3 說明

右上角的

1 0 0 0 1 0 0 0 1

code

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>

using namespace std;

inline int read() {
    int num = 0 , f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '0') f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        num = num * 10 + ch - '0';
        ch = getchar();
    }
    return num * f;
}

int n,m,ans;
int map[2510][2510],f[2510][2510],sum1[2510][2510],sum2[2510][2510];

int main() {
    n = read(); m = read();
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) {
            map[i][j] = read();
            if (!map[i][j]) {  
                sum1[i][j] = sum1[i - 1][j] + 1;
                sum2[i][j] = sum2[i][j - 1] + 1;
            }
            else 
                f[i][j] = min(f[i - 1][j - 1],min(sum1[i - 1][j],sum2[i][j - 1])) + 1;
            ans = max(ans,f[i][j]);
        }
    memset(f,0,sizeof(f)); 
    memset(sum1,0,sizeof(sum1)); 
    memset(sum2,0,sizeof(sum2));
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= 1; j--) {
            if (!map[i][j]) {
                sum1[i][j] = sum1[i - 1][j] + 1;
                sum2[i][j] = sum2[i][j + 1] + 1;
            }
            else 
                f[i][j] = min(f[i - 1][j + 1],min(sum1[i - 1][j],sum2[i][j + 1])) + 1;
            ans = max(ans,f[i][j]);
        }
    printf("%d",ans);
    return 0;
}

[ZJOI2005] 午餐

題目描述

上午的訓練結束了，THU ACM小組集體去吃午餐，他們一行N人來到了著名的十食堂。這裡有兩個打飯的視窗，每個視窗同一時刻只能給一個人打飯。由於每個人的口味（以及胃口）不同，所以他們要吃的菜各有不同，打飯所要花費的時間是因人而異的。另外每個人吃飯的速度也不盡相同，所以吃飯花費的時間也是可能有所不同的。

THU ACM小組的吃飯計劃是這樣的：先把所有的人分成兩隊，並安排好每隊中各人的排列順序，然後一號隊伍到一號視窗去排隊打飯，二號隊伍到二號視窗去排隊打飯。每個人打完飯後立刻開始吃，所有人都吃完飯後立刻集合去六教地下室進行下午的訓練。

現在給定了每個人的打飯時間和吃飯時間，要求安排一種最佳的分隊和排隊方案使得所有人都吃完飯的時間儘量早。

假設THU ACM小組在時刻0到達十食堂，而且食堂裡面沒有其他吃飯的同學（只有打飯的師傅）。每個人必須而且只能被分在一個隊伍裡。兩個視窗是並行操作互不影響的，而且每個人打飯的時間是和視窗無關的，打完飯之後立刻就開始吃飯，中間沒有延遲。

現在給定N個人各自的打飯時間和吃飯時間，要求輸出最佳方案下所有人吃完飯的時刻。

輸入輸出格式

輸入格式：

 

第一行一個整數N，代表總共有N個人。

以下N行，每行兩個整數 Ai，Bi。依次代表第i個人的打飯時間和吃飯時間。

 

輸出格式：

 

一個整數T，代表所有人吃完飯的最早時刻。

 

輸入輸出樣例

輸入樣例#1：  
5
2 2
7 7
1 3
6 4
8 5
輸出樣例#1：  
17

說明

所有輸入資料均為不超過200的正整數。

 ------

思路

為了簡化問題，我們先來考慮一對怎麼搞

首先，我們需要一個順序。也就是劃分階段

類似於排隊接水的順序，但需要換一個角度思考

由於每個人打完飯就跑路開吃，所以所有人總共要打飯的時間是固定的，就是把所有人的打飯時間加起來

那麼我們考慮，如果僅有兩人AB，他們的打飯時間和吃飯時間都不同，是A在前快還是B在前快？

畫個圖就知道，很明顯是吃飯時間長的排在前面比較快。

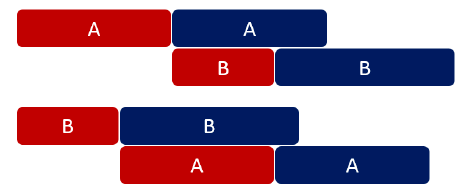
for(int i = 1; i <= n; ++ i)
    cin >> a[i] >> b[i], p[i] = i;
sort(p+1, p+n+1, cmp); // 按照吃飯時間排序

得到這個結論後，就可以搞DP了

對於每個人，我們考慮是去第一隊還是第二隊兩種情況

用f[i]表示考慮到第i 個人, 目前最優的吃飯時間

狀態補充一下，用f[i][j][k]表示第一條隊總時長為j, 第二條隊總時長為k

到這裡DP就差不多了

但是我們發現

三維陣列造成了很大的空間開銷

能不能陣列壓縮為二維陣列呢？

在考慮順序時我們說過，總的排隊時間是不變的

也就是說，如果知道在一隊的全部人，那麼我們也就知道了在二隊的全部人，因為二隊人的排隊時間和等於總和減去一隊人的排隊時間和

f[i+1][j+A] = min(f[i+1][j+A], max(f[i][j], j+A+B)); // 排第一條隊
f[i+1][j] = min(f[i+1][j], max(f[i][j], s[i-1]-j+A+B)); // 排第二條隊

只需要在DP前搞一下字首和就好了

for(int i = 1; i <= n; ++ i) // 求字首和
    s[i] = s[i-1] + a[p[i]];

這樣我們就可以用二維陣列解決掉這道題

當然你也可以用兩個不同的陣列表示一隊和二隊

這裡不再贅述。

code

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>

using namespace std;

const int N = 205;
const int M = N * N;
const int INF = 1e9;

int n, f[N][M], sum[N]; 

struct Edge {
    int A, B;
}T[N];

bool cmp(Edge x, Edge y) { return x.B > y.B;}

int main() {
    scanf("%d", &n); 
    for (int i = 1; i <= n; i++) 
        scanf("%d%d",&T[i].A, &T[i].B);
    sort(T + 1, T + n + 1, cmp);
    for (int i = 1; i <= n; i++) 
        sum[i] = sum[i-1] + T[i].A;
    int m = n * N;
    for(int i = 1; i <= n + 1; i++) 
        for(int j = 0; j <= m; j++) f[i][j] = INF;
    f[1][0] = 0; 
    for (int i = 1; i <= n; i++) 
        for (int j = 0; j <= m; j++) 
            if (f[i][j] < INF) {
                f[i+1][j+T[i].A] = min(f[i+1][j+T[i].A], 
　　　　　　　　　　　　max(f[i][j], j + T[i].A + T[i].B));
                f[i+1][j] = min(f[i+1][j], 
　　　　　　　　　　　　max(f[i][j], sum[i-1] - j + T[i].A + T[i].B));
            }
    int ans = INF;
    for(int i = 0; i <= m; i++) ans = min(ans, f[n+1][i]);
    printf("%d", ans);
    return 0;
}

P3701 「偽模板」主席樹

題目背景

byx和手氣君都非常都非常喜歡種樹。有一天，他們得到了兩顆奇怪的樹種，於是各自取了一顆回家種樹，並約定幾年後比一比誰種出來的樹更加牛x。

題目描述

很快，這棵樹就開花結果了。byx和手氣君驚訝的發現，這是一棵主席樹，樹上長滿了主席和主席的朋友們。這棵樹上一共有五種人，主席(J)，記者(HK)，高人(W)，女王(E)和膜法師(YYY)。他們發現，他們的主席樹上的人數相同，都為N。

 

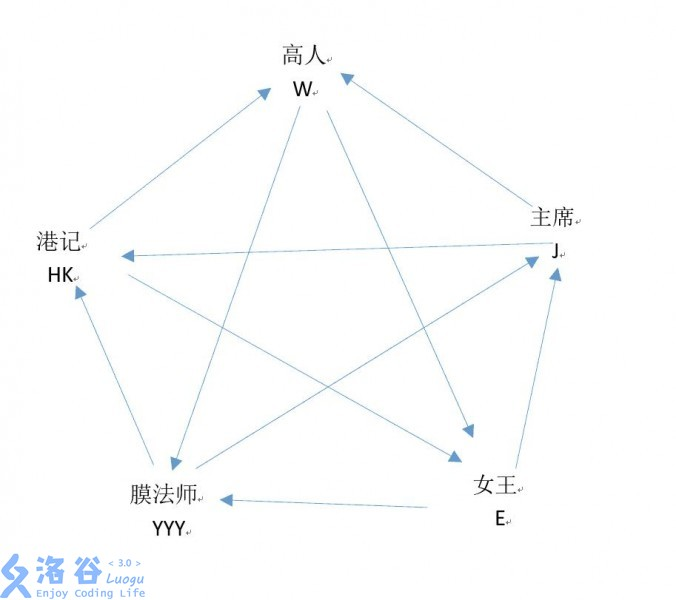
研究發現，這五種人的輸贏如上圖所示（一樣的人不能PK），箭頭指向輸的人。至於為什麼，留給同學們自己思考。

比賽如期進行。

byx和手氣君要進行M場比賽，每一場比賽他們會選出樹上的兩個人來比較看誰更牛x。

第i個人壽命為Lifei秒，每次比完賽他們就會-1s。當他們生命為0s時他們就不能再比賽了。

同時，當J的壽命為0時，同一棵樹上的YYY可以為他+1s。每個YYY只能給.每個J續一次。

那麼問題來了

現在給定N,M（1≤N≤100,1≤M≤1000），A和B每一個人所屬種類(J,HK,W,YYY或E)以及每一個人的生命，生命不超過50.請你算算A最多能夠贏得多少場比賽呢。

資料保證每一場一定都有人用。兩個人之間只能比一場。

輸入輸出格式

輸入格式：

第一行包含兩個數N,M，含義看上面。

第二行N個字串(J,HK,W,YYY或E)，表示byx的人所屬種類，用空格隔開。

第三行N個字串(J,HK,W,YYY或E)，表示手氣君的人所屬種類，用空格隔開。

第四行N個數，表示byx的人的生命。

第五行N個數，表示手氣君的人的生命。

輸出格式：

一個數，byx能贏的場次

輸入輸出樣例

輸入樣例#1：  
3 3
J W YYY
J HK E
2 2 2
2 2 2
輸出樣例#1：  
3

說明

第一場主席贏記者，第二場高人贏女王，第三場膜法師贏記者。

------

思路

標題都是騙人的

本來還以為是主席樹……看了題面發現是網路流……

覺得發現了一道極水的黑題

但是調了2個多小時……

為什麼呢？

    for (R int i = 1 + n; i <= 2 * n; ++ i) 
        AddEdge(i, T, hp2[i]), AddEdge(T, i, 0);
    for (R int i = 1; i <= n; ++ i) 
        AddEdge(i + n, T, hp2[i]), AddEdge(T, i + n, 0);

這兩句……有區別嗎？

但是第一個就是輸出0啊

R是register……去掉也不管用……

為啥？為啥？為啥？

這種玄學錯誤我還能調出來真的是謝天謝地了

求大佬解惑

code

#include <algorithm>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <iostream>
#include <map>
#include <queue>
#define R register

typedef long long ll;
typedef double db;
const int INF = 1e9;
const int MAXM = 10010;
int n, m, hp1[110], hp2[110];
char name1[110][3], name2[110][3];
int ecnt = 1, head[MAXM], dep[MAXM];

struct Edge {
    int to, nxt, ret;
}e[MAXM];

inline int read() {
    int num = 0, f = 1; char ch = getchar();
    while (!isdigit(ch)) {if (ch == '-') f = -1; ch = getchar();}
    while (isdigit(ch)) {num = num * 10 + ch - '0'; ch = getchar();}
    return num * f;
}

void AddEdge(int x, int y, int c) {
    e[++ ecnt].to = y; e[ecnt].ret = c; 
    e[ecnt].nxt = head[x]; head[x] = ecnt;
}

int dfs(int x, int t, int maxFlow) {
    if (!maxFlow || x == t) return maxFlow;
    int ans = 0, v, f;
    for (int i = head[x]; i; i = e[i].nxt) {
        v = e[i].to;
        if (dep[v] == dep[x] + 1 && e[i].ret > 0) {
            f = dfs(v, t, std::min(maxFlow - ans, e[i].ret));
            e[i].ret -= f;
            e[i ^ 1].ret += f;
            ans += f;
        }
    }
    if (ans < maxFlow) dep[x] = n + 1;
    return ans;
}

bool bfs(int s, int t) {
    std::queue<int> q;
    memset(dep, -1, sizeof(dep));
    q.push(s);
    dep[s] = 0;
    int h, v;
    while (!q.empty()) {
        h = q.front(); q.pop();
        for (int i = head[h]; i; i = e[i].nxt) {
            v = e[i].to;
            if (e[i].ret > 0 && dep[v] == -1) {
                q.push(v);
                dep[v] = dep[h] + 1;
            }
        }
    } return dep[t] != -1;
}

int Dinic(int s, int t) {
    int ans = 0;
    while (bfs(s, t)) ans += dfs(s, t, INF);
    return ans;
}

int main() {
    n = read(), m = read();
    //std::cin >> n >> m;
    int add1 = 0, add2 = 0;
    for (R int i = 1; i <= n; ++ i) {
        scanf("%s", name1[i]);
        if (name1[i][0] == 'Y') ++ add1;
    }
    for (R int i = 1; i <= n; ++ i) {
        scanf("%s", name2[i]);
        if (name2[i][0] == 'Y') ++ add2;
    }
    for (R int i = 1; i <= n; ++ i) {
        hp1[i] = read();
        //std::cin >> hp1[i];
        if (name1[i][0] == 'J') hp1[i] += add1;
    }
    for (R int i = 1; i <= n; ++ i) {
        hp2[i] = read();
        //std::cin >> hp2[i];
        if (name2[i][0] == 'J') hp2[i] += add2;
    }
    int S = 0, T = 2 * n + 1;
    for (R int i = 1; i <= n; ++ i) 
        AddEdge(S, i, hp1[i]), AddEdge(i, S, 0);
    /*for (R int i = 1 + n; i <= 2 * n; ++ i) 
        AddEdge(i, T, hp2[i]), AddEdge(T, i, 0);*/
    for (R int i = 1; i <= n; ++ i) 
        AddEdge(i + n, T, hp2[i]), AddEdge(T, i + n, 0);
    for (R int i = 1; i <= n; ++ i) for (R int j = 1; j <= n; ++ j) {
        if (name1[i][0] == 'J' && (name2[j][0] == 'W' || name2[j][0] == 'H'))
            AddEdge(i, j + n, 1), AddEdge(j + n, i, 0);
        if (name1[i][0] == 'W' && (name2[j][0] == 'Y' || name2[j][0] == 'E'))
            AddEdge(i, j + n, 1), AddEdge(j + n, i, 0);
        if (name1[i][0] == 'H' && (name2[j][0] == 'W' || name2[j][0] == 'E'))
            AddEdge(i, j + n, 1), AddEdge(j + n, i, 0);
        if (name1[i][0] == 'E' && (name2[j][0] == 'Y' || name2[j][0] == 'J'))
            AddEdge(i, j + n, 1), AddEdge(j + n, i, 0);
        if (name1[i][0] == 'Y' && (name2[j][0] == 'H' || name2[j][0] == 'J'))
            AddEdge(i, j + n, 1), AddEdge(j + n, i, 0);
    }    
    std::cout << std::min(Dinic(S, T), m) << std::endl;
    return 0;
}

QwQ無力吐槽

P3431 [POI2005]AUT-The Bus

題目描述

The streets of Byte City form a regular, chessboardlike network - they are either north-south or west-east directed. We shall call them NS- and WE-streets. Furthermore, each street crosses the whole city. Every NS-street intersects every WE- one and vice versa. The NS-streets are numbered from 111 to nnn , starting from the westernmost. The WE-streets are numbered from 111 to mmm , beginning with the southernmost. Each intersection of the iii 'th NS-street with the jjj 'th WE-street is denoted by a pair of numbers (i,j)(i,j)(i,j) (for 1≤i≤n1\le i\le n1≤i≤n , 1≤j≤m1\le j\le m1≤j≤m ).

There is a bus line in Byte City, with intersections serving as bus stops. The bus begins its itinerary by the (1,1)(1,1)(1,1) intersection, and finishes by the (n,m)(n,m)(n,m) intersection. Moreover, the bus may only travel in the eastern and/or northern direction.

There are passengers awaiting the bus by some of the intersections. The bus driver wants to choose his route in a way that allows him to take as many of them as possible. (We shall make an assumption that the interior of the bus is spacious enough to take all of the awaiting passengers, regardless of the route chosen.)TaskWrite a programme which:

reads from the standard input a description of the road network and the number of passengers waiting at each intersection,finds, how many passengers the bus can take at the most,writes the outcome to the standard output.

Byte City 的街道形成了一個標準的棋盤網路 – 他們要麼是北南走向要麼就是西東走向. 北南走向的路口從 1 到 n編號, 西東走向的路從1 到 m編號. 每個路口用兩個數(i, j) 表示(1 <= i <= n, 1 <= j <= m). Byte City裡有一條公交線, 在某一些路口設定了公交站點. 公交車從 (1, 1) 發車, 在(n, m)結束.公交車只能往北或往東走. 現在有一些乘客在某些站點等車. 公交車司機希望在路線中能接到儘量多的乘客.幫他想想怎麼才能接到最多的乘客.

輸入輸出格式

輸入格式：

The first line of the standard input contains three positive integers nnn , mmm and kkk - denoting the number of NS-streets, the number of WE-streets and the number of intersections by which the passengers await the bus, respectively ( 1≤n≤1091\le n\le 10^91≤n≤109 , 1≤m≤1091\le m\le 10^91≤m≤109 , 1≤k≤1051\le k\le 10^51≤k≤105 ).

The following kkk lines describe the deployment of passengers awaiting the bus, a single line per intersection. In the (i+1)(i+1)(i+1) 'st line there are three positive integers xix_ixi​ , yiy_iyi​ and pip_ipi​ , separated by single spaces, 1≤xi≤n1\le x_i\le n1≤xi​≤n , 1≤yi≤m1\le y_i\le m1≤yi​≤m , 1≤pi≤1061\le p_i\le 10^61≤pi​≤106 . A triplet of this form signifies that by the intersection (xi,yi)pi(x_i,y_i)p_i(xi​,yi​)pi​ passengers await the bus. Each intersection is described in the input data once at the most. The total number of passengers waiting for the bus does not exceed 1 000 000 0001\ 000\ 000\ 0001 000 000 000 .

輸出格式：

Your programme should write to the standard output one line containing a single integer - the greatest number of passengers the bus can take.

輸入輸出樣例

輸入樣例#1：  
8 7 11
4 3 4
6 2 4
2 3 2
5 6 1
2 5 2
1 5 5
2 1 1
3 1 1
7 7 1
7 4 2
8 6 2
輸出樣例#1： 

11

------

日常DP

code

#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <vector>
#define R register

const int MAXN = 100010;

int n, m, k;
int b[MAXN], f[MAXN], ans, cnt;

struct POS{
    int x, y, num;
    bool operator < (const POS &t) const {
        if (x == t.x) return y < t.y;
        return x < t.x;
    }
}p[MAXN];

inline int read() {
    int num = 0, f = 1; char ch = getchar();
    while (!isdigit(ch)) {if (ch == '-') f = -1; ch = getchar();}
    while (isdigit(ch)) {num = num * 10 + ch - '0'; ch = getchar();}
    return num * f;
}

int t[MAXN];
int Lowbit(int x) {return x&(-x);}
void Update(int x, int k) {while(x<=cnt)t[x]=std::max(t[x],k),x+=Lowbit(x);}
int Query(int x) {int d=0;while(x>0)d=std::max(d,t[x]),x-=Lowbit(x);return d;}

int main() {
    n = read(); m = read(); k = read();
    for (R int i = 1; i <= k; ++ i) {
        p[i].x = read(), p[i].y = read(), p[i].num = read();
        b[i] = p[i].y;
    }
    std::sort(b + 1, b + k + 1);
    cnt = std::unique(b + 1, b + k + 1) - (b + 1);
    for (R int i = 1; i <= k; ++ i) 
        p[i].y = std::lower_bound(b + 1, b + cnt + 1, p[i].y) - b;
    std::sort(p + 1, p + k + 1);
    for (int i = 1; i <= k; ++ i) {
        f[i] = Query(p[i].y) + p[i].num;
        ans = std::max(f[i], ans);
        Update(p[i].y, f[i]);
    }
    std::cout << ans << std::endl;
}

相關推薦

[OI][雜題]NO.1

NOIP 2015 跳石頭 題目背景 一年一度的“跳石頭”比賽又要開始了! 題目描述 這項比賽將在一條筆直的河道中進行,河道中分佈著一些巨大岩石。組委會已經選擇好了兩塊岩石作為比賽起點和終點。在起點和終點之間,有 N 塊岩石(不含起點和終 點的岩石)。在比賽過程中,選手們將從起點出發,每一步跳向相鄰的

雜題集萃[1]

register c++ n+1 pac sdi \n line 數據 name 題意 給出 $N$ 個形如 $f_i(x)=a_ix^2+b_i$ 的二次函數。 有 $Q$ 次詢問，每次給出一個 $x$，詢問 $max(f_i(x))$。 輸入格式 第一行兩個整數 $N$

python Leetcode刷題小記【No.1 兩數之和】

Leetcode 1 題目描述： 給定一個整數陣列和一個目標值，找出陣列中和為目標值的兩個數。 你可以假設每個輸入只對應一種答案，且同樣的元素不能被重複利用。 示例: 給定 nums = [2, 7, 11, 15], target = 9 因為 nums[0] + n

第九十題（1.不開辟暫時空間交換 2.刪除串中指定字符 3.推斷鏈表中存在環）

net 異或 img == pre def return 分享 存在 1.不開辟用於交換數據的暫時空間，怎樣完畢字符串的逆序 2.刪除串中指定的字符 3.推斷單鏈表中是否存在環 分析和代碼： 1，不開辟用於交換的暫時空間，能夠用異或交換。或者用字符串的‘\0‘位置的空

Web公路，新手上路！ No.1

under html html4 oos http org bsp web tran <!DOCTYPE> 　　用於告訴瀏覽器用何種HTML標準去讀取指令。 　HTML5: 　　<!DOCTYPE html> 　HTML4.01 strict:

【雜題集】【51NOD 1267】4個數和為0

www namespace quest color https question clas amp -a 4個數和為0 鏈接： 原題 題意： ... 這 思路： 由於（n=1000），O（n^2）的算法也可一試。

hdu 3641 數論 二分求符合條件的最小值數學雜題

main family pen gb2 code fine tracking math freopen http://acm.hdu.edu.cn/showproblem.php?pid=3641 學到： 1、二分求符合條件的最小值 /*====

一些DP雜題

algo type const else 範圍 one cnblogs 轉移 class 1. [HNOI2001] 產品加工 一道簡單的背包，然而我還是寫了很久QAQ 時間範圍是都小於5 顯然考慮一維背包，dp[i]表示目前A消耗了i的最小B消耗 註意 if(b[i

python基礎No.1

Coding 必須 用戶輸入 語言 組成 name 空格 連接 pri 版本python2 python語言不分"和‘，兩者可以一樣使用，同等效果 1.輸出print python3中print是一個函數 print "hello world" 輸出hello world

no.1

n) 操作 判斷 += getchar shel tdi 兩個 單引號 #include <stdio.h> #include <stdlib.h> void main() { int i; int sum = 0;

no.1 函數的重載

執行 情況 return 標準輸入 sha 個數 log cout 輸出流 //求3個數中最大的數，分別考慮整數，雙精度，長整數的情況 -1：主函數分3種情況，每種情況都是 +1：定義4個參數，3個是輸入變量，1個是輸出變量 +2：用標準輸入流輸入3個變量 +3：執行函數

BZOJ3629-聰明的燕姿【數學雜題】

cee left weibo sina iuc info ndt www. style T浪h改姆9少FVT優樂Phttp://www.docin.com/vwhd00606 AM0瓤XN7Ukahttp://weibo.com/u/6367436044 蹈4s釉畏耐E

編程題＃1：實現冒泡排序

using blog 超過 stream end clu pan cnblogs names 1 #include <iostream> 2 using namespace std; 3 4 int main() { 5 int n, a[

編程題＃1： 晶晶赴約會

color std () using main sin ret end iostream #include <iostream> using namespace std; int main() { int a; cin >> a;

NO.1 python安裝

pythonlinux安裝官網下載tar xzvf 解壓源碼安裝三大步./configuremakemake installvim python 自動補全http://www.jb51.net/article/58009.htmwindows安裝https://www.python.org/ftp/pytho

隨筆 | 這裏是一只大一的小菜雞 【NO.1】

java img 程序 win log tails nco 自己的 ide 今天裝了JDK以及IDEA準備進行學習 然後在裝JDK的過程遇到了小問題 在win10 1703中 網上的教程為 path添加%JAVA_HOME%\bin; 結果出現了cmd中輸入java

編程題＃1：單詞翻轉

-- end get cnblogs turn cin char line clu 描述 輸入一個句子（一行），將句子中的每一個單詞翻轉後輸出。 輸入 只有一行，為一個字符串，不超過500個字符。單詞之間以空格隔開。所謂單詞指的是所有不包含空格的連續的字符。 這道題請用

沖刺no.1

csu span 一個 用戶輸入 努力 spa 驗重 用戶添加 用戶信息 項目：ccsu小助手 角色：用戶 開發前：經過我們上一次我們對於自己成員的技術能力和性格分析，進行了相應的工作分配，讓每一個成員都能發揮出自己所擅長的東西，而我通過了隊友的認同，榮獲了客戶這一

git —— 基本命令以及操作（No.1）

src del 刪除 blog -1 comm commit 操作 提交 git基本命令（附加描述） 1.把文件添加到暫存區$ git add readme.txt 2.把暫存區的文件文件添加到倉庫$ git commit -m "提交說明" 備註：add添加單個文

NO.1 Docker的簡介

docker 容器化技術我今年19了，人生還有多少22K？ Docker是一個開源的應用容器化引擎,docker就像一個玻璃瓶子一樣,它使用的沙箱機制,相互之間不會有任何接口。Docker可以使開發者打包自己的應用和依賴包到一個容器中，並且這個容器是可移植的，然後發布到任何一臺生產環境的Linux機器上