[DP總結]狀壓DP
顧名思義,是用將狀態進行二進制壓縮成集合的形式來方便DP轉移的方法。
一些常用的代碼表示如下
i & j //取狀態i,j重合部分 i ^ j //取狀態i,j不同部分 i | j //合並狀態i,j (1 << N) - 1 //表示111…1(N個1) 1 << i - 1 //表示00100…0(1後面有i-1個0,也就是有且僅有二進制下第i位為1) for (int i = 0; i < n; ++ i) if (x & (1 << i)) cnt++; //統計當前狀態x的1的個數 while (x) if (x & 1) ans ++, x >>= 1; //上面的代碼也可以這麽寫
枚舉子集
既然是壓縮成集合的形式,那麽一個不可避免的問題就是如何枚舉子集。
假設我們有一個大小為n的集合,那麽統計子集數量的代碼如下。
for (int S = 1; S < (1 << n); ++ S)
for (int S0 = S; S0; S0 = (S0 - 1) & S)
//do some thing這個東西是NOIP2018提高初賽選擇第十題。
具體原理不管了。反正是二進制瞎搞。
簡單來說就是,如果要按普通方法枚舉子集,應該將S0從S開始每次減一,再判斷合法性。然而由於&S的結果只減不增,S0可以通過-1然後&S來直接到達最近合法狀態。
有必要分析一下這個代碼的時間復雜度。可以看出,對於一個元素個數為\(k\)的集合有\(C_n^k\)這麽多個,那麽時間復雜度為\(O(2^kC_n^k)\),又由二項式定理逆定理得\(2^kC_n^k=C_n^k1^{n-k}2^k=(2+1)^n\),故時間復雜度為\(O(3^n)\)。
[USACO08NOV]奶牛混合起來Mixed Up Cows
題目描述
Each of Farmer John‘s N (4 <= N <= 16) cows has a unique serial number S_i (1 <= S_i <= 25,000). The cows are so proud of it that each one now wears her number in a gangsta manner engraved in large letters on a gold plate hung around her ample bovine neck.
Gangsta cows are rebellious and line up to be milked in an order called ‘Mixed Up‘. A cow order is ‘Mixed Up‘ if the sequence of serial numbers formed by their milking line is such that the serial numbers of every pair of consecutive cows in line differs by more than K (1 <= K <= 3400). For example, if N = 6 and K = 1 then 1, 3, 5, 2, 6, 4 is a ‘Mixed Up‘ lineup but 1, 3, 6, 5, 2, 4 is not (since the consecutive numbers 5 and 6 differ by 1).
How many different ways can N cows be Mixed Up?
For your first 10 submissions, you will be provided with the results of running your program on a part of the actual test data.
POINTS: 200
約翰家有N頭奶牛,第i頭奶牛的編號是Si,每頭奶牛的編號都是唯一的。這些奶牛最近 在鬧脾氣,為表達不滿的情緒,她們在擠奶的時候一定要排成混亂的隊伍。在一只混亂的隊 伍中,相鄰奶牛的編號之差均超過K。比如當K = 1時,1, 3, 5, 2, 6, 4就是一支混亂的隊伍, 而1, 3, 6, 5, 2, 4不是,因為6和5只差1。請數一數,有多少種隊形是混亂的呢?
輸入輸出格式
輸入格式:
Line 1: Two space-separated integers: N and K
Lines 2..N+1: Line i+1 contains a single integer that is the serial number of cow i: S_i
輸出格式:
Line 1: A single integer that is the number of ways that N cows can be ‘Mixed Up‘. The answer is guaranteed to fit in a 64 bit integer.
輸入輸出樣例
輸入樣例#1:
4 1
3
4
2
1 輸出樣例#1:
2 說明
The 2 possible Mixed Up arrangements are:
3 1 4 2
2 4 1 3
狀壓DP的特點之一就是N特別小,一般最大不會超過23,通常在18附近。題目中的狀態通常可以抽象成一段或幾段連續的序列,每個元素有兩種選擇。對於這種狀態,通常可以使用狀態壓縮。眾所周知,2進制數可以看成是一個由0和1組成的序列。我們把2進制數的每一位對應原題目序列的每一個元素,0或1對應該元素選或不選。顯然共有\(2^N\)種可能性,當N在較小範圍內時,用一個數即可表示當前狀態。在本題中,我們先在最外層for(int i = 0; i <= ((1 << N) - 1); ++ i),表示枚舉所有可能的狀態,然後for(int j = 1; j <= N; ++ j) if (i & (1 << j - 1))表示當前枚舉到的狀態i的第j位為1,即選了第j位。這一層循環相當於\(O(N)\)枚舉了狀態i各位的所有是“1”的狀態,即選了的狀態。再for(int k = 1; k <= N; ++ k) if (!(i & (1 << k - 1)))與上面類似,這一層循環是對狀態的擴展(expand),看看是不是能從當前狀態的基礎上再多選一個,判斷可行的標準是否滿足狀態i,是否滿足題意,T < abs(a[k] - a[j])。如果滿足的話,那麽當前狀態\(dp[i][j]\),表示狀態為i時所選的最後一頭牛為j的方案數,就可以擴展成\(dp[i|(1<<k-1)][k]\),也就是為狀態為i再選上k,最後選的一頭牛為k的方案數貢獻一份自己的力量(霧)。既得狀態轉移方程為\(dp[i|(1 << k - 1)][k] += dp[i][j]\)。
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
#define fr(i, x, n) for(int i=(x);i<=(n);++i)
using namespace std;
typedef long long LL;
const int MAXN = 17;
int N, a[MAXN], K;
LL dp[1 << MAXN][MAXN];
template <typename _Tp>
inline void read(_Tp &x) {
char ch = getchar( ); _Tp f = 1; x = 0;
while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar( ); }
while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar( );
x *= f;
}
int Abs(int x) { return x < 0 ? -x : x; }
int main( ) {
read(N), read(K);
fr(i, 1, N) {
read(a[i]);
dp[1 << i - 1][i] = 1;
}
fr(i, 0, (1 << N) - 1) fr(j, 1, N)
if (i & (1 << j - 1)) fr(k, 1, N)
if (!(i & (1 << k - 1)) && Abs(a[k] - a[j]) > K)
dp[i | (1 << k - 1)][k] += dp[i][j];
LL ans = 0;
fr(i, 1, N) ans += dp[(1 << N) - 1][i];
printf("%lld\n", ans);
return 0;
} 總之……狀壓DP就是套路啊……
[05]:Cave Cows 1 洞穴裏的牛之一
總時間限制: 10000ms
單個測試點時間限制: 1000ms
內存限制: 262144kB
描述
很少人知道其實奶牛非常喜歡到洞穴裏面去探險。 洞窟裏有N(1≤N≤100)個洞室,由M(1≤M≤1000)條雙向通道連接著它們.每對洞室間至多只有一條雙向通道.有K(1≤K≤14)個洞室,裏面放有1捆幹草.牛吃1捆幹草,體重指數就會增加1. 貪吃的貝茜要到洞窟裏面探險.她希望能吃盡量多的幹草,但每條通道有一個寬度閾值,如果體重指數超過相應的閾值,貝茜就會被卡祝她從洞窟1出發,體重指數為0.在洞裏溜達一圈後,她要返回洞窟1. 那她最多能吃多少捆幹草呢?註意,貝茜經過一個洞室,不一定非要吃掉裏面的幹草.
輸入
第1行輸入N,M,K,之後K行每行一個整數,表示在這個洞室放有一捆幹草;接下來M行每行三個整數,表示一條雙向通道的起點終點和寬度閾值.
輸出
最多能吃掉的幹草數.
輸入輸出樣例
樣例輸入
6 7 5
1
2
3
4
5
1 2 3
3 6 2
6 2 10
2 4 1
5 1 1
4 5 1
1 6 1樣例輸出
4這題沒找到地方交……我也不知道代碼寫的對不對……
由於牛雖然在當前不會被卡,但是不知道下一個洞口是窄是寬,會不會被卡住……我們可以用Floyd預先處理出兩點之間所能達到的最大闕值。然後DP轉移就和上一題很像了,只是要特判一下1號洞穴有艹的情況,因為1號洞內的艹顯然可以留到最後吃而不用擔心被卡住的問題。
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
#define fr(i, x, n) for(int i=(x);i<=(n);++i)
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const int MAXM = 1010;
const int MAXN = 110;
const int MAXK = 15;
int N, M, K, m[MAXN][MAXN];
int dp[1 << MAXK][MAXN], ans, has[MAXN], flag;
template <typename _Tp>
inline void read(_Tp &x) {
char ch = getchar( ); _Tp f = 1; x = 0;
while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar( ); }
while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar( );
x *= f;
}
int Abs(int x) { return x < 0 ? -x : x; }
int main( ) {
read(N), read(M), read(K);
int a, b, c, x;
for (int i = 1; i <= K; ++ i) {
read(has[i]);
if (has[i] == 1) flag = 1;
}
memset(m, 63, sizeof(m));
for (int i = 1; i <= N; ++ i) m[i][i] = 0;
for (int i = 1; i <= M; ++ i) {
read(a), read(b), read(c);
//處理重邊
m[a][b] = min(m[a][b], c);
m[b][a] = m[a][b];
}
//用Floyd處理出兩點之間能達到的最大闕值
fr(k, 1, N) fr(i, 1, N) {
if (i == k) continue;
fr(j, 1, N) {
if (i == j || j == k) continue;
if (m[i][j] != INF)
m[i][j] = max(m[i][j], min(m[i][k], m[k][j]));
else m[i][j] = min(m[i][k], m[k][j]);
}
}
fr(i, 1, (1 << K) - 1) fr(j, 1, K)
if (i & (1 << j - 1)) {
fr(k, 1, K) if (!(i & (1 << k - 1))) {
if (m[has[j]][has[k]] < dp[i][j]) continue;
dp[i | (1 << k - 1)][k] = max(dp[i | (1 << k - 1)][k], dp[i][j] + 1);
}
//如果從該點能回到起點,更新答案
if (m[has[j]][1] >= dp[i][j]) ans = max(ans, dp[i][j]);
}
printf("%d\n", ans + flag);
return 0;
} [codevs] P1358 棋盤遊戲
時間限制: 1 s
空間限制: 64000 KB
題目等級 : 大師 Master
題目描述 Description
這個遊戲在一個有10*10個格子的棋盤上進行,初始時棋子位於左上角,終點為右下角,棋盤上每個格子內有一個0到9的數字,每次棋子可以往右方或下方的相鄰格子移動,求一條經過數字之和最小且經過0到9的所有數字的合法路徑,輸出其長度。(經過的數字包括左上角和右下角)
輸入輸出描述
輸入描述 Input Description
輸入包含10行,每行10個數字,以空格隔開,表示棋盤格子上的權值。數據保證存在合法路徑。
輸出描述 Output Description
輸出所求路徑的權值和。
樣例輸入輸出
樣例輸入 Sample Input
0 1 2 3 4 5 6 7 8 9
1 1 1 1 1 1 1 1 1 0
2 1 1 1 1 1 1 1 1 0
3 1 1 1 1 1 1 1 1 0
4 1 1 1 1 1 1 1 1 0
5 1 1 1 1 1 1 1 1 0
6 1 1 1 1 1 1 1 1 0
7 1 1 1 1 1 1 1 1 0
8 1 1 1 1 1 1 1 1 0
9 1 1 1 1 1 1 1 1 5樣例輸出 Sample Output
50數據範圍及提示 Data Size & Hint
【樣例解釋】
先一直向右走到第一行末尾,再豎直向下走位最優路徑。
比較簡單的狀壓DP。事實上BFS也可以過(我們假設它過不了)。矩形DP和狀壓DP的結合。思路很簡單,\(dp[i][j][k]\)表示前i行j列狀態為k的最小數字和。狀態轉移方程太好寫了= =\(dp[i][j][k]=Min(dp[i][j][k|(1<<m[i][j])], dp[i-1][j][k]+m[i][j], dp[i][j-1][k]+m[i][j])\)
/*
作者:曼珠沙華
題目:p1358 棋盤遊戲
*/
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MAXN = 12;
int m[MAXN][MAXN];
//dp[i][j][k]表示前i行j列狀態為k的最小數字和
int dp[MAXN][MAXN][1 << MAXN];
template <typename _Tp>
inline _Tp read(_Tp &x) {
char ch = getchar( ); bool f = 0; x = 0;
while (!isdigit(ch)) { if (ch == '-') f = 1; ch = getchar( ); }
while (isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar( ); }
if (f) x = -x; return x;
}
int main( ) {
memset(dp, 63, sizeof(dp));
for (int i = 1; i <= 10; ++ i)
for (int j = 1; j <= 10; ++ j) read(m[i][j]);
dp[1][1][1 << m[1][1]] = m[1][1];
for (int i = 1; i <= 10; ++ i)
for (int j = 1; j <= 10; ++ j)
for (int k = 0; k < (1 << 10); ++ k) {
if (i != 1) dp[i][j][k | (1 << m[i][j])] =
min(dp[i][j][k | (1 << m[i][j])], dp[i - 1][j][k] + m[i][j]);
if (j != 1) dp[i][j][k | (1 << m[i][j])] =
min(dp[i][j][k | (1 << m[i][j])], dp[i][j - 1][k] + m[i][j]);
}
printf("%d\n", dp[10][10][(1 << 10) - 1]);
return 0;
}P1441 砝碼稱重
題目描述
現有n個砝碼,重量分別為a1,a2,a3,……,an,在去掉m個砝碼後,問最多能稱量出多少不同的重量(不包括0)。
** 輸入輸出格式**
輸入格式:
輸入文件weight.in的第1行為有兩個整數n和m,用空格分隔
第2行有n個正整數a1,a2,a3,……,an,表示每個砝碼的重量。
輸出格式:
輸出文件weight.out僅包括1個整數,為最多能稱量出的重量。
輸入輸出樣例
輸入樣例#1:
3 1
1 2 2輸出樣例#1:
3** 說明**
【樣例說明】
在去掉一個重量為2的砝碼後,能稱量出1,2,3共3種重量。
【數據規模】
對於20%的數據,m=0;
對於50%的數據,m≤1;
對於50%的數據,n≤10;
對於100%的數據,n≤20,m≤4,m<n,ai≤100。
用狀壓的直觀思路就是枚舉每一種合法的去掉m個砝碼後的情況。假設現在有一個集合\(b[i]\)表示重量為i可以被稱出。那麽枚舉狀態的哪一位是1,如果是當前第j位是1,那麽之前稱過的所有重量都可以在原來的基礎上再加上\(w[j]\),也就是\(b<<w[j]\),那麽\(b=b|b<<w[j]\)。最後統計b中有多少個元素即可。這個b可以用bitset維護。
#include<bitset>
#include<cstdio>
#include<iostream>
#define f(i,x,n) for(int i=x;i<=n;++i)
using namespace std;
int n, m, a[21];
int ans;
int bit(int x) {
int cnt = 0;
f(i, 0, n - 1) if (x & (1 << i)) cnt++;
return cnt;
}
int main() {
cin >> n >> m;
f(i, 0, n - 1) cin >> a[i];
f(i, 0, (1<<n)-1) if (bit(i) == n - m) {
bitset<2010> t;
t[0] = 1;
f(j, 0, n - 1) if (i & (1<<j)) {
t = t | t << a[j];
ans = max(ans, (int)t.count());
}
}
cout << ans - 1 << endl;
return 0;
}P2622 關燈問題II
** 題目描述**
現有n盞燈,以及m個按鈕。每個按鈕可以同時控制這n盞燈——按下了第i個按鈕,對於所有的燈都有一個效果。按下i按鈕對於第j盞燈,是下面3中效果之一:如果a[i][j]為1,那麽當這盞燈開了的時候,把它關上,否則不管;如果為-1的話,如果這盞燈是關的,那麽把它打開,否則也不管;如果是0,無論這燈是否開,都不管。
現在這些燈都是開的,給出所有開關對所有燈的控制效果,求問最少要按幾下按鈕才能全部關掉。
輸入輸出格式
輸入格式:
前兩行兩個數,n m
接下來m行,每行n個數,a[i][j]表示第i個開關對第j個燈的效果。
輸出格式:
一個整數,表示最少按按鈕次數。如果沒有任何辦法使其全部關閉,輸出-1
** 輸入輸出樣例**
輸入樣例#1:
3
2
1 0 1
-1 1 0輸出樣例#1:
2說明
對於20%數據,輸出無解可以得分。
對於20%數據,n<=5
對於20%數據,m<=20
上面的數據點可能會重疊。
對於100%數據 n<=10,m<=100
我們當然是輸出無解啦其實這題比較簡單。根據題目定義,\(a[i]=0\)不管,那我們就不管了,當\(a[i]=1\)或\(a[i]=-1\)時,這是什麽操作?顯然是取反操作。\(f[i]\)表示狀態為i的最少按鈕數。轉移真的很簡單,看代碼。
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;
const int INF = 0x3f3f3f3f;
int n, m, a[110][1100];
int f[1100];
int main() {
cin >> n >> m;
for (int i = 1; i <= m; ++ i)
for (int j = 1; j <= n; ++ j)
cin >> a[i][j];
for (int i = 0; i < (1 << n); ++ i) f[i] = INF;
f[0] = 0;
for (int i = 0; i < (1 << n); ++ i)
for (int j = 1; j <= m; ++ j) {
int t = i;
for (int k = 0; k < n; ++ k)
if (((a[j][k + 1] == 1) && !(i & 1 << k)) ||
(a[j][k + 1] == -1) && (i & 1 << k))
t ^= 1 << k;
f[t] = min(f[t], f[i] + 1);
}
if (f[(1 << n) - 1] == INF) cout << "-1" << endl;
else cout << f[(1 << n) - 1] << endl;
return 0;
}
[HDU] P3001 Travelling
限制:6000/3000毫秒(Java /其他)內存限制:32768/32768 K
(Java /其他)總提交(7907):接受的提交(s):2590
問題描述
在coding了這麽多天之後,Acmer先生想要好好休息一下,旅行當然是最好的選擇!他已決定訪問N個城市,而Acmer先生堅持要訪問所有的N個城市!他也不介意哪個城市是他的起點,因為會有超人可以把他帶到任何城市,但只有一次召喚超人的機會。當然,這裏有m條道路會照常收費。不過Acmer先生太無聊了,他不想參觀同一城市兩次以上(不含兩次)!並且在此前提下,他想把總費用降到最低!他很懶惰,所以他找到了你,向你尋求幫助。
輸入
有多組測試數據,第一行是兩個整數n(1<n=10)和m,這意味著他需要訪問N個城市,可以選擇M條道路,然後接下來m行,每行三個整數a、b和c(1<a,b <=n),意思是a和b之間有一條路費用是C。
輸出
輸出他應該支付的最低費用,如果找不到這樣的路線,輸出-1。
有意思。簡化一下題意,就是給你一張無向圖(可能有重邊),你可以從任意一節點出發,在不經過同一城市兩次的前提下,經過所有的城市。某兩節點間有有權邊,問是否有解,如果有,最小費用是多少。可以看出本題事實上是TSP問題的變形,考慮每個節點最多只能經過兩次,也就是有0,1,2三種情況,所以要用鬼畜的三進制狀壓。我們先用一個\(p3[]\)數組表示3的多少次冪,\(p3[0] = 1\),直接遞推。正常的狀壓最重要的是狀態的壓縮,那麽如何將狀態壓縮成三進制呢?在二進制狀壓時,我們是用數在二進制表示下的每一位表示該對應元素的狀態,那麽我們顯然可以用一個數組模擬這個表達方式,設\(tri[i][j]\)表示狀態為\(i\)(\(i\)為三進制數)的第\(j\)位上的經過次數(不寫成try是因為和C++關鍵字沖突)。在更新時,根據題意,一共要滿足兩個條件:1.要經過所有城市(即\(tri[i][1…n]\)均不能為0);2.每個城市不能經過兩次(即\(tri[i][1…n]<=2\)),然後正常套路。
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MAXX = 60010;
const int MAXN = 12;
int n, w, m[MAXN][MAXN];
int p3[MAXN], tri[MAXX][MAXN], ans, dp[MAXX][MAXN];
//flag判斷當前狀態能否更新ans,flag2判斷是否有解
bool flag, flag2;
template <typename _Tp>
inline _Tp read(_Tp &x) {
char ch = getchar( ); bool f = 0; x = 0;
while (!isdigit(ch)) { if (ch == '-') f = 1; ch = getchar( ); }
while (isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar( ); }
if (f) x = -x; return x;
}
int main( ) {
p3[0] = 1;
for (int i = 1; i <= MAXN; ++ i) p3[i] = p3[i - 1] * 3;
//三進制數的轉化
for (int i = 1, tmp = i; i <= MAXX; ++ i, tmp = i)
for (int j = 1; j <= MAXX; ++ j) {
tri[i][j] = tmp % 3;
tmp /= 3;
if (!tmp) break;
}
while (scanf("%d%d", &n, &w) == 2) {
ans = INF; flag2 = false;
memset(m, 63, sizeof(m));
int x, y, z;
//處理重邊
for (int i = 1; i <= w; ++ i) {
read(x), read(y), read(z);
m[x][y] = min(m[x][y], z);
m[y][x] = m[x][y];
}
memset(dp, 63, sizeof(dp));
//任意一點均可作為起點且花費為0
for (int i = 1; i <= n; ++ i) dp[p3[i - 1]][i] = 0;
for (int i = 1; i < p3[n]; ++ i) {
flag = true;
for (int j = 1; j <= n; ++ j) {
//如果有某一位是0,說明有城市不能到達,不滿足條件,不更新答案
if (!tri[i][j]) flag = false;
for (int k = 1; k <= n; ++ k) if (k != j && tri[i][k] < 2)
dp[i + p3[k - 1]][k] = min(dp[i + p3[k - 1]][k], dp[i][j] + m[j][k]);
}
if (flag) for (int j = 1; j <= n; ++ j)
if (ans > dp[i][j]) ans = dp[i][j], flag2 = true;
}
if (!flag2) printf("-1\n");
else printf("%d\n", ans);
}
return 0;
}P1896 [SCOI2005]互不侵犯
題目描述
在N×N的棋盤裏面放K個國王,使他們互不攻擊,共有多少種擺放方案。國王能攻擊到它上下左右,以及左上左下右上右下八個方向上附近的各一個格子,共8個格子。
註:數據有加強(2018/4/25)
輸入輸出格式
輸入格式:
只有一行,包含兩個數N,K ( 1 <=N <=9, 0 <= K <= N * N)
輸出格式:
所得的方案數
** 輸入輸出樣例**
輸入樣例#1:
3 2輸出樣例#1:
16首先這道題並不是線性的了,而是矩形,卻又不是矩形DP。每個國王可以影響到一個3*3的範圍,這樣也比較難搞。考慮到每一行都是相似的,我們不妨將矩形分成若幹行來做。顯然對於每一行,我們可以\(O(2^nn)\)預處理出所有可行的狀態,每一行都必然是這些狀態中的其中一種。設\(dp[i][j][k]\)表示前i行,第i行狀態為j,放了k個國王的方案總數。然後對於每一行,枚舉可能狀態,枚舉放置的國王總數,再來一層枚舉上一行的狀態判斷合法(好暴力),因為當前行合法與否可以看成只與前一行狀態有關(感性理解),所以這樣顯然是對的。
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define f(i, x, n) for(int i=x;i<=n;++i)
using namespace std;
typedef long long LL;
const int MAXX = 110;
int N, K;
int tot, s0, s[MAXX], num[MAXX];
LL ans, dp[10][MAXX][MAXX];
int main() {
cin >> N >> K;
f(i, 0, (1 << N) - 1) {
if (i & (i << 1)) continue;
tot = 0;
f(j, 0, N - 1)
if (i & (1 << j)) tot++; //統計放置數量
s[++ s0] = i; //標記可行方案
num[s0] = tot;
}
dp[0][1][0] = 1;
f(i, 1, N) f(j, 1, s0) f(k, 0, K)
if (k >= num[j]) f(t, 1, s0)
if (!(s[t] & s[j]) && !(s[t] & (s[j] << 1)) && !(s[t] & s[j] >> 1))
dp[i][j][k] += dp[i - 1][t][k - num[j]];
f(i, 1, s0) ans += dp[N][i][K];
cout << ans << endl;
return 0;
}你要先大法師再打表我也不會攔你的。
#include<cstdio>
#include<iostream>
long long a[300]={
1,
4,0,0,0,
9,16,8,1,0,0,0,0,0,
16,78,140,79,0,0,0,0,0,0,0,0,0,0,0,0,
25,228,964,1987,1974,978,242,27,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
36,520,3920,16834,42368,62266,51504,21792,3600,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
49,1020,11860,85275,397014,1220298,2484382,3324193,2882737,1601292,569818,129657,18389,1520,64,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
64,1806,29708,317471,2326320,12033330,44601420,119138166,229095676,314949564,305560392,204883338,91802548,25952226,4142000,281571,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
81,2968,65240,962089,10087628,77784658,450193818,1979541332,6655170642,17143061738,33787564116,50734210126,57647295377,49138545860,31122500764,14518795348,4959383037,1237072414,224463798,29275410,2673322,163088,6150,125,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
},b,c;
int main(){
scanf("%d%d",&b,&c);
std::cout<<a[(b-1)*b*(2*b-1)/6+c-1];
}P2704 [NOI2001]炮兵陣地
題目描述
司令部的將軍們打算在NM的網格地圖上部署他們的炮兵部隊。一個NM的地圖由N行M列組成,地圖的每一格可能是山地(用“H” 表示),也可能是平原(用“P”表示),如下圖。在每一格平原地形上最多可以布置一支炮兵部隊(山地上不能夠部署炮兵部隊);一支炮兵部隊在地圖上的攻擊範圍如圖中黑色區域所示:
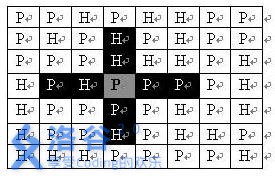
如果在地圖中的灰色所標識的平原上部署一支炮兵部隊,則圖中的黑色的網格表示它能夠攻擊到的區域:沿橫向左右各兩格,沿縱向上下各兩格。圖上其它白色網格均攻擊不到。從圖上可見炮兵的攻擊範圍不受地形的影響。 現在,將軍們規劃如何部署炮兵部隊,在防止誤傷的前提下(保證任何兩支炮兵部隊之間不能互相攻擊,即任何一支炮兵部隊都不在其他支炮兵部隊的攻擊範圍內),在整個地圖區域內最多能夠擺放多少我軍的炮兵部隊。
輸入輸出格式
輸入格式:
第一行包含兩個由空格分割開的正整數,分別表示N和M;
接下來的N行,每一行含有連續的M個字符(‘P’或者‘H’),中間沒有空格。按順序表示地圖中每一行的數據。N≤100;M≤10。
輸出格式:
僅一行,包含一個整數K,表示最多能擺放的炮兵部隊的數量。
輸入輸出樣例
輸入樣例#1:
5 4
PHPP
PPHH
PPPP
PHPP
PHHP輸出樣例#1:
6這個影響範圍比互不侵犯更鬼畜。十字???不會下一個
這樣每一行不僅要受到前一行的影響,還要受到前一行的前一行的影響,這咋辦?
這題範圍不大,我們不妨鬼畜暴力一點,他不是受兩行影響嗎?我把他轉化成只受前一行影響就行了。如何轉化?反正都狀壓了,也沒人說不能一次壓兩行啊?
設\(dp[i][j][k]\)表示當前狀態是i,上一行狀態是j,當前考慮到了第k行。
先處理出第一行,然後依次遞推,各種神奇玄學的判斷,然後你會發現
這題就沒了MLE了。
讓dp的最後一維滾將dp的最後一維滾動優化成[3]。然後就真沒了。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define f(i, x, n) for(int i=x;i<n;++i)
using namespace std;
const int MAXN = 100;
const int MAXM = 10;
int N, M, ans;
int t[MAXN], sum[(1<<10)], dp[(1<<10)][(1<<10)][3];
void init() {
cin >> N >> M;
f(i, 0, N) f(j, 0, M) {
char x; cin >> x;
t[i] <<= 1, t[i] += (x == 'H' ? 1 : 0);
}
}
int getsum(int i) {
int tot = 0;
while(i) { if (i & 1) ++ tot; i >>= 1; }
return tot;
}
bool pd(int s) { return ((s & (s << 1)) || (s & (s << 2))); }
int main() {
init();
f(i, 0, (1 << M)) sum[i] = getsum(i);
f(l, 0, (1 << M)) f(s, 0, (1 << M))
if (!(l & s || l & t[0] || s & t[1] || pd(l) || pd(s)))
dp[l][s][1] = sum[s] + sum[l];
f(i, 2, N) f(l, 0, (1 << M)) {
if (l & t[i - 1] || pd(l)) continue;
f(s, 0, (1 << M)) {
if (s & t[i] || l & s || pd(s)) continue;
f(p, 0, (1 << M)) {
if (p & l || p & s || p & t[i - 2] || pd(p)) continue;
dp[l][s][i % 3] = max(dp[l][s][i % 3],
dp[p][l][(i - 1) % 3] + sum[s]);
}
}
}
f(l, 0, (1 << M)) f(s, 0, (1 << M))
ans = max(ans, dp[l][s][(N - 1) % 3]);
cout << ans << endl;
return 0;
}[DP總結]狀壓DP
