樹形DP和狀壓DP和揹包DP

阿新 • • 發佈：2018-11-05

樹形DP和狀壓DP和揹包DP

樹形\(DP\)和狀壓\(DP\)雖然在\(NOIp\)中考的不多,但是仍然是一個比較常用的演算法，因此學好這兩個\(DP\)也是很重要的。而揹包\(DP\)雖然以前考的次數挺多的，但是現在基本上已經成了人人都能AK的題了，所以也不經常考了。

樹形DP

樹形DP這個非常特殊，他好像和是唯一一個用深搜實現的DP，所以我們學好它也是應該的，其特點是通過深搜。

思路

先找到一個根節點，然後預處理出所有子樹的大小。
然後深搜把最底層的子節點得狀態處理出來。
遞歸回溯到根節點，在回溯的時候完成狀態轉移。最後輸出根節點的值。

\(Example\)

\(LuoguP2014\)（選課）這個題，就是一個比較典型的樹形DP，順便還考察了一下分組揹包，

首先我們分析一下狀態我們可以設\(dp[i][j]\)表示以\(i\)的子樹中選\(j\)個（包括\(i\)自己）所得到的最大學分，因此我們可以採用樹形\(DP\)的方法。

首先預處理出\(dp[i][1]\)表示只選\(i\)自己所得到的學分，然後我們可以進行狀態轉移，因為題目給的輸入滿足\(0\)一定是唯一的根節點，所以最後我們只要輸出\(dp[0][m]\)首先我們要得到狀態轉移方程，然後仔細，細心的考慮邊界條件，這也是一般DP的思路，首先我們可以得出方程：

\(dp[i][j] = max（dp[i][t] + dp[son(i)][j - t]）（j\in[1, ~m],t\in [1,j]]且son(i)要全列舉一遍）\)

,此時我們還要處理比較棘手的問題，就是轉移的順序，

首先這是一個01揹包所以我們要\(for(j = m; j >= 1; j--)\)而t的範圍也是一個坑點，因為在推到t時，我們首先要滿足比t小的一定要枚舉出來，所以我們就要\(for(t = 1; t <= j; t++)\)

這個題基本上就解決了,程式碼：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector>
using namespace std;
vector <int> son[100010];
int s[100010], out_degree[100010], in_degree[100010];
int dp[1000][1000];//表示i的子樹選j個課程 
int n, m;
inline void dfs(int a)
{
    for (int i = 0; i < son[a].size(); i++)
    {                                   
        int to = son[a][i];             
        dfs(to);
        for (int j = m + 1; j >= 1; j--) //總共選m個加上0，就是m + 1個 
            for (int t = j; t >= 1; t--)
        dp[a][j] = max(dp[a][j], dp[a][j - t] + dp[to][t]);  
    }
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        son[a].push_back(i); 
        dp[i][1] = b;
        dp[i][0] = 0;
    }   
    dfs(0);
    printf("%d", dp[0][m + 1]);
}
/*
7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2
*/

狀壓DP

狀壓\(DP\)就更神奇了，可以說是最有\(OI\)特點的一個\(DP\)，因為它用到了位運算和二進位制。因此像那些一個區間只有選或不選的操作的那些狀態可以用二進位制表示，然後在用一些不同尋常的東西，例如左移右移使可以狀態轉移。而判斷是否是狀壓DP時可以檢視資料範圍，如果在\(20\)以內就可以使用狀壓\(DP\)。

思路

跟其他的\(DP\)一樣，我們首先還是要尋找狀態，但是這個狀態可能比較難搞，所以我們就需要壓縮一下，也可以刪除一些沒有用的東西，且需要滿足這些狀態都很相似，且數量很多，此時就可以把它當成狀態了。(總的來說，是先壓縮狀態，然後尋找合理狀態)
在壓縮的時候需要運用位運算的一些操作
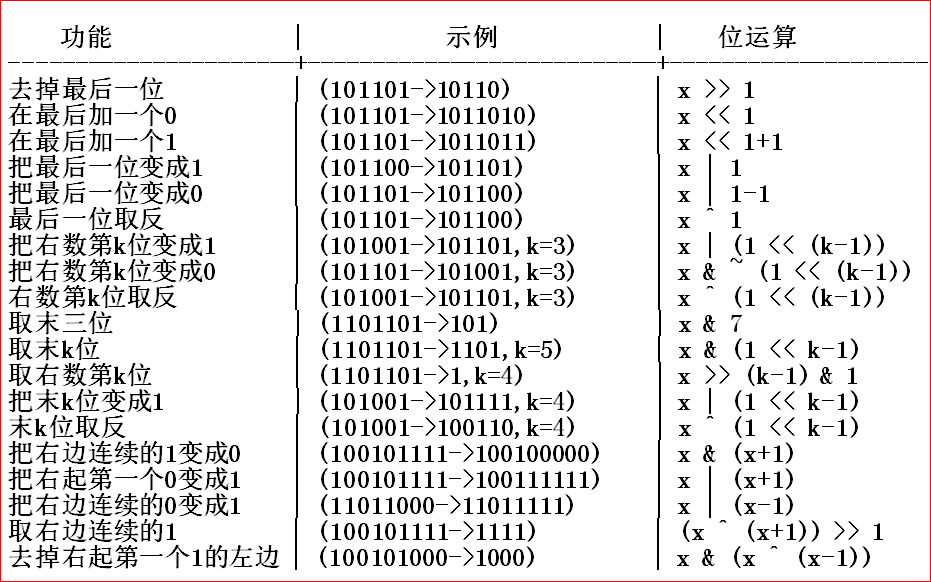
當然一些運算的順序也要記清楚，防止除錯時間太長還找不到什麼錯誤，

位反（~ ) > 算術 > 位左移、位右移 > 關係運算 > 與 > 或 > 異或 > 邏輯運算

\(Example\)

\(LuoguP1879\)也是一個經典題，也經常被拿來用作寫狀壓DP的入門題，當然憤怒的小鳥也是一個只要寫過幾個狀壓DP的就都能寫出來的演算法，因此也可以做一做，

我們分析一下玉米田這道題，題目讓我們求總共有多少種方案數，而且資料範圍還很小，這就在暗示我們採用狀壓\(DP\)的方法和套路。

預處理

首先應該壓縮狀態，且基本上狀壓\(DP\)壓縮都是一樣的方法

壓縮狀態+預處理程式碼：

for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++)
        scanf("%d", &flag[i][j]);//判斷土地是否肥沃
for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++)
        now[i] = (now[i] << 1) + flag[i][j];//壓縮狀態，狀壓DP的一般思路

尋找合理狀態

題目要求要滿足三個條件，即左右不能相鄰，上下不能相鄰，土地不能荒蕪，為了方便，我們先使其滿足左右不能相鄰。

滿足這個條件的前提是

(!(\(i\) & (\(i\) <<1))) && (!(\(i\) & (\(i\)>>1)))

就是該狀態左移和右移一位並與該狀態\(and\)的結果是零，即並沒有左移一位後的某一位與左移一位前的某一位相同，因為如果相同的話，就說明左右相鄰

尋找合理狀態程式碼：

for (int i = 0; i < (1 << m); i++）
    if ( (!(i & (i << 1))) && (!(i & (i >> 1))) ) 
        check[i] = 1;//說明此狀態可行

狀態轉移

以上都是一行的預處理，現在我們要跨過這個界限，開始多行的轉移了，在進行多行的轉移的時候，就需要判斷第二個條件，就是上下之間不能有相鄰的狀態。

滿足這個條件的前提是

! (\(last\) & \(now\))

還需要判斷第三個條件，不能有土地是荒蕪的，這個也很好判斷，因為我們已經預處理出每一行的最難的滿足條件\(now[i]\), 如果(一個狀態 & \(now[i]\)) == 該狀態，說明此狀態一定滿足不荒蕪，到此所有的條件都已經分析完畢，如果不懂可以手糊。

那就可以狀態轉移了，狀壓就成為了普通的二維DP了。

狀態轉移程式碼：

for (int i = 1; i <= n; i++)
    for (int j = 0; j < (1 << m); j++)
        if (check[j] && (now[i] & j) == j)//判斷此狀態可不可行，且不能有荒蕪的土地， 
            for (int k = 0; k < (1 << m); k++)
                if (!(k & j) && check[k])//上下不能有相鄰的地方，比如如果上：10010，下：01100，那他們and的結果就不為0 
                        dp[i][j] = (dp[i][j] + dp[i - 1][k]) % mod;

樹形DP和狀壓DP和揹包DP