資料結構作業12—樹和森林(選擇題)
2-1下列線索二叉樹中(用虛線表示線索),符合後序線索樹定義的是: (2分)
- A
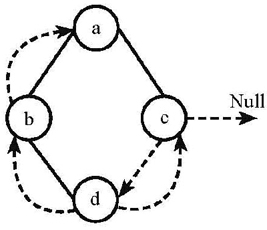
- B

- C
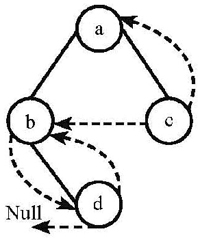
- D
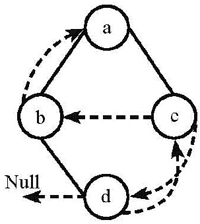
作者: DS課程組
單位: 浙江大學
2-2將森林轉換為對應的二叉樹,若在二叉樹中,結點u是結點v的父結點的父結點,則在原來的森林中,u和v可能具有的關係是: (3分)
1.父子關係; 2. 兄弟關係; 3. u的父結點與v的父結點是兄弟關係
- A.1、2和3
- B.1和3
- C.1和2
- D.只有2
作者: DS課程組
單位: 浙江大學
2-3具有65個結點的完全二叉樹其深度為(根的深度為1): (3分)
- A.5
- B.6
- C.7
- D.8
作者: DS課程組
單位: 浙江大學
2-4已知一棵完全二叉樹的第6層(設根為第1層)有8個葉結點,則該完全二叉樹的結點個數最多是: (3分)
- A.119
- B.52
- C.111
- D.39
注:即第六層有32個節點,其中有8個是葉子節點,說明其餘24個是有子節點的,又由於是完全二叉樹,所以那24個節點每個節點有2個子節點,共計48個節點,也就是第七層的節點有48個,所以前六層的63加第七層的48就是111個節點了
作者: DS課程組
單位: 浙江大學
2-5具有1102個結點的完全二叉樹一定有__個葉子結點。(3分)
- A.1063
- B.551
- C.不確定
- D.79
注:設n2為度為2的節點,n1為度為1的節點,n0為度為0的節點;
邊數n=節點數-1,即n=1101;
n=2n2+n1;
完全二叉樹度為1的節點只能有0個或1個(不信可以畫畫看一下)
所以n1=0或者1用n=2n2+n1;算一下,n2肯定是整數,把0捨去;
求出n2=550;
度為0的節點數等於度為2的節點數+1;
所以葉子節點數為551
作者: 何欽銘
單位: 浙江大學
2-6由若干個二叉樹組成的森林F中,葉結點總個數為N,度為2的結點總個數為M,則該集合中二叉樹的個數為: (3分)
- A.N−M−1
- B.無法確定
- C.N−M
- D.M−N
作者: DS課程組
單位: 浙江大學
2-7若森林F有15條邊、25個結點,則F包含樹的個數是:(2分)
- A.11
- B.10
- C.9
- D.8
注:分析:森林中樹的個數與結點數的關係推導。
先看一般性的解決策略:根據一棵樹的邊數+1=結點數。
可以知道,每多一棵樹,結點數就少一個。
即,
一棵樹時,邊數 = 結點數-1
兩棵樹時,邊數 = 結點數-2
….
n棵樹時,邊數 = 結點數-n
於是得到:25-15 = 10.
有時候,可能過於關注區域性特徵,沒能體會到巨集觀的特性。但是可用特值迅速解決:15條邊全是一棵樹的,那麼這棵樹有16個結點,剩下9個結點都不再形成邊,即一個結點算一棵樹。那麼,共1+9 = 10棵樹。
原文解析:https://blog.csdn.net/u011240016/article/details/53260683
作者: DS課程組
單位: 浙江大學
2-8設森林F中有三棵樹,第一、第二、第三棵樹的結點個數分別為M1,M2 和M3 。則與森林F對應的二叉樹根結點的右子樹上的結點個數是: (2分)
- A.M3
- B.M2 +M3
- C.M1 +M2
- D.M1
注:第一棵樹構成根和左子樹,因此右子樹上的結點個數就是M2 + M3
作者: DS課程組
單位: 浙江大學
2-9在一個用陣列表示的完全二叉樹中,如果根結點下標為1,那麼下標為17和19這兩個結點的最近公共祖先結點在哪裡(陣列下標)? (注:兩個結點的“公共祖先結點”是指同時都是這兩個結點祖先的結點) (3分)
- A.2
- B.1
- C.4
- D.8
作者: DS課程組
單位: 浙江大學
2-10對於一個有N個結點、K條邊的森林,共有幾棵樹? (2分)
- A.N−K−1
- B.不能確定
- C.N−K+1
- D.N−K
注:邊數 = 結點數-樹數
作者: DS課程組
單位: 浙江大學
