作者：Vernon
說明：本文主要以列表形式將B+樹的特點以及注意點等列出來，主要參考《演算法導論》、維基百科、各大部落格的內容，結合自己的理解寫的，如內容有不當之處，請各位雅正。
出處：http://blog.csdn.net/love_u_u12138
轉載請註明出處。

1.前言

B樹是為磁碟或其他直接存取的輔助儲存裝置而設計的一種平衡搜尋樹。B樹類似於紅黑樹，但它們在降低磁碟I/O運算元方面要更好一些。現在許多資料庫系統使用B樹或者B樹的變種(B+樹和B*樹)來儲存資訊。B樹用的比較普遍，許多書籍、部落格都有詳細的介紹，對於B樹的嚴格定義也相對統一，在這裡就不予贅述。
B+樹是B樹的一種變形，它把所有的衛星資料都儲存在葉節點中，內部節點只存放關鍵字和孩子指標

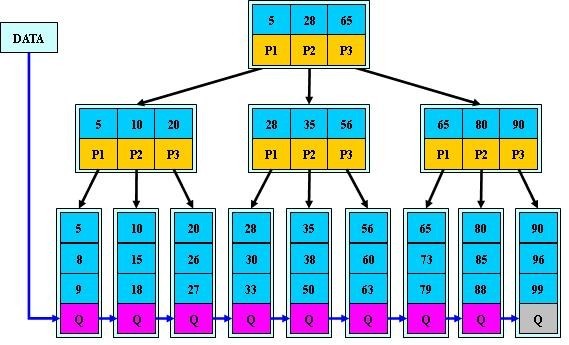
以下先放一張我所依據的B+樹的圖示(這張圖有所簡化，下面講完定義後會貼一張更加詳細的圖，兩圖本質並無差異)：

2.定義

B+樹的定義我沒有找到官方的定義(如果有找到的人望告知我)，有些定義在論壇還有爭議，但是這些並沒有多大影響，只是一點小小的差異，下面的定義中有涉及爭議的部分我會提及。

B+樹的定義如下：

1. 每個節點node有下面的屬性：
   
   • n個關鍵字key[1],key[2], … ,key[n]，以非降序存放，使得key[1]≤key[2]≤…≤key[n]；
   • isRoot，一個布林值，如果node是根節點，則為TRUE；否則為FALSE；
   • isLeaf，一個布林值，如果node是葉子節點，則為TRUE；否則為FALSE；
   • Node*型別的parent指標，指向該節點的父節點
2. 每個內部節點還包含n個指向其孩子children[0],children[1], … , children[n]，葉子節點沒有孩子。（注：此處有爭議，B+樹到底是與B 樹n-1個關鍵字有n棵子樹保持一致，還是B+樹n個關鍵字的結點中含有n棵子樹；兩種定義都可以，只要自己實現的時候統一用一種就行。如無特殊說明，以下的都是後者：即n個關鍵字對應n棵子樹）；
3. 內部節點的關鍵字對儲存在各子樹中的關鍵字範圍加以分割：如果key[i]為任意一個儲存在內部節點中的關鍵字，childNum[i]為該節點的對應下標的子樹指標指向的節點的任意一個關鍵字，那麼
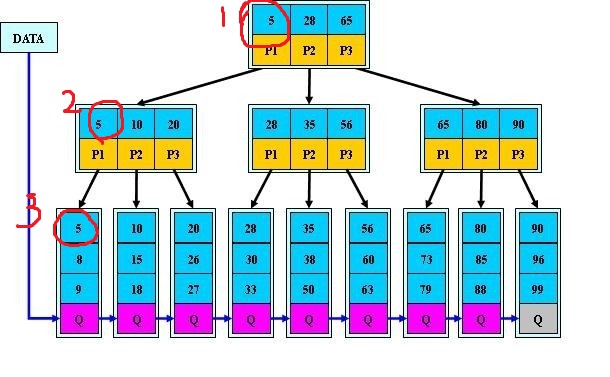
   key[1] ≤ childNum[1] < key[2] ≤ childNum[2] < key[3] ≤ childNum[3] < … < key[n] ≤ childNum[n]

4. 內部節點並不儲存真正的資訊，而是儲存其葉子節點的最小值作為索引。比如下圖，標註1和標註2都是內部節點，裡面儲存的並不是真正的資訊，而是標註3所示的節點中的最小值。(注：此處有爭議以最大值作為索引，同樣也是不影響的爭議)
   

5. 任何和關鍵字相聯絡的“衛星資料(satellite information)” 將與關鍵字一樣存放在葉子節點中，一般地，可能只是為每個關鍵字對應的”衛星資料”存放一個指標，指標指向存放實際資料的磁碟頁，匹配了某個葉子節點的關鍵字即可通過該指標找到其他對應資料。

6. 每個葉子節點還有指向下一個節點的指標next，方便遍歷整棵B+樹。
7. 每個葉子節點具有相同的深度，即樹的高度h。
8. 每個節點所包含的關鍵字個數有上界和下界，用一個被B+樹的最小度數(minmum degree)的固定整數t≥2來表示這些界：
   
   • 除了根節點以外的每個節點必須至少有t個關鍵字。因此，除了根節點以外的每個內部節點至少有t個孩子
   • 每個節點至多有2t個關鍵字，因此，一個內部節點至多可有2t個孩子。當一個節點恰好有2t個關鍵字時，稱該節點是滿的。

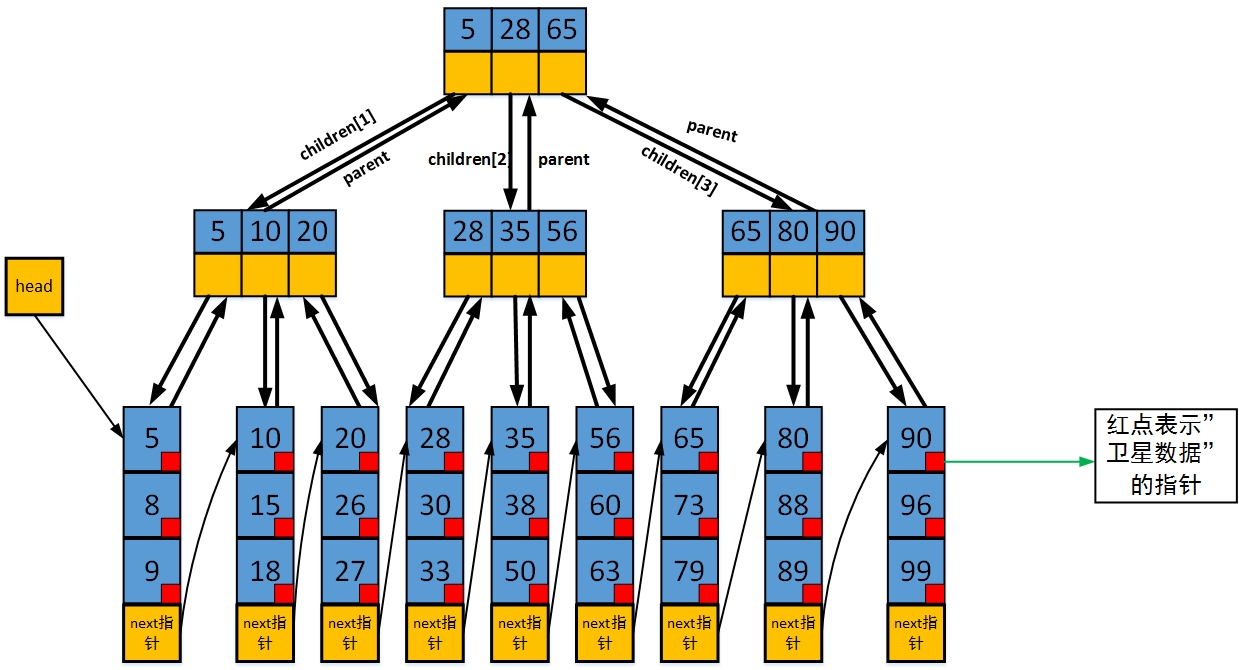
結合以上的具體定義，下面這張圖更加詳細的描述了一棵具體的B+樹

3.注意點

在B+樹的學習與實現過程中，也遇到不少的疑惑之處，現記錄如下，持續更新：

• 內部節點並不儲存真正的資訊，而是儲存其葉子節點的最小值作為索引。每次插入刪除都進行更新(此時用到parent指標)，保持最新狀態。
• 關於所有葉子節點都處於同一深度是如何實現的？這與B+樹具體的插入和刪除演算法有關。簡單解釋一下插入時的情況，根據插入值的大小，逐步向下直到對應的葉子節點。如果葉子節點關鍵字個數小於2t，則直接插入值或者更新衛星資料；如果插入之前葉子節點已經滿了，則分裂該葉子節點成兩半，並把中間值提上到父節點的關鍵字中，如果這導致父節點滿了的話，則把該父節點分裂，如此遞歸向上。所以樹高是一層層的增加的，葉子節點永遠都在同一深度。下面是我實現的B+樹中的插入程式碼的片段：

/** 插入關鍵字key */
    public void insert(Comparable key, Object obj, BPlusTree tree)
    {
        // 葉子節點則插入
        if (isLeaf) {
            // 不需要分裂直接插入
            if (containsKeyword(key) || keywords.size() < tree.getDegree()) {
                insertInNotFull(key, obj); // 直接插入
                if (parent != null) {
                    parent.updateAfterInsert(tree); // 更新父節點的資訊(將最小的值存到父節點的關鍵字中作為索引)
                }
                // 需要分裂成左右兩個節點
            } else {
                splitNode(key, obj, tree);
            }
            // 如果不是葉子節點則繼續往下搜尋
        } else {
            Node leafNode = downToLeaf(key);        // 逐步向下到對應的葉子節點
            leafNode.insert(key, obj, tree);
        }
    }

4.結語

B+樹還有一個最大的好處，方便掃庫，B樹必須用中序遍歷的方法按序掃庫，而B+樹直接從葉子結點挨個掃一遍就完了，B+樹支援range-query非常方便，而B樹不支援。這是資料庫選用B+樹的最主要原因。 –樑斌