一、你對回溯演算法的理解

1、回溯演算法就是一種有組織的系統最優化搜尋技術，可以看作蠻力法窮舉搜尋的改進。回溯法常常可以避免搜尋所有可能的解，所以它適用於求解組織數量較大的問題。

2、首先我們先了解一下一個基本概念“解空間樹”：問題的解空間一般使用解空間樹的方式來組織，樹的根節點位於第1層，表示搜尋的初始狀態，依次向下排列。

3、解空間樹的動態搜尋：在搜尋至樹中任一節點時，先判斷該節點對應的部分是否是滿足約束條件，或者是否超出目標函式的界，也就是判斷該節點是否包含問題的最優解。如果肯定不包含，則跳過對該節點為根的子樹的搜尋，即所謂的剪枝；否則，進入該節點為根的子樹，繼續按照深度優先策略搜尋。（這也是為什麼回溯可以避免搜尋所有的解）

4、在搜尋過程中，通常採用兩種策略避免無效搜尋：

      （1）用約束條件剪除得不到的可行解的子樹

　  （2）用目標函式剪取得不到的最優解的子樹

　　  （這兩種方式統稱為：剪枝函式）

5.在用回溯法求解問題時，常常遇到兩種典型的解空間樹：

　（1）子集樹：但所有的問題是從n個元素的集合中找出滿足某種性質的子集時，相應的解空間樹成為子集樹

　（2）排列樹：當所給出問題是確定n個元素滿足某種性質的排列時，相應的解空間稱為排列樹。          

6.回溯法的一般步驟：

　　（1）設定初始化的方案（給變數賦初始值，讀入已知資料等）

　　（2）變換方式去試探，若全部試完側轉（7）

　　（3）判斷此法是否成功（通過約束函式），不成功則轉（2）

　　（4）試探成功則前進一步再試探

　　（5）正確方案還是未找到則轉（2）

　　（6）以找到一種方案則記錄並列印

　　（7）退回一步（回溯），若未退到頭則轉（2）

　　（8）已退到頭則結束或列印無解

7.回溯法的優點在於其結構明確，可讀性強，易於理解，而且通過對問題的分析可以大大提高執行效率。

二、請說明“子集和”問題的解空間結構和約束函式

1、解空間結構

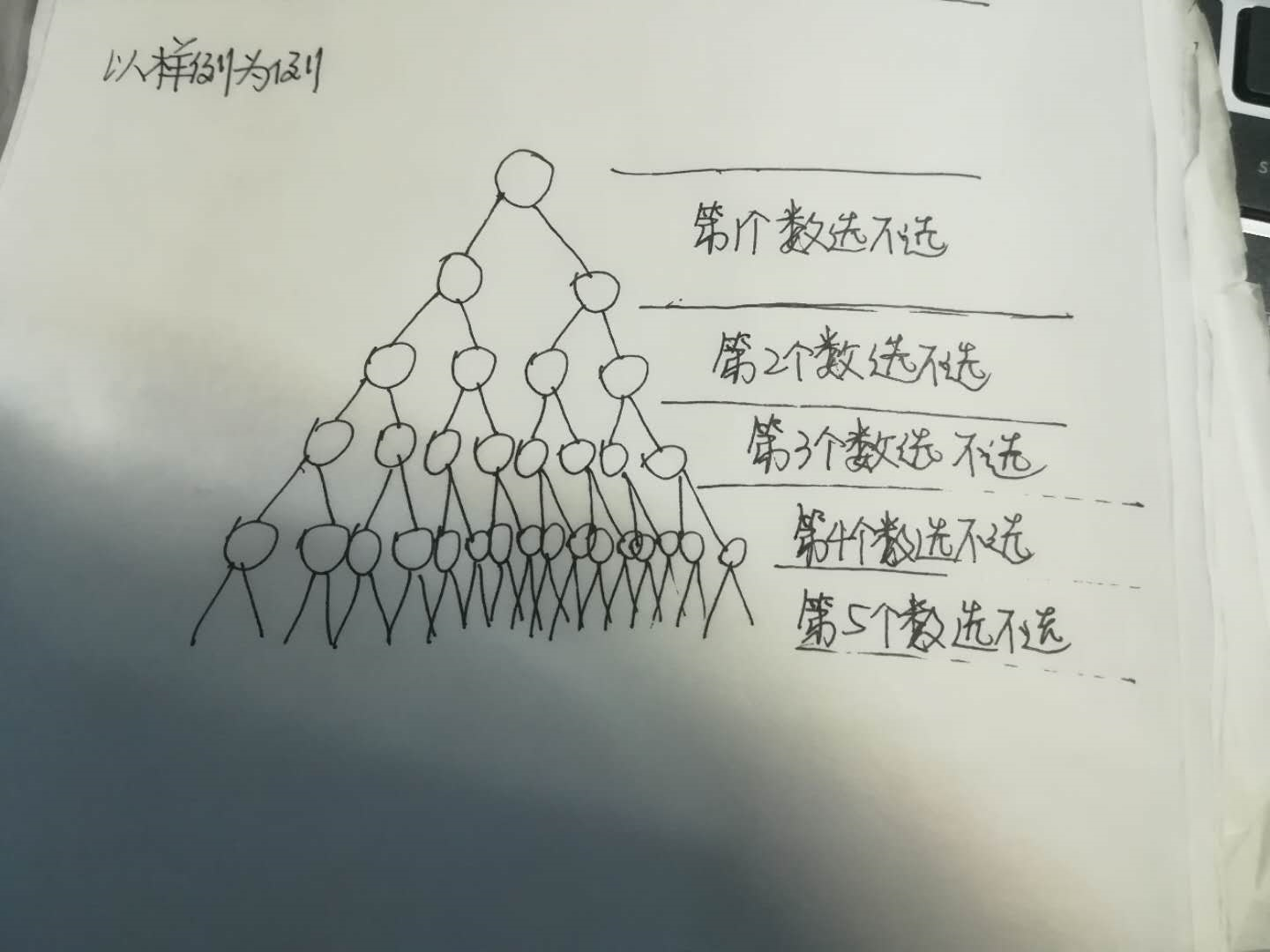
2、約束函式

（1）當前的子集和大於題目要求的子集和時，捨棄當前節點，不再往下搜尋

（2）用一個rest變數記錄當前元素到最後一個元素的和，如果當前的和加上rest的和大於要求的子集和，則進入右子樹

程式碼實現：

#include<iostream>
using namespace std;
int n;//集合大小
int c;//要求的和 
int rest = 0;//從當前元素加到最後一個元素的總和，用來限界減枝 
int S[10000];//元素陣列 
int cc=0;//當前的子集和
int choose[10000];//設定第i個數是否選 
bool backtrack(int i) 
{
    if(cc == c )
        return true;
    if(i > n)
        return false;
    rest -= S[i]; 
    if(cc+S[i] <= c)//可以取S[i]，在子集樹中表示走左分支 
    {
        choose[i]=1;
        cc+=S[i];
        if(backtrack(i+1))
            return true;
        cc-=S[i];//回溯時要把之前加的減掉 
    }
    if(cc+rest>=c)//沒辦法確實不行，利用rest判斷限界減枝，在子集樹中表示走右分支 
    {
        choose[i] = 0;
        if(backtrack(i+1))
            return true; 
    }
    rest += S[i];
    return false;
}

int main()
{
    cin>>n>>c;
    for(int i=1;i<=n;i++)
    {
        cin>>S[i];
        rest += S[i];
    }
    if(!backtrack(1))cout<<"No Solution!";
    else 
    {
        for(int i=1;i<=n;i++)
        {
            if(choose[i])//若為1則表示選擇了
                cout<<S[i]<<" "; 
        }
    }
    return 0;
}

3、請說明在本章學習過程中遇到的問題及結對程式設計的情況

我覺得回溯法還是比較難的，遇到的最大問題就是畫出瞭解空間樹但是卻不知道如何確定限界函式，對於回溯的過程也不是很理解，需要每道題都細摳除錯才能比較清楚它的過程。跟隊友結對程式設計一個學期以來，現在比較有默契了，她總是能很快發現我程式碼的問題，這樣比一個人敲程式碼要有效率。