深度學習中的梯度下降優化演算法綜述
1 簡介
梯度下降演算法是最常用的神經網路優化演算法。常見的深度學習庫也都包含了多種演算法進行梯度下降的優化。但是,一般情況下,大家都是把梯度下降系列演算法當作是一個用於進行優化的黑盒子,不瞭解它們的優勢和劣勢。
本文旨在幫助讀者構建各種優化演算法的直觀理解,以幫助你在訓練神經網路的過程中更好的使用它們。本文第二部分先簡單敘述了常見的梯度下降優化演算法;第三部分敘述了神經網路訓練過程中存在的挑戰;第四部分,我們將討論一系列常見的優化演算法,研究它們解決這些挑戰的動機及如何推匯出更新準則;第五部分,我們將探討如何在並行和分散式環境下如何優化梯度下降的演算法和結構;第六部分,我們將探討其他有助於優化梯度下降法的策略。
梯度下降法,目的是最小化目標函式 , 表示一個模型的引數,核心思想是沿著目標函式相對於引數的梯度 的反方向持續移動以更新引數。學習率 表示每次更新時的移動步長。總之,梯度下降可以想象成在由目標函式形成的“山峰”(超平面)上,沿著各點處下降最快的方向持續前進,直到我們遇到由超平面構成的“谷底”。
2 梯度下降變體
常見的有三種梯度下降的變體演算法,相互之間的區別是每次使用多少樣本計算目標函式相對於引數的梯度。根據每次更新時使用的樣本數量,我們其實是在引數更新的準確性和每次引數更新的耗時之間進行權衡。
2.1 批梯度下降演算法
批梯度下降,每次基於全部的訓練樣本集計算損失函式相對於引數的梯度。公式為:
每次更新時都需要使用全部的訓練樣本計算梯度,好處是梯度計算準確,劣勢是梯度計算量大,更新速度慢。特別是對於太大的無法全部載入到記憶體中的資料集,無法使用批梯度下降法進行更新。批梯度下降法也無法進行引數的線上更新,這是因為不能在執行中加入新的樣本進行計算。
批梯度下降法的虛擬碼為:
for i in range(nb_epochs):
param_grad = evaluate_gradient(loss_function,data,param)
params = params - learning_rate * param_grad
對於預先定義的epoch數量,我們首先計算整個訓練樣本集的損失函式相對於引數param的梯度向量param_grad。注意,在最新的深度學習庫中,提供了自動求導功能,可以高效、快速地求得函式對於特定引數的梯度。如果自己實現求梯度的程式碼,則需要進行“梯度檢查”(注:CS231n中給出了關於梯度檢查的指導)。
計算出梯度之後,沿著梯度的反方向,以學習率乘梯度為步長,進行梯度的更新。
批梯度下降法可以保證凸函式收斂到全域性最小值,或者是非凸函式收斂到區域性極小值。當然在深度學習中,損失函式一般是一個非凸函式,目前學者們猜想,對於足夠大的神經網路而言,大部分區域性極小值都具有很小的代價函式,我們能不能找到真正的全域性最小點並不重要,而是需要在引數空間中找到一個代價很小(但不是最小)的點,因此收斂到一個區域性最小值也是一個可以接受的結果。(摘抄自 《深度學習》)
2.2 隨機梯度下降演算法
隨機梯度下降(SGD)和批梯度下降演算法相反,每次只使用單個樣本進行進行引數更新。使用單個樣本對
,首先計算出損失函式值,然後按照下式進行引數更新:
因此批梯度下降法在每次更新引數前,會對相似的樣本計算梯度,因此在較大資料集上計算會有些冗餘。而SGD每次更新僅對單個樣本求梯度,去除了這些冗餘,因而更新速度較快並可進行線上學習。
SGD的缺點是每次更新值的方差很大,在頻繁更新下,目標函式值存在著劇烈的波動,如下圖所示。
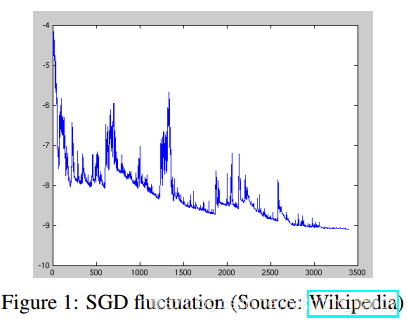 圖 1
圖 1
通俗解釋下上圖,假如當前選中的樣本在當前引數下預測label和真實label很接近,損失函式值很小,那麼本次的引數更新就不需要大幅度的變動;但是,假如當前選中的樣本在更新後的引數下預測label和真實label差距很大,損失函式值很大,那麼就需要進行大幅度的引數更新。表現出來就是損失函式值無法持續的穩定下降,而是存在大範圍的波動。
相比於批梯度下降有可能會收斂到一個區域性極小值,SGD收斂過程中的波動,有可能會幫助目標函式跳到一個可能更小的區域性極小值。但是,SGD也會使得收斂的過程變得複雜,因為該方法可能持續的波動而不會停止。實驗結果也表明,當慢慢減小學習率時,SGD可以取得和批梯度下降同樣的收斂效果,使得非凸函式收斂到區域性極小值、凸函式收斂到全域性最小值。
下面的虛擬碼也表明了SGD是在批梯度下降的基礎上加了一個對每個樣本的遍歷,計算每個樣本的損失函式,然後使用損失函式相對於引數的梯度進行更新。不過要注意的是在開始每個epoch的更新之前,先對樣本集進行了shuffle操作。
for i in range(nb_epochs):
np.random.shuffle(data)
for example in data:
param_grad = evaluate_gradient(loss_function,example,param)
params = params - learning_rate * param_grad
2.3 Mini-Batch梯度下降
mini-batch梯度下降每次使用大小為n的小批次訓練樣本進行引數更新。更新公式為:
好處是:
- 減少了引數更新中的方差,可以取得較穩定的收斂效果;
- 可以使用目前常用的深度學習庫中高度優化的矩陣乘法操作提升梯度計算的效率。
常用的mini-batch大小為50-256,但是也可以根據具體的應用進行調整。
小批量梯度下降演算法,通常是我們訓練神經網路的首選演算法。現在,我們一般就用SGD來表示小批量梯度下降演算法。下文對於隨機梯度下降演算法的介紹中,為方便起見,就省略了子式中的引數x(i:i+n),y(i:i+n)。
小批量梯度下降演算法的虛擬碼為:
for i in range(nb_epochs):
np.random.shuffle(data)
for batch in get_batchs(data,batch_size = 50):
param_grad = evaluate_gradient(loss_function,batch,param)
params = params - learning_rate * param_grad
2.4 小結
目前經常使用小批量梯度下降演算法,而不是批量梯度下降演算法的原因是:n個樣本均值的標準差是 ,其中 是樣本值真實的標準差。分母 表明使用更多樣本來估計梯度的方法的回報是低於線性的。比較兩個假象的梯度計算,一個基於100個樣本,另一個基於10000個樣本,後者需要的計算量是前者的100倍,但卻只降低了10倍的均值標準差。如果能夠快速地計算出梯度估計值,而不是緩慢地計算準確值,那麼大多數優化演算法會收斂地更快。
小批量的大小通常由以下幾個因素決定:
- 更大的批量會計算更精確的梯度估計,但是回報卻是小於線性的;
- 極小批量通常難以充分利用多核架構。這促使我們使用一些絕對最小批量,低於這個值的小批量處理不會減少計算時間;
- 如果批量處理中的所有樣本可以並行地處理(通常確是如此),那麼記憶體消耗和批量大小會正比。對於很多硬體設施,這是批量大小的限制因素;
- 在某些硬體上使用特定大小的陣列時,執行時間會更少。尤其是在使用 GPU 時,通常使用 2 的冪數作為批量大小可以獲得更少的執行時間。一般, 2 的冪數的取值範圍是 32 到 256, 16 有時在嘗試大模型時使用;
- 可能是由於小批量在學習過程中加入了噪聲,它們會有一些正則化效果 。 泛化誤差通常在批量大小為 1 時最好。因為梯度估計的高方差,小批量訓練需要較小的學習率以保持穩定性。因為降低的學習率和消耗更多步驟來遍歷整個訓練集都會產生更多的步驟,所以會導致總的執行時間非常大。
3 挑戰
小批量梯度下降演算法,也無法保證良好的收斂效果,同時也帶來了一系列需要解決的問題:
- 選擇適當的學習率是一個難題。太小的學習率會導致較慢的收斂速度,而太大的學習率則會阻礙收斂,並會引起損失函式在最小值處震盪,甚至有可能導致結果發散;
- 我們可以設定一個關於學習率的列表,如通過退火的方法,在學習過程中調整學習率 —— 按照一個預先定義的列表、或是當相鄰迭代epoch中損失函式的變化小於一定閾值時來降低學習率。但這些列表或閾值,需要根據資料集的特性,提前定義;
- 此外,我們對所有的引數都採用了相同的學習率。但如果我們的資料比較稀疏,同時特徵有著不同的出現頻率,那麼我們不希望以相同的學習率來更新這些變數,我們希望對較少出現的特徵有更大的學習率;
- 在對神經網路最優化非凸的罰函式時,另一個通常面臨的挑戰,是如何避免目標函式被困在無數的區域性最小值中,以導致的未完全優化的情況。Dauphin 認為,這個困難並不來自於區域性最小值,而是來自於“鞍點”,也就是在一個方向上斜率是正的、在一個方向上斜率是負的點。這些鞍點通常由一些函式值相同的面環繞,它們在各個方向的梯度值都為0,所以SGD很難從這些鞍點中逃離。
4 梯度下降優化演算法
下面介紹目前深度學習中常用的解決上述挑戰的優化演算法。這裡沒有介紹不適合於高維資料集的優化演算法,例如牛頓法等二階優化演算法。
4.1 動量
SGD很難在具有陡峭邊的峽谷 —— 一種在一個方向的彎曲程度遠大於其他方向的彎曲程度的區域中實現良好的優化,但是這種情況在區域性極小值處很常見。在峽谷中,如下圖黑線所示,SGD在峽谷的窄軸上震盪,向區域性極值處緩慢地前進。
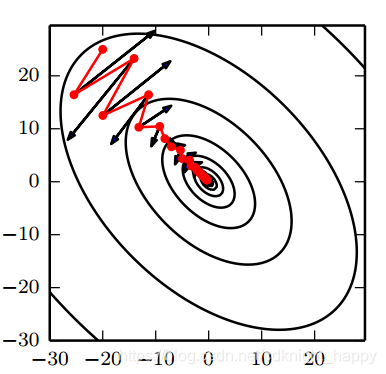 圖 2
圖 2
動量法,如圖2中紅線所示,會幫助SGD在正確優化方向上加速前進,並減小震盪。實現上是通過在原有項前新增一個引數
,迭代公式如下所示:
動量引數
一般會設定為0.9或其他差不多的值。
動量演算法累積了之前梯度指數級衰減的移動平均,並且繼續沿著該方向移動。在擬合一組含有噪聲但是有明顯分佈點的分佈趨勢時,可以用到指數加權平均這一方法,即每在第n次計算當前值時,都將前n-1的值通過加權的方式求和,使計算當前值能夠儲存前面的資料分佈趨勢,而又由於加權衰減,越早的資料影響越小,比直接用平均值的方式更優。
假如
=0.9,則
。
由於對於小數 ,有 ,同時由於 實際上是由一個指數衰減函式和資料點做內積的結果,而當這個指數衰減減小到
