Andrew Ng’s Coursera Machine Leaning(ML) Notes Week2

Author: Yu-Shih Chen
December 22, 2018 6:55 PM

Intro：
本人目前是在加州上大學的大二生，對人工智慧和資料科學有濃厚的興趣所以在上學校的課的同時也喜歡上一些網課。主要目的是希望能夠通過在這個平臺上分享自己的筆記來達到自己更好的學習/複習效果所以notes可能會有點亂，有些我認為我自己不需要再複習的內容我也不會重複。當然，如果你也在上這門網課，然後剛好看到了我的notes，又剛好覺得我的notes可能對你有點用，那我也會很開心哈哈！有任何問題或建議OR單純的想交流OR單純想做朋友的話可以加我的微信：y802088

Week3

大綱：

1. Classification
2. Hypothesis Representation
3. Decision Boundary
4. Cost Function
5. Simplified Cost Function and Gradient Descent
6. Advanced Optimization
7. Multiclass Classification: One-vs-all
8. The Problem of Overfitting
9. Cost Function
10. Regularized Linear Regression
11. Regularized Logistic Regression

Classification

Classification跟之前學的不一樣的地方就在我們要predict的東西不是一個數值（如：yes or no）， 但我們只要把它轉換為數值（0和1）就可以了。我們先學習binary classification problem，也就是隻會有0和1的output。

Section 重點：這個section主要就是introduce classification的大概思路。

Hypothesis Representation

在學習如何表達我們的預測公式之前，有一個核心的公式需要知道，那就是：Sigmoid Function（also known as Logistic function)。
Sigmoid Function表示式：

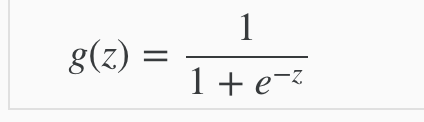
為什麼需要知道這個呢？之前也說了，做classification類的問題的時候我們需要將我們的result的值放到0和1，而這個公式的圖示畫出來的話：

這個sigmoid function的output絕對不會超過1，也就是可以將我們之前學過的Linear Regression裡面的公式套入裡面：

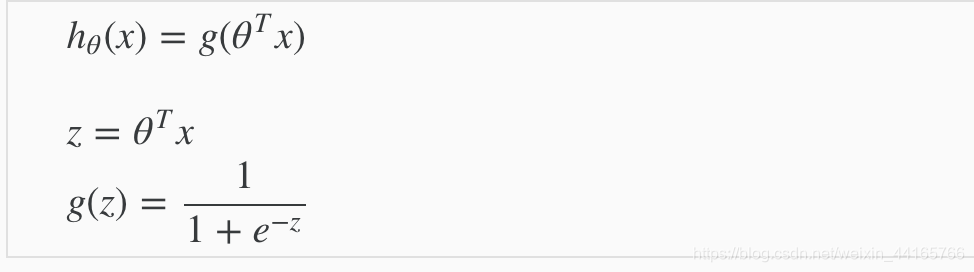
這樣我們得出的結果，就會是得到“1”的概率。 （比如說如果我們套入這個預測公式後得到0.7，那就代表我們得到的預測就是“1”的機率有70%，“0”的機率有30%。）而我們要做的，就是給公式設定一個threshold（如：if h_x > 0.5 = 1)來決定它predict 1還是0.

Section 重點：將linear regression的預測公式plug到sigmoid function裡面就可以得到“1”的概率。

Decision Boundary

我們需要決定一個threshold來預測我們最終的值。上一個section講了我們的預測公式可以預測出得到“1”的概率，這個section講的如何用threshold來更好地理解我們的logistic regression model是怎麼predict value的
我們再來看一次sigmoid的function：

如圖所示，x軸表示的就是我們的’z’ 也就是linear regression用的h_x（預測公式Theta’ * X) 那z>0 的時候就會超過50%也就會predict 1，我們就可以通過 這個資訊有個更好的瞭解logistic regression是怎麼運作的。 而且decision boundary出來了之後，是跟我們的training set沒有關聯的。所以theta學習完畢後，decision boundary不會根據data set而改變（就相當於我們week 2畫出來的線）。
以下是一個example：

如果theta訓練出這3個值，那我們就知道如果我們的x1 小於或等於5的話，就會預測出1。
section 重點：通過sigmoid function和我們定的threshold來更好地瞭解我們的logistic regression的運作。得出的decision boundary是我們train完了之後的h_x的一個property，跟training set是沒有關係的。

Cost Function

week 2的時候忘記講，但是linear regression model是永遠都只有一個global minima的，所以我們不用擔心gradient descent會跑到local minimum去。但是如果我們套用一樣的公式給logistic regression，那將會製造很多的local minimum也就有可能不會達到最低點。
所以我們有另外一套公式：

用圖表表示出來的話：

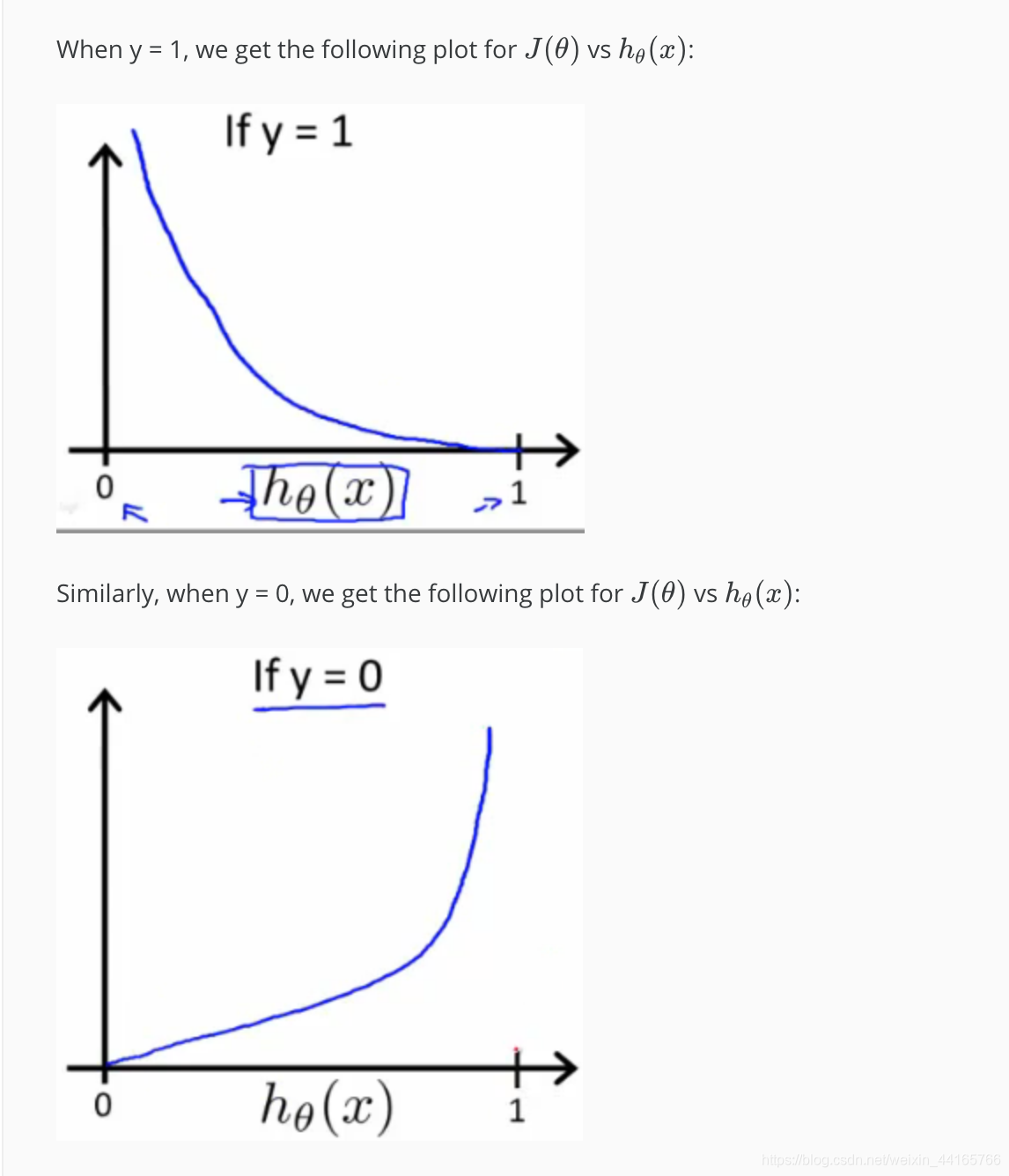
通過這樣的公式就會讓它只有一個global minima。後面會有將他們combine成一個公式的寫法，這個section主要目的是為了解釋我們新的cost function的思路。

section重點：如果直接套用linear regression 的cost function, 那將不止一個local minima。所以我們需要一套新的公式來表達我們的cost function for logistic regression.

Simplified Cost Function and Gradient Descent

上個section講到的cost function這個section會把它簡化到一個公式裡，就不用分開implement了更方便！
公式為：

為什麼能這樣寫呢？因為大佬們很聰明。如果y = 1的話，那後半部分的equation就為0，只剩下前半段。而前半段是不是剛好就是y = 0的時候的cost function? (詳細參考上個section）。相反y=0的時候也一樣，前半段會為0只剩下後半段。這樣我們就不需要特地分開2部分來寫我們的程式碼了。
這個section還講了gradient descent的公式。
公式為：

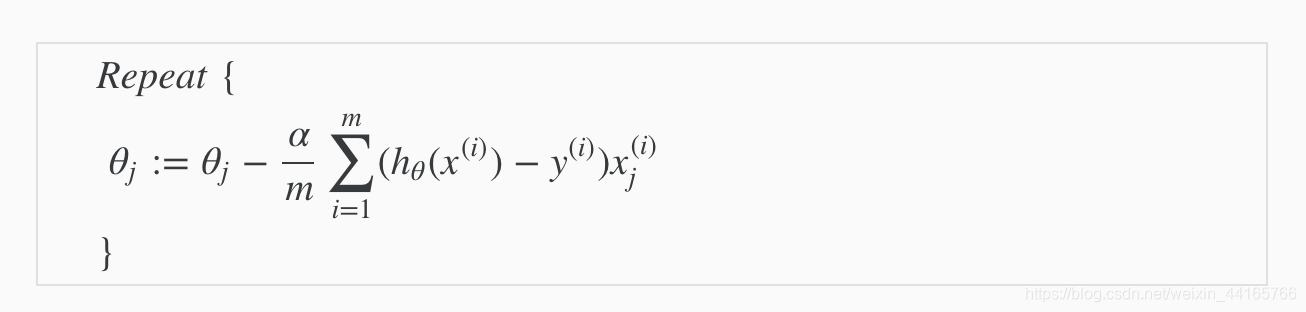
是不是跟linear regression的gradient descent一模一樣？不一樣！要注意這裡的h(x)是代入sigmoid function之後得出的預測。

section重點：cost function可以寫成一條公式了。gradient descent乍一看跟linear regression的一模一樣，但是要小心這裡的h_x是帶入sigmoid 後的預測，跟linear regression的時候是不一樣的！

Advanced Optimization Algorithms

這個section非常重要也有用。 它主要講了除了gradient descent以外的一些找theta的演算法：

1. Gradient Descent
2. Conjugate Gradient
3. BFGS
4. L-BFGS

這些演算法跟gradient descent比的好處是：

• 不用自己選擇alpha（learning rate) 演算法會自動幫你選擇最好的alpha
• 更快，更有效率
• 更復雜，比較難debug

Implement的準備條件：

1. 計算J(theta)，也就是我們的cost function
2. 計算根據每一個theta的gradient（也就是partial derivative）做成一個跟theta一樣大的矩陣。
3. 可以寫一個function計算這兩樣東西：
   function [jVal, gradient] = costFunction(theta)
   jVal = […code to compute J(theta)…];
   gradient = […code to compute derivative of J(theta)…];
   end
   這裡寫的程式碼也就是做一個可以return jVal（我們的cost）和gradient（partial derivative）的function。作業裡要求寫的就是這個function。

Implementation：

options = optimset(‘GradObj’, ‘on’, ‘MaxIter’, 100);
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

利用我們上面寫的function，這個演算法在MATLAB和OCTAVE上的寫法如上。
註釋：

• ‘GradObj’ 和‘on’就是說我們會提供gradient。
• ‘MatIter’ 和 ‘100’ 就是我們設定的迴圈多少次（演算法自帶loop）
• initialTheta就是我們設定theta的初始值，這裡全部為0
• optTheta, functionVal, exitFlag分別為演算法得出的結論，這裡的optTheta就是我們想要的theta值，而exitFlag會return 一個integer來表示它認為converge了沒。具體用’help fminunc’程式碼來了解。

至於這些演算法具體是怎麼運作的is well beyond the scope of this class。 但是Andrew說就是他也是在用了好一段時間了之後才真的瞭解他們的執行構造的。所以就算不知道他們具體是怎麼執行的也完全可以拿來使用。要注意一點就是必須n>=2, 也就是必須得有2個或以上的theta值這個演算法才能跑。

Section 重點：除了gradient descent外還有其他的advanced optimization algorithms。他們比gd要更有效率而且更省事情。後面的作業基本上都是用advanced opt algorithms來找theta，很少再implement gradient descent了。記得n>=2，也就是theta的數量要至少有2個。

Multiclass Classification One-vs-All

這個section講了如何將我們上面討論的binary class運用到multiclass裡面，也就是說我們的y不只有0和1，而是可以有01234567…n。
看圖 ：


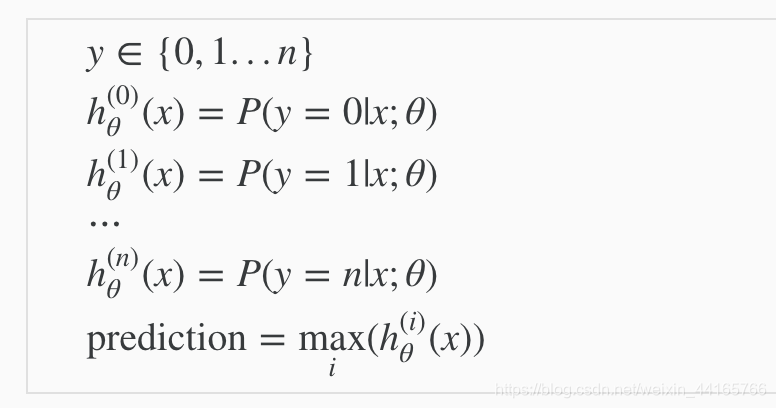
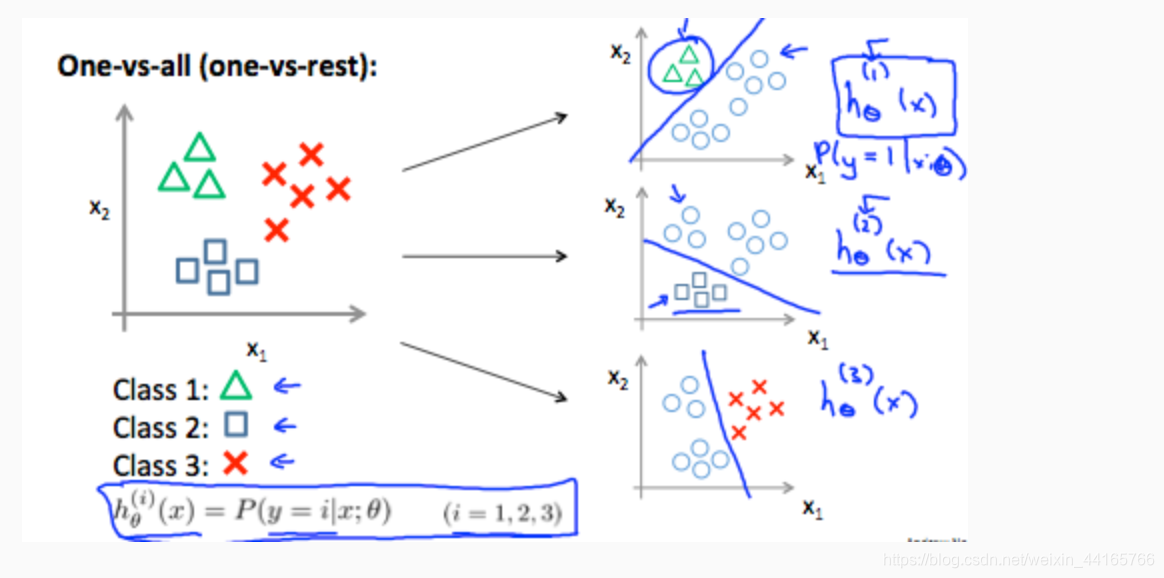
如圖所示，現在的h_x預測出來的值就會代表得到i（也就是y）的機率。他會分成很多個binary class來預測。 這裡有3個class，所以分成3次，每次都跟你剩下的class一起對比。我們會得到3個值，分別為3個class的機率，而寫個max的程式碼找出哪一個機率最高就行了。簡單地說就是分成i個binary class生成i個結果，從中挑選最好的。

Section 重點：從binary class（2個output 0和1）到multiclass的應用。

Week 3就到這裡啦！（作業寫在另一個文章裡）
Thanks for reading!