Andrew Ng's Coursera Machine Leaning Coding Hw 1
Andrew Ng’s Coursera Machine Leaning Coding Hw 1
Author: Yu-Shih Chen
December 21, 2018 4:17AM
Intro:
本人目前是在加州上大學的大二生,對人工智慧和資料科學有濃厚的興趣所以在上學校的課的同時也喜歡上一些網課。主要目的是希望能夠通過在這個平臺上分享自己的筆記來達到自己更好的學習/複習效果所以notes可能會有點亂,有些我認為我自己不需要再複習的內容我也不會重複。當然,如果你也在上這門網課,然後剛好看到了我的notes,又剛好覺得我的notes可能對你有點用,那我也會很開心哈哈!有任何問題或建議OR單純的想交流/單純想做朋友的話可以加我的微信:y802088
Week 2 Coding Assignment
大綱:
- Warm-up Exercise
- Plot Data
- Cost Function
- Gradient Descent
Warm-up Exercise
function A = warmUpExercise() %WARMUPEXERCISE Example function in octave % A = WARMUPEXERCISE() is an example function that returns the 5x5 identity matrix A = []; % ============= YOUR CODE HERE ============== % Instructions: Return the 5x5 identity matrix % In octave, we return values by defining which variables % represent the return values (at the top of the file) % and then set them accordingly. A = eye(5,5) % =========================================== end
這個沒什麼好講的,就是做一個5x5的identity matrix,一行就完事了。
Plot Data
function plotData(x, y) %PLOTDATA Plots the data points x and y into a new figure % PLOTDATA(x,y) plots the data points and gives the figure axes labels of % population and profit. figure; % open a new figure window % ====================== YOUR CODE HERE ====================== % Instructions: Plot the training data into a figure using the % "figure" and "plot" commands. Set the axes labels using % the "xlabel" and "ylabel" commands. Assume the % population and revenue data have been passed in % as the x and y arguments of this function. % % Hint: You can use the 'rx' option with plot to have the markers % appear as red crosses. Furthermore, you can make the % markers larger by using plot(..., 'rx', 'MarkerSize', 10); data = load('ex1data1.txt'); X = data(:,1); y = data(:,2); m = size(X,1); % number of training sets plot(X,y,'rx','MarkerSize',10); ylabel('Profit in %10,000s'); xlabel('Population of City in 10,000s'); % ============================================================ end
這裡就是extract我們需要的資料也就是X(features)和y(results)。Specifically,我們要通過一個城市的population(X)去預測profit for food truck(y)。 這個section只是把提供的資料庫給用xy圖表畫出來而已:

Compute Cost
這個section要寫出我們的J(cost function)也就是誤差公式:
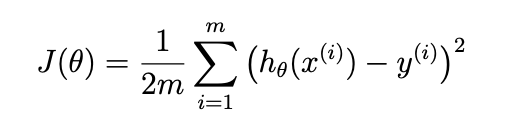
function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
% J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
% parameter for linear regression to fit the data points in X and y
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
% You should set J to the cost.
h_x = X * theta;
J = sum((h_x - y).^2) / (2*m)
% =========================================================================
end
這裡注意好矩陣之間的關係就好。這裡X加了1列的 ‘1’(預設值,詳細看coursera的視訊教程)之後是 m x 2 (m = sample的總量),而theta被我們初始為theta = zeros(2, 1); 也就是2 x 1的matrix(全部為0)。所以h_x (預測值)就是X * theta,出來的是個m x 1 的vector,也就跟我們的y一樣(請參考linear algebra的矩陣乘法)。 之後再把h_x帶到我們的公式裡就好,簡單粗暴。
Gradient Descent
這裡有2種寫法,個人認為第二種比較全面所以比較好,但第一次做的時候可能第一種會比較容易理解。
第一種:
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
h_x = X * theta; % m x 1 vector
%Do not need to loop over theta since only 2
temp1 = theta(1) - (alpha * sum(h_x - y) / m);
temp2 = theta(2) - (alpha * sum((h_x - y).* X(:,2))/m);
% Store in temp because we don't want to change theta value before using it.
theta(1) = temp1;
theta(2) = temp2;
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end
end
這裡有幾個需要注意的點:
- 需要將theta存進temp裡面,因為如果直接assign的話它執行theta2的時候就會使用一個跟theta1不一樣的theta(因為被更改theta1的時候改掉了)。
- 如果theta的元素更多,那將會需要用for loop來給所有的theta做gradient descent(也就是第二種寫法)
第二種:
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
h_x = X * theta; % m x 1 vector
temp = theta;
% For loop to loop over elements in temp
for i = 1:size(theta,1)
temp(i) = theta(i) - (alpha * sum((h_x - y).* X(:,i))/m);
% Store in temp because we don't want to change theta value before using it.
theta = temp;
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end
end
這裡是將theta存進一個temp的矩陣(還是一樣的原因,避免更改theta的值)然後用一個for loop計算所有在‘temp’裡面的元素的gradient descent,最後將計算好的temp來更改theta。這是一次的gradient descent的迴圈,將這個環節進行多次便能找到理想的theta值。
用contour graph和xy-graph來visualize我們的結果:

我們可以看到這個紅色的‘x’也就是我們的誤差值已經到達了3d圖接近谷底的地方,也就是接近最低值的地方。

我們可以拿來跟最開始的graph作比較,可以發現這是一個還算不錯的line of fit。做到這裡就可以恭喜你做出了你的第一個用machine learning算出的預測公式啦!(此處應有掌聲啪啪啪)
Week2 的coding作業(required section)就到這裡啦。
Thanks for reading!
