前言

Paxos演算法是用來解決分散式系統中，如何就某個值達成一致的演算法。它晦澀難懂的程度完全可以跟它的重要程度相匹敵。目前關於paxos演算法的介紹已經非常多，但卻很少有人能對P2c提出自己的見解，大多數是和稀泥式的人云亦云。但我相信真理是越辯越明的，只有旗幟鮮明的亮出自己的觀點，供大家討論，才能學到東西。

我個人認為理解Paxos有兩個關鍵：

1. 為什麼要對提案進行順序編號（或者說更大的編號意味著什麼）。
2. 為什麼Promise能保證一致性（答案隱含在第1點中）

一致性問題

假設有一組伺服器儲存了使用者的餘額，初始是100塊，現在使用者提交了兩個訂單，一個訂單是消費10元，一個訂單是充值

一致性演算法並不保證所有提出的值都是正確的（這可能是安全管理員的職責）。我們假設所有提交的值都是正確的，演算法需要對到底該選哪個做出決策，並使決策的結果被所有參與者獲悉。

在正式開始介紹Paxos所面臨的難題前，為了表述方便，先提一下Paxos演算法中的三個角色，後面會比較頻繁的用到：

• Proposer：議案發起者。
• Acceptor：決策者，可以批准議案。
• Learner：最終決策的學習者。

我們虛擬一個一致性問題的場景：有一個使用者小綠，現在要對他的姓氏資訊進行修改，此時有多個不同的議案被提出，如何就最終的結果達成一致。

首先看一下下面這種最簡單的情況：A1接受了Pa的議案“趙”，A2和A3接受了Pb的議案“錢”，那麼最終小綠應該姓什麼？

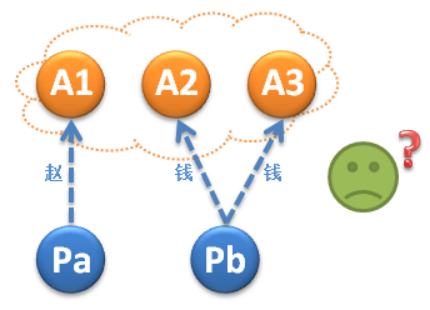
答案很簡單：超過半數的的議案就是最終的選定值。小綠應該姓“錢”！在議案提交後，Pa和Pb只要查詢一下小綠姓氏，很容易就能查到 “錢”的數量超過半數，因此Pb的議案將會返回“成功”，Pa的議案將會返回“失敗”。

P0. 當叢集中，超過半數的Acceptor接受了一個議案，那我們就可以說這個議案被選定了（

P0已經是一個完備的一致性演算法，保證了P0也就解決了一致性問題。但是P0的實用性不佳，一個議案想被半數以上的Acceptor接受是一件極其困難的事情！

看下面這種情況：A1，A2，A3分別接受了“趙”，“錢”，“孫”，結果沒有任何一個議案形成多數派，所有的議案都將返回“失敗”。議案的數量越多，那議案被選定的概率就越低，這顯然是沒法容忍的。

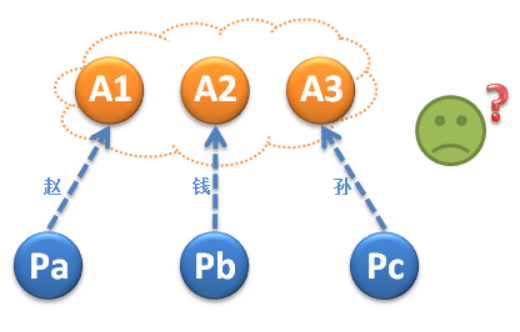
要解決這個問題，必須允許一個Acceptor接受多個議案，後接受的議案可以覆蓋掉之前接受的議案。

如下圖所示， A1已經接受了“趙”，A2已經接受了“錢”，此時Pc提出了“孫”，並被A1，A2，A3接受，這樣就解決了無法形成多數派的問題。

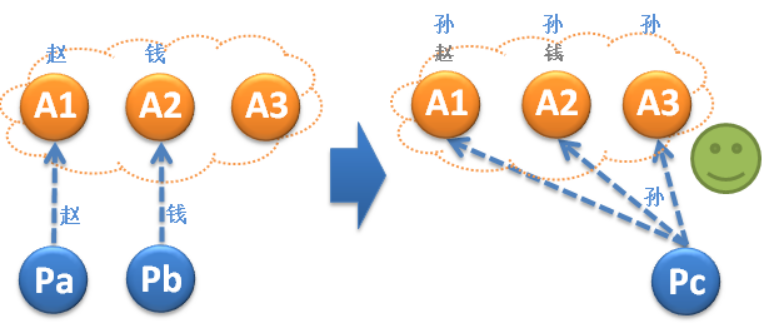
但現在又會面臨下圖中的新問題：A1，A2，A3已經接受了“趙”，此時我們認為“趙”是被選定的，但此時偏偏Pb和Pc不識時務，Pb向A2提出了“錢”，Pc向A3提出了“孫”。這樣就從一致性狀態，又回到了不一致的狀態…這顯然破壞了一致性。

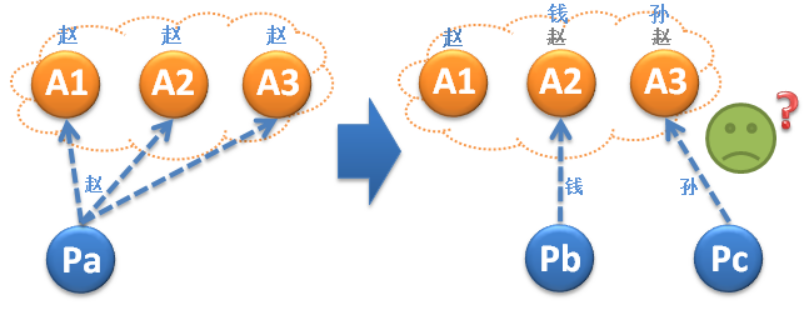
Paxos就是在上述背景下產生的，Paxos要實現的目標的是：

1. 一次選舉必須要選定一個議案（不能出現所有議案都被拒絕的情況）
2. 一次選舉必須只選定一個議案（不能出現兩個議案有不同的值，卻都被選定的情況）

Paxos演算法的推導

首先，Paxos演算法的必須要能滿足第一個條件：

P1：一個Acceptor必須接受它收到的第一個議案。

要滿足這個條件實在太過簡單了，方法略。。。

下面是我個人對這個條件的理解，為什麼必須滿足這個條件：

假設只有一個Acceptor，只有一個Proposer。如果Acceptor出於某些原因拒絕了Proposer的議案，那必然導致Paxos的目標T1無法達成。因此可以認為目標T1隱含了P1。

在開始P2的推導的前，為了區分不同議案，需要先對每個Proposer的議案進行編號，編號時必須保證每個議案的編號具有唯一性（不討論實現方法），而且編號是不斷增大的。

Paxos的目標T2隱含了P2：

P2：如果一個值為v的議案被選定了，那麼被選定的更大編號的議案，它的值必須也是v。

P2很容易理解，除了其中的一個形容詞“更大編號的”，這個形容詞很扎眼，為什麼只對更大編號的議案進行限制，更小的編號怎麼辦？

老頭子給的解釋很簡單“By induction on proposal number”（如果不看論文後半部分，沒人知道他在說什麼…）我說一下我自己的理解：

首先把“更大編號的”幾個字換成“其他的”，我們稱它為P2S。那麼P2S能否滿足Paxos的目標？答案是肯定的。然後比較P2和P2S，誰的約束更強？這得看“更小的編號”是怎麼處理的，從論文後面的推演來看更小編號的議案絕對不允許被選定！！！因此滿足P2的議案是P2S的一個子集。

顯而易見，P2S和P2都能滿足Paxos目標。換句話說，能滿足Paxos目標的辦法很多，但我們只選其中一個辦法就OK了。不過，要選最簡單的辦法（看完後面就知道了）。

總之，現在我們可以得出一個結論：

如果P1和P2都能夠被滿足，那麼Paxos的兩個目標就能夠達成。

如果你對上面這個結論沒有異議，那麼就說明你已經充分理解了P1和P2。

接下來就需要想辦法，如何才能滿足P2：議案在選定前，都要先被Acceptor接受，因此要滿足P2，我們只要滿足下面的條件：

P2a：如果一個值為v的議案被選定了，那麼Acceptor接受的更大編號的議案，它的值必須也是v。

P2a是P2的充分條件，但是P2a存在一個大麻煩：當一個議案被選定後，一部分Acceptor無法立刻獲得通知。例如下圖中A1和A2已經接受了“趙”，這時“趙”就被選定了，此時Pb向A3提出了一個議案“錢”，這是A3接受的第一個議案，為了滿足P1，A3必須接受這個議案，此時就會導致P2a無法被滿足了。

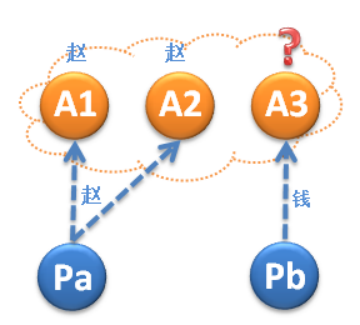
為了解決上述的問題，我們想一下：要是此時不讓Pb提出“錢”這個議案，而是提出“趙”這議案就萬事大吉了。順著這個思路，我們得到了P2b：

P2b：如果一個值為v的議案被選定了，那麼Proposer提出的更大編號的議案，它的值必須也是v。

P2b是一個比P2a更強的約束，也就是說P2b是P2a的充分條件，只要能滿足P2b，那P2a就自動滿足。但P2b很難被滿足，考慮下圖這種情況，A1接受了議案“趙”，A2即將接受議案“趙”，此時Pb提出了一個議案“錢”，這種情況下我們又會遇到跟P2a完全相同的麻煩。

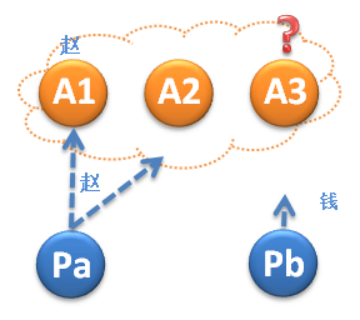
很明顯，要想滿足P2b，我們必需讓Proposer擁有“預測未來”的能力，這聽起來像在講鬼故事，後面會想辦法解決這一點。

在介紹如何“預測未來”之前，我們必須先確定Proposer在提出一個議案時，它的值該如何選取，因為取值的方法決定了“預測”的方法。

一個理所當然的取值方法：找到一個Acceptor的多數派的集合，集合內被接受的議案的值都是v，此時Proposer提出一個新的議案，議案的值必須也是v；如果沒有這樣的多數派集合，那Proposer就任意提。

這個取值方法，完全能符合P2b，這是一目瞭然的，但問題出在 “預測”上，我們必須能預測到即將形成多數派的那個議案，如果有誰能做到那就真的是在講鬼故事了。

Proposal提出議案的正確姿勢：

P2c：在所有Acceptor中，任意選取半數以上的Acceptor集合，我們稱這個集合為S。Proposal新提出的議案（簡稱Pnew）必須符合下面兩個條件之一：

1） 如果S中所有Acceptor都沒有接受過議案的話，那麼Pnew的編號保證唯一性和遞增即可，Pnew的值可以是任意值。

2） 如果S中有一個或多個Acceptor曾經接受過議案的話，要先找出其中編號最大的那個議案，假設它的編號為N，值為V。那麼Pnew的編號必須大於N，Pnew的值必須等於V。

P2c提出議案的規則有點複雜，它真的能滿足P2b嗎？至少看上去不是那麼一目瞭然…..老頭子用了歸納法來證明P2c能滿足P2b，但效果不佳，沒什麼人能看懂，所以下面的證明過程即使你看不懂也必要太沮喪（後面會給出圖文解釋）。

證明題（注意！前方高能）：

已知議案是集合中第一個被選定的議案，接受這個議案的Acceptor集合為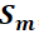，在滿足P2c的規則2的情況下，提出了一個新的議案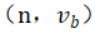，n>m，證明

第一步，證明初始成立：當議案的編號n = m+1時，證明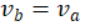

因為是第一個被選定的議案，因此在m+1提出之前，m必然是叢集當中編號最大的議案。

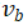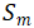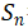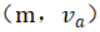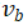根據P2c的規則2，議案能夠被提出，是因為存在一個多數派集合，這個集合中，編號最大的議案的值為。因為和都是多數派集合，所以他們必定存在交集。交集中的Acceptor必定都接受了。m是整個叢集最大的編號，當然也就是中最大的編號，根據P2c的規則2，必定等於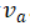

第二步，當n > m+1時，假設編號從m+1到n-1的議案的值都是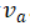，證明：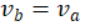

編號為m+1到n-1的議案提出後，我們沒辦法判斷究竟那一個議案會被選定，但有一點是可以肯定的：所有接受了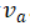的Acceptor構成了一個新的集合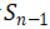，這個集合包含了集合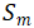中的所有Acceptor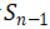，顯然是一個多數派集合，這個集合接受的議案的編號在m到n-1之間，而且值為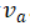。沒有包含在集合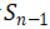中的Acceptor所接受的議案一定小於m。

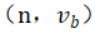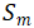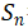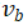根據P2c的規則2，議案能夠被提出，那麼一定存在一個多數派集合，因為和都是多數派集合，所以他們必定存在交集。交集中的議案的最大編號一定大於等於m，小於等於n-1。因此集合中編號最大的議案一定位於交集內。根據P2c的規則，必定等於。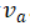

這個證明過程，如果你能看懂，請受我三跪。。。

接下來，上圖，舉例說明。

假設有一個議案（3，Va）提交後，這個議案成為了被Acceptor叢集選定的第一個議案 ，那此時叢集的狀態可能會如下圖所示：

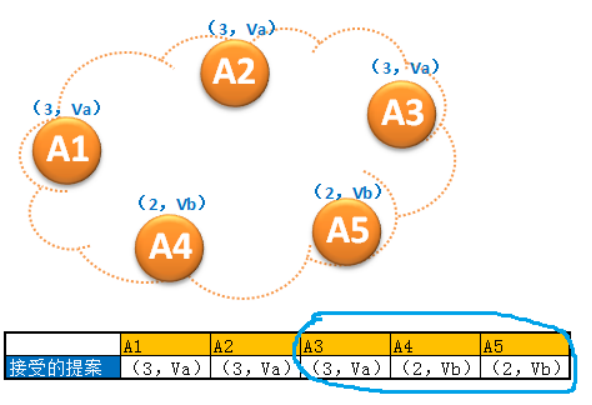
一共5個Acceptor，有3個Acceptor接受了議案（3，Va），剛剛過半。此時有一個編號為4的議案要提出，根據P2c的規則2，首先選一個過半的集合，就選上圖中藍色線圈出來的A3，A4，A5好了（任意選），這個集合中編號最大的議案是（3，Va），因此新提出的議案必定為（4，Va）。符合P2b。

議案（4，Va）提出後，叢集的狀態可能是下面這樣：

此時再提出編號為5或6，7，8，9，10的議案，這個議案的值必定也是Va（不信的話請舉出反例），符合P2b。依此類推。。。

由此可證，P2c是能夠滿足P2b的！！！

想想看P2，P2a，P2b中為什麼一定要有“更大編號的”這幾個扎眼的字眼，此時你應該能有一點感覺了，可能你會把它理解成“後提出的”，如果你是這樣理解的話，請往下看。

有些童鞋肯定早就已經想到了：當議案（3，Va）提交後，這個議案成為了被Acceptor叢集選定的第一個議案，此時叢集的狀態有沒有可能是下面這樣？

注意，這時議案（4，Vb）才是叢集當中的編號最大的議案，要是這樣就糟糕了！當我們提出編號為5的議案時，它的取值就有可能是Vb，導致無法滿足P2b。

為了保證不出現這種情況，就要用到前面提到的“預測未來”的能力。跟P2c的議案規則相配套的，需要預測的未來是：

當一個議案在提出時（即使已經在傳送的半路上了），它必須能夠知道當前已經提出的議案的最大編號。

這樣的話，議案（3，Va）提交時，就會知道有一個（4，Vb）的議案已經提交了，然後將自己的編號改成5或更大編號提交，一切就完美了。

但是你知道的，我們並不可能真的預測未來，換個思路，議案肯定是要提交給Acceptor的，只要由Acceptor來保證議案編號的順序就OK了。於是有：

議案（n，v）在提出前，必須將自己的編號通知給半數以上的Acceptor。收到通知的Acceptor將n跟自己之前收到的通知進行比較，如果n更大，就將n確認為最大編號。當半數以上Acceptor確認n是最大編號時，議案（n，v）才能正式提交。

兩個編號不同的議案，不可能同時被確認為最大編號，證明略。

但是實際環境上，上面的條件還不足以保證議案被接受的順序，比如議案（n，Va）被確認為最大編號後，開始向Acceptor傳送，此時（n+1，Vb）提出，由於網路速度的原因，（n+1，Vb）可能比（n，Va）更早被Acceptor接收到。

因此Acceptor收到一個新的編號n，在確認n比自己之前收到的編號大時，必須做出承諾（Promise）：不再接受比n小的議案。

這個承諾會導致部分漏網之魚（在傳送途中被搶走最大編號的議案），無法形成多數派。

例如下圖所示：有一個在途的議案（1，Va），當A2和A3對議案（2，Vb）做出承諾的同時，（1，Va）就失去了形成多數派的權利。

至此，我們就形成了一個完整的演算法（具體實現請自行搜尋PhxPaxos）。

後記

演算法原文中，將Promise看做是P2c的具體實現，而我們將Promise看成是彌補P2c的補充條件。這兩者沒有質的差別，只是角度不同，我個人認為後一種更容易被理解，所以採用了後一種。不過採用後一種會遇到下面的麻煩：

按下面的順序提交議案：

① 議案（1，Va）向A1傳送Prepare，獲得A1的承諾。

② 議案（2，Vb）向A1傳送Prepare，獲得A1的承諾。

③ 傳送議案（1，Va）

此時A1會拒絕議案（1，Va）

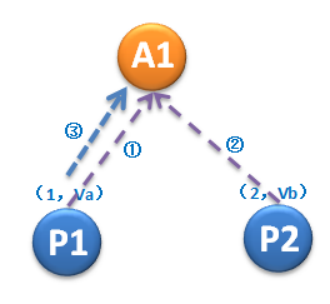
採用後一種解釋的話，會發現A1拒絕議案（1，Va）是違反了P1的，而採用前一種解釋則不違反P1。（這不過是個文字遊戲，我已經懶的去思考了，就這樣吧）

如果我們將半數以上的Acceptor對同一個議案（n，v）做出承諾的狀態稱作是“鎖定”狀態。那麼這個“鎖定”狀態具有以下性質：

排它性：所有比n小的議案都不允許提交，已經在途的議案，則不允許其形成多數派。

唯一性：任意時刻，全域性只有一個議案能獲得“鎖定”狀態。

原子性：議案n從鎖定狀態變為非鎖定狀態的過程是原子的，議案n+1從非鎖定狀態變更為鎖定狀態的過程也是原子的。

我相信（有點虛…），正是上面的這三條性質保證了一致性。

最後，感謝老頭子給出的如此精彩的演算法。