正態分佈&&切比雪夫不等式
阿新 • • 發佈:2018-12-23
百度百科:https://baike.baidu.com/item/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83/829892?fr=aladdin
知乎:https://www.zhihu.com/question/27821324一維正態分佈
若 隨機變數標準正態分佈
當
性質
正態分佈的一些性質: [2] (1)如果切比雪夫不等式,描述了這樣一個事實,事件大多會集中在平均值附近。
2.1 切比雪夫不等式與直觀感受
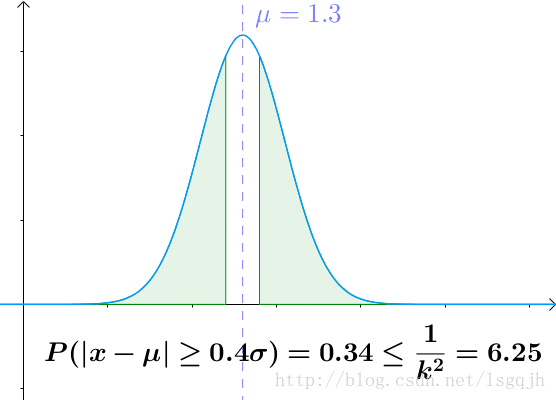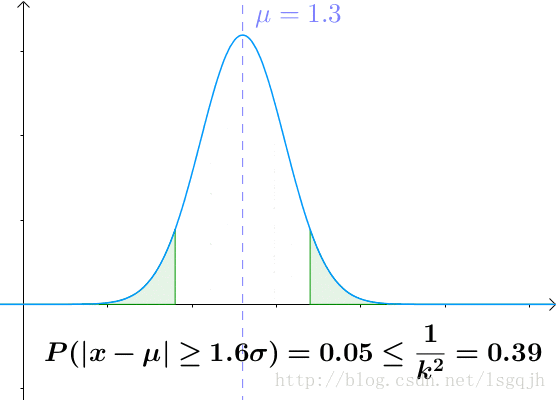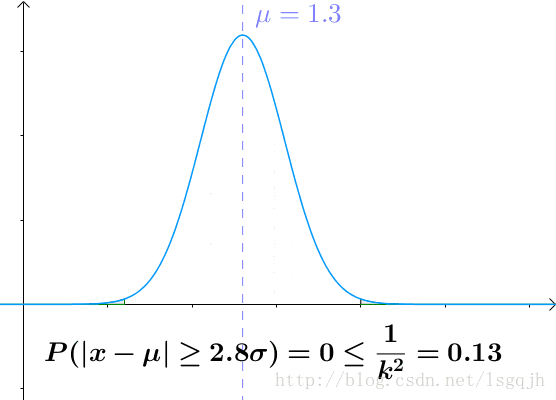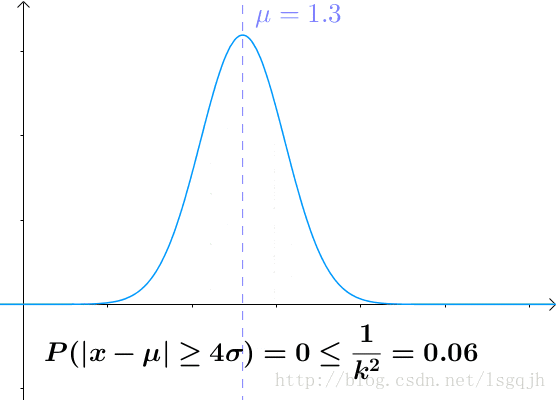
切比雪夫不等式是這麼寫的:
其中 ,
是期望,
是標準差。
我們還是通過 的正態分佈來感受一下切比雪夫不等式:可見,越遠離平均值,概率越低。
2.2切比雪夫不等式的證明
馬爾科夫不等式是這樣的:
我們把 代入:
很顯然等價於:
令 ,容易得到
: