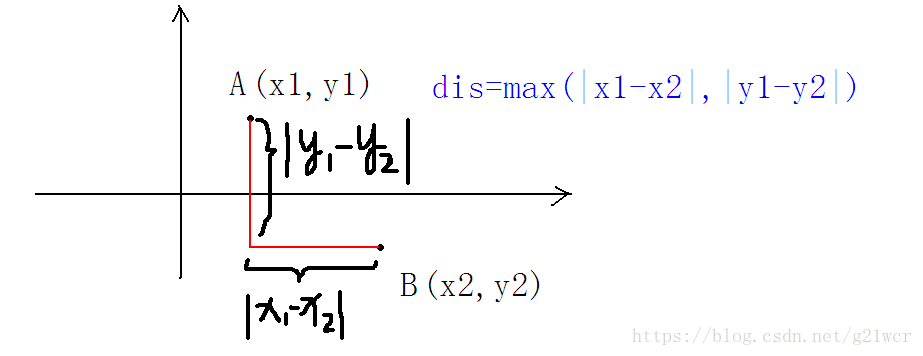【感謝xly苣銠】

【曼哈頓距離】

【切比雪夫距離】

【關於兩者的關係】

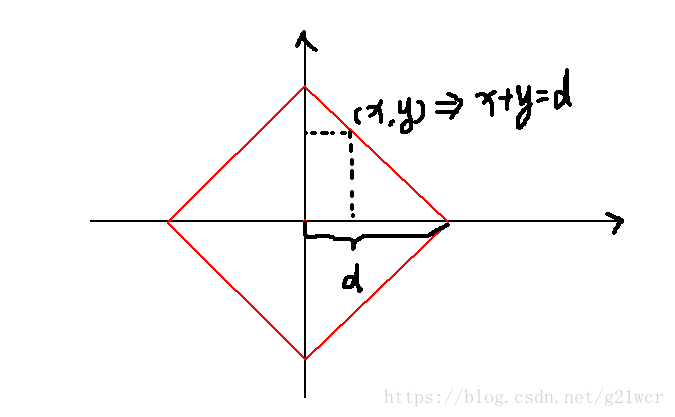
距離原點曼哈頓距離為d的點集如下圖：它們在紅色的菱形上。

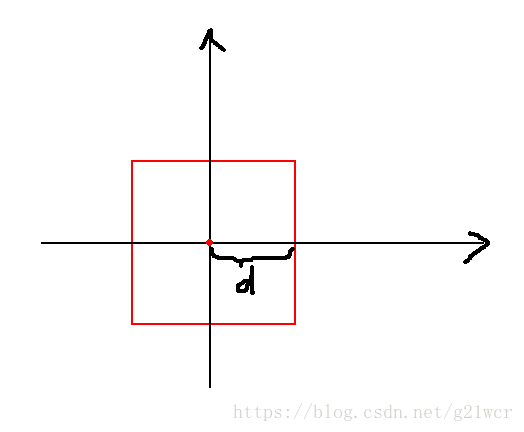
距離原點切比雪夫距離為d的點集如下圖：它們在紅色的正方形上。

這兩個圖好像很像啊。其實這兩者是可以相互轉化的。

對於兩個點A(x1,y1),B(x2,y2)

曼哈頓距離：|x1-x2|+|y1-y2|    ——>    max{  x1-x2+y1-y2  ,  x2-x1+y1-y2  ,  x1-x2+y2-y1  ,  x2-x1+y2-y1}

【把絕對值拆開的所有情況，四個中有一個是正確的值。其他錯誤的值的兩個部分中至少有一個是負的，而正確的值兩個部分都是正的，那麼在這四個可能情況中取個max就得到了這個正確的值，也就是曼哈頓距離】

切比雪夫距離：max{|x1-x2|,|y1-y2|}

考慮(x1+y1,x1-y1)和(x2+y2,x2-y2)

這兩個點的切比雪夫距離為max{|x1+y1-x2-y2|,|x1-y1-x2+y2|}

把這個絕對值拆一下就跟上面曼哈頓距離相同了。這時，就成功地把兩個點的切比雪夫距離轉化為了曼哈頓距離。

【哈哈，其實前面的口胡都不用看，記住結論就行了】

將一個點(x,y)的座標變為(x-y,x+y)後，原座標系下的切比雪夫距離就變成了現座標系下的曼哈頓距離。

將一個點(x,y)的座標變為((x+y)/2,(x-y)/2)後，原座標系下的曼哈頓距離就變成了現座標系下的切比雪夫距離。

一個弱弱的題解    一個洛谷的例題