Codeforces Div2 F. Mars rover
F. Mars rover
time limit per test
5 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
Natasha travels around Mars in the Mars rover. But suddenly it broke down, namely — the logical scheme inside it. The scheme is an undirected tree (connected acyclic graph) with a root in the vertex 1
, in which every leaf (excluding root) is an input, and all other vertices are logical elements, including the root, which is output. One bit is fed to each input. One bit is returned at the output.
There are four types of logical elements: AND (2
inputs), OR (2 inputs), XOR (2 inputs), NOT (1
input). Logical elements take values from their direct descendants (inputs) and return the result of the function they perform. Natasha knows the logical scheme of the Mars rover, as well as the fact that only one input is broken. In order to fix the Mars rover, she needs to change the value on this input.
For each input, determine what the output will be if Natasha changes this input.
Input
The first line contains a single integer n
(2≤n≤106
) — the number of vertices in the graph (both inputs and elements).
The i
-th of the next n lines contains a description of i-th vertex: the first word "AND", "OR", "XOR", "NOT" or "IN" (means the input of the scheme) is the vertex type. If this vertex is "IN", then the value of this input follows (0 or 1), otherwise follow the indices of input vertices of this element: "AND", "OR", "XOR" have 2 inputs, whereas "NOT" has 1
input. The vertices are numbered from one.
It is guaranteed that input data contains a correct logical scheme with an output produced by the vertex 1
.
Output
Print a string of characters '0' and '1' (without quotes) — answers to the problem for each input in the ascending order of their vertex indices.
Example
Input
Copy
10 AND 9 4 IN 1 IN 1 XOR 6 5 AND 3 7 IN 0 NOT 10 IN 1 IN 1 AND 2 8
Output
Copy
10110
Note
The original scheme from the example (before the input is changed):
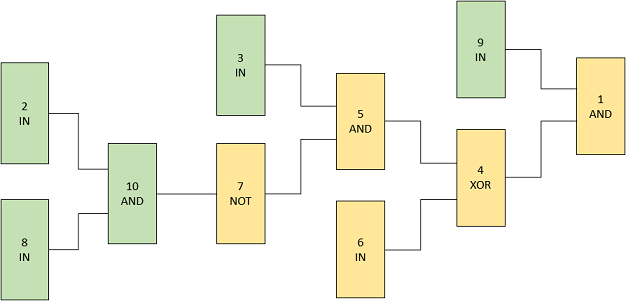
Green indicates bits '1', yellow indicates bits '0'.
If Natasha changes the input bit 2
to 0, then the output will be 1
.
If Natasha changes the input bit 3
to 0, then the output will be 0
.
If Natasha changes the input bit 6
to 1, then the output will be 1
.
If Natasha changes the input bit 8
to 0, then the output will be 1
.
If Natasha changes the input bit 9
to 0, then the output will be 0.
題意:
就是給出一顆樹, 變換各個IN的值, 求根節點的值。
一開始想用模擬, 發現TLE。 。然後在別人的細心教誨下終於明白了寫。
( 1)先求根節點的值。
( 2)然後從根節點進行搜尋。
這裡分5種情況。
( 1)當為AND時: 先看看此節點的值, 如果為1,那麼改變任意一個子節點的值,都不會改變根節點的值, 所以繼續搜尋左右子樹。如果為0:那麼此時左右子樹肯定至少有一個必為0,1.如果有一個為0,只有當為0的點改變值時,才會影響根節點,所以搜尋為0的子樹。2.如果都為0,那麼改變其中一個值不會影響根節點。所以直接返回。
(2)當為OR時: 跟上面的情況很像,當為0時, 這時兩個子樹的改變都會影響根節點的值, 需要都進行搜尋。
當為一的時候, 有三種情況, 當兩個子樹都為1時, 這種情況直接return。 當一個為0, 一個為1時, 為0的子樹不會影響根節點的值, 而1的節點的改變會影響根節點的值, 所以這時候需要搜尋1的子樹。
(3) 當為異或時, 只要改變一個子樹的值, 那麼根節點的值必定改變, 所以需要搜尋兩顆子樹。
( 4)當為NOT時, 只要改變子節點的值,根節點的值必定改變, 所以需要搜尋。
( 5)當為IN時, 說明這個子節點會影響到根的值。 所以需要取反。
程式碼如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
struct node
{
char s[10];
int left,right;
int data;
int parent;
int in;
};
node no[1000005];
int n;
int par;
int change[1000005];
int ch=0;
int re;
int dfs (int loc)
{
if(!strcmp(no[loc].s,"IN"))
return no[loc].data;
else if(!strcmp(no[loc].s,"AND"))
{
no[loc].data=(dfs(no[loc].left)&dfs(no[loc].right));
return no[loc].data;
}
else if(!strcmp(no[loc].s,"XOR"))
{
no[loc].data=(dfs(no[loc].left)^dfs(no[loc].right));
return no[loc].data;
}
else if(!strcmp(no[loc].s,"NOT"))
{
no[loc].data=(!dfs(no[loc].left));
return no[loc].data;
}
else if(!strcmp(no[loc].s,"OR"))
{
no[loc].data=dfs(no[loc].left)|dfs(no[loc].right);
return no[loc].data;
}
}
void dfs1 (int loc)
{
if(!strcmp(no[loc].s,"IN"))
{
no[loc].in=1;
no[loc].data=1^re;
}
else if(!strcmp(no[loc].s,"AND"))
{
if(!no[loc].data)
{
if(!no[no[loc].left].data&&!no[no[loc].right].data)
return ;
else if(!no[no[loc].left].data)
dfs1(no[loc].left);
else if(!no[no[loc].right].data)
dfs1(no[loc].right);
}
else
{
dfs1(no[loc].left);
dfs1(no[loc].right);
}
}
else if(!strcmp(no[loc].s,"OR"))
{
if(no[loc].data)
{
if(no[no[loc].left].data&&no[no[loc].right].data)
return;
else if(no[no[loc].left].data)
dfs1(no[loc].left);
else if(no[no[loc].right].data)
dfs1(no[loc].right);
}
else
{
dfs1(no[loc].left);
dfs1(no[loc].right);
}
}
else if(!strcmp(no[loc].s,"XOR"))
{
dfs1(no[loc].left);
dfs1(no[loc].right);
}
else if(!strcmp(no[loc].s,"NOT"))
dfs1(no[loc].left);
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n+3;i++)
{
no[i].parent=-1;
no[i].data=-1;
no[i].in=0;
}
for (int i=1;i<=n;i++)
{
int left,right;
scanf("%s",no[i].s);
if(!strcmp(no[i].s,"AND"))
{
scanf("%d%d",&left,&right);
no[left].parent=i;
no[right].parent=i;
no[i].left=left;
no[i].right=right;
}
if(!strcmp(no[i].s,"IN"))
{
scanf("%d",&no[i].data);
no[i].left=no[i].right=-1;
}
if(!strcmp(no[i].s,"XOR"))
{
scanf("%d%d",&left,&right);
no[left].parent=i;
no[right].parent=i;
no[i].left=left;
no[i].right=right;
}
if(!strcmp(no[i].s,"NOT"))
{
scanf("%d",&left);
no[left].parent=i;
no[i].left=left;
no[i].right=-1;
}
if(!strcmp(no[i].s,"OR"))
{
scanf("%d%d",&left,&right);
no[left].parent=i;
no[right].parent=i;
no[i].left=left;
no[i].right=right;
}
}
for (int i=1;i<=n;i++)
if(no[i].parent==-1)
{
par=i;
break;
}
re=dfs(par);
dfs1(par);
for (int i=1;i<=n;i++)
{
if(no[i].s[0]=='I')
{
if(no[i].in)
printf("%d",no[i].data);
else
printf("%d",re);
}
}
printf("\n");
return 0;
}
