2. 程式人生 > >ACM-ICPC 2017南寧賽區網路賽題目題解收集

ACM-ICPC 2017南寧賽區網路賽題目題解收集

阿新 • • 發佈：2018-12-24

前言：本篇文章的主要程式碼來自於CSDN部落格或者網路，感謝網路ACMdalao的AC程式碼，佩服他們，本文最後會寫出各個AC程式碼的原作者和網址。（注意一點，每個程式的標頭檔案我都改成了萬能標頭檔案，測試時間可能會加長，如果需要原始碼的標頭檔案請直接在程式碼後面的連結裡面去找一下，我喜歡C++裡面不用類似於stdio.h的標頭檔案寫法的標頭檔案，我可能會寫成cstdio，注意，萬能標頭檔案在POJ裡面是不能識別的，會出現CE，這個時候你就需要修改萬能標頭檔案成你所需要的標頭檔案）
ACM-ICPC 2017南寧賽區網路賽題目及其題解
題目列表

  • A.Weather Patterns
  • B.Train Seats Reservation
  • C.Auction Bidding
  • D.Path Search with Constraints
  • E.Visible Surface
  • F.Overlapping Rectangles
  • G.Finding the Radius for an Inserted Circle
  • H.A Cache Simulator
  • I.GSM Base Station Identification
  • J.Minimun Distance in a Star Graph
  • K.Line Segments Clipped by Windows
  • L.The Heaviest Non-decreasing Subsequence Problem
  • M.Frequent Subsets Problem
    下面開始單個題目的題目內容和解析程式碼。
    A.Weather Patterns（數學期望+英語閱讀理解）
    題目連結：https://nanti.jisuanke.com/t/17308
    PS：看了之後感覺，學好英語很重要，這道題主要考察ACMer的英語閱讀理解能力，題目本身是不難，但是英語理解需要一點能力。真的當時被坑了。
    題意：這題一點都不難，一道英語閱讀理解題，讀懂了你就會做了！這道題其實就是每天會有四種天氣，分別是①下雪②下雨③多雲④晴天，然後給你一個4*4的矩陣，這個矩陣的第i行第j個表示的就是從天氣i到天氣j的概率，然後接下來給你兩個觀察序列，問你天氣完全按照這個觀察序列上的順序變化的概率是多少，第一天是任何天氣的概率都為1。接下來再給你兩個數i和j，問連續數天都是i天氣和j天氣的數學期望分別是多少。
    思路：
    對於任意一個觀察序列，我們只要按序列的順序把兩個天氣之間變化的概率不斷地乘就可以得出答案，比如說題目中的第二個序列，2 1 1 1 3 3 4，那麼a[2][1]*a[1][1]*a[1][1]*a[1][3]*a[3][3]*a[3][4]就是答案。對於數學期望，我們就是求連續1天是i天氣的概率+連續2天是i天氣的概率+……+連續n天是i天氣的概率，雖然這個n是無限大的，但是當加到後面之後這個概率會非常小可以忽視，所以我們只需要加1000個差不多就夠了。
    程式碼如下：
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int INF = 1e9 + 5;
const int MAXN = 100000007;
const int MOD = 1e9 + 7;
const double eps = 1e-8;
const double PI = acos(-1.0);
LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a%b); }


double MA[5][5];

int main()
{
    double ans, res;
    int x, y;
    char ch;
    for (int i = 1; i <= 4; i++)
        for (int j = 1; j <= 4; j++)
            scanf("%lf", &MA[i][j]);
    ans = 1;
    getchar();
    y = -1;
    while (scanf("%d", &x))
    {
        if (y == -1)
        {
            y = x;
            continue;
        }
        else
        {
            ans *= MA[y][x];
            y = x;
        }
        ch = getchar();
        if (ch != ' ')
            break;
    }
    printf("%.8f\n", ans);
    y = -1;
    ans = 1;
    while (scanf("%d", &x))
    {
        if (y == -1)
        {
            y = x;
            continue;
        }
        else
        {
            ans *= MA[y][x];
            y = x;
        }
        ch = getchar();
        if (ch != ' ')
            break;
    }
    printf("%.8f\n", ans);
    scanf("%d", &x);
    ans = 0;
    res = 1;
    for (int i = 1; i <= 1000; i++)
    {
        ans += res;
        res *= MA[x][x];
    }
    printf("%.8f\n", ans);
    scanf("%d", &x);
    ans = 0;
    res = 1;
    for (int i = 1; i <= 1000; i++)
    {
        ans += res;
        res *= MA[x][x];
    }
    printf("%.8f\n", ans);
}

B.Train Seats Reservation（暴力遍歷）
題目連結：https://nanti.jisuanke.com/t/17309
題意：一輛火車從1開到n，給你幾個從l上車，r下車的人數。讓你求這輛火車至少要裝多少座位才可以都坐下。
POINT：
資料很小，暴力，求區間1到n裡同時人數最多的就行。注意r這個點的人是要下車的，可以同時上車。
程式碼如下：

#include <bits/stdc++.h>
using namespace std;
#define LL long long
const LL maxn = 111;
LL a[maxn];
int main()
{
    LL n;
    while(~scanf("%lld",&n))
    {
        if(n==0)
        {
            printf("*\n");
            break;
        }
        memset(a,0,sizeof a);
        LL ans=0;
        LL l,r,k;
        for(LL j=1;j<=n;j++){
        scanf("%lld %lld %lld",&l,&r,&k);
            if(l>r) swap(l, r);
        for(LL i=l;i<r;i++)
        {
            a[i]+=k;
            if(ans<a[i]) ans=a[i];
        }
        }
        printf("%lld\n",ans);

    }
}

C.Auction Bidding
題目連結：https://nanti.jisuanke.com/t/17310
本題暫時沒找到AC程式碼，待補
D.Path Search with Constraints
題目連結：https://nanti.jisuanke.com/t/17311
本題暫時沒找到AC程式碼，待補
E.Visible Surface
題目連結：https://nanti.jisuanke.com/t/17312
本題暫時沒找到AC程式碼，待補
F.Overlapping Rectangles（離散+線段樹，需要離散數學和資料結構的知識）
題目連結：https://nanti.jisuanke.com/t/17313
題意：計算矩形面積並
思路：主要用到了離散數學+線段樹的知識，有模板的可以直接套用模板，然後修改一下就能過
PS：這道題我們隊原來就沒想著過，結果我們隊的一個dalao直接用模板就AC了O(∩_∩)O哈哈~，當時就吃驚了，因為那個時候我們在死磕B（說句實話，我們的B花的時間太多了T^T，主要是想複雜了）
附上原作者的AC程式碼：

#include<bits/stdc++.h>
using namespace std;
#define LL long long
const LL maxn = 1111;
#define lt x<<1
#define rt x<<1|1
LL a[maxn];
struct len
{
    int l,r;
    int kind;
    int h;
}l[maxn*2];
struct ju
{
    int a,b,c,d;
}z[maxn];
int p[maxn*2],num;
int pp[maxn*2];
int sum[maxn*8];
int add[maxn*8];
bool cmd(len a,len b)
{
 //   if(a.h!=b.h)
    return a.h<b.h;
}
void pushdown(int x,int l,int r)
{
    sum[lt]+=add[x];
    add[lt]+=add[x];
    sum[rt]+=add[x];
    add[rt]+=add[x];
    add[x]=0;
}
void change(int x,int l,int r,int ll,int rr,int kind)
{
    if(add[x]!=0)
    {
        pushdown(x,l,r);
    }
    if(ll<=l&&rr>=r)
    {
        add[x]=kind;
        sum[x]+=kind;
    }
    else
    {
        int mid=(l+r)>>1;
        if(ll<=mid)
        {
            change(lt,l,mid,ll,rr,kind);
        }
        if(mid<rr)
        {
            change(rt,mid+1,r,ll,rr,kind);
        }
    }
}
int query(int x,int l,int r)
{
    if(add[x]) pushdown(x, l, r);
    int ans=0;
    if(l==r)
    {
        if(r==num) return 0;
        if(sum[x]>0)
            ans+=p[r+1]-p[l];
    }
    else
    {
        int mid=(l+r)>>1;
        ans+=query(lt,l,mid);
        ans+=query(rt,mid+1,r);
    }
    return ans;

}
int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        if(n==0)
        {
            printf("*");
            break;
        }
        num=0;
        for(int i=1;i<=n;i++)
        {
            scanf("%d %d %d %d",&z[i].a,&z[i].b,&z[i].c,&z[i].d);
            pp[++num]=z[i].a;
            pp[++num]=z[i].c;
        }
        sort(pp+1,pp+1+num);
        for(int i=1;i<=num;i++)
        {
            p[i]=pp[i];
        }
        int lennum=0;
        for(int i=1;i<=n;i++)
        {
            l[++lennum].l=lower_bound(pp+1,pp+1+num,z[i].a)-pp;
            l[lennum].r=lower_bound(pp+1,pp+1+num,z[i].c)-pp;
            l[lennum].kind=1;
            l[lennum].h=z[i].b;
            l[++lennum].l=lower_bound(pp+1,pp+1+num,z[i].a)-pp;
            l[lennum].r=lower_bound(pp+1,pp+1+num,z[i].c)-pp;
            l[lennum].kind=-1;
            l[lennum].h=z[i].d;
        }
        sort(l+1,l+1+lennum,cmd);
        memset(sum,0,sizeof sum);
        memset(add,0,sizeof add);
        int ans=0;
        for(int i=1;i<=lennum;i++)
        {
            int temp=query(1, 1, num);
            if(i>=2)
            {
                ans+=temp*(l[i].h-l[i-1].h);
            }
            change(1,1,num,l[i].l,l[i].r-1,l[i].kind);

        }
        printf("%d\n",ans);


    }
}

G.Finding the Radius for an Inserted Circle（運算幾何，二分）
題目連結：https://nanti.jisuanke.com/t/17314
這道題需要數學知識，具體看下面。
題意：這道題就是給你三個一模一樣的圓，左邊一個右邊一個下面一個，三個圓兩兩相切，然後在這三個圓中間的地方找一個小圓，要求這個小圓與這三個大圓相切，這被稱為一次操作，然後第二次操作的時候，就把下面的大圓替換成那個小圓，然後從這兩個大圓和一個小圓中間再找一個更小的圓也與它們相切，最後問你經過k次操作後那個小圓的半徑是多少。
思路：我們可以把三個圓的圓心兩兩相連，連成一個三角形，再把三個圓心與中間的小圓心相連，假設左右兩個大圓的半徑為R，下面的圓半徑為r，中間的小圓半徑為s，那麼就可以轉化成下圖。
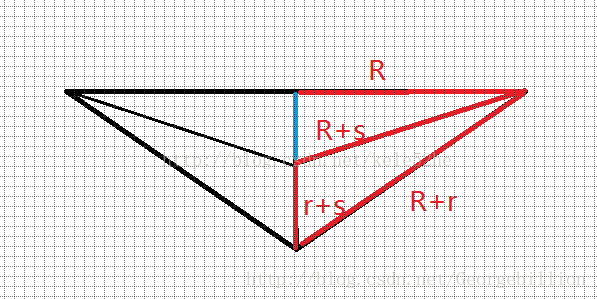
這裡寫圖片描述
紅色的邊都是已知長度的，並且長度都在圖中標記了出來，因為相切，所以兩圓心的距離等於兩圓半徑之和。
那麼我們可以對圖中的藍色邊做文章，藍色邊的長度可以等於sqrt((R+s)^2-R^2)，也可以等於sqrt((R+r)^2-R^2)-r-s。這樣我們讓這兩個等式相等，就可以通過R和r求出s了，不過這個方程組裡有根號，不是很好解，所以我們可以用二分的方法去尋找方程的解。s求出來後我們就完成了一次操作，然後把s的值賦給r，我們就可以進行第二次操作了。
PS：這道題本來我想先A的，結果看看有點複雜就沒上手，賽後一看，炸了，幾何題，瞬間爆炸，想打死自己了
下面是AC程式碼：（瞬間感覺自己數學要重學了）


#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int INF = 1e9 + 5;
const int MAXN = 100000007;
const int MOD = 1e9 + 7;
const double eps = 1e-8;
const double PI = acos(-1.0);
LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a%b); }

struct POINT
{
    double x;
    double y;
    POINT(double a = 0, double b = 0) { x = a; y = b; } //constructor 
};

struct LINESEG
{
    POINT s;
    POINT e;
    LINESEG(POINT a, POINT b) { s = a; e = b; }
    LINESEG() { }
};

double multiply(POINT sp, POINT ep, POINT op)
{
    return((sp.x - op.x)*(ep.y - op.y) - (ep.x - op.x)*(sp.y - op.y));
}

bool InsideConvexPolygon(int vcount, POINT polygon[], POINT q) // 可用於三角形！ 
{
    POINT p;
    LINESEG l;
    int i;
    p.x = 0; p.y = 0;
    for (i = 0; i<vcount; i++) // 尋找一個肯定在多邊形polygon內的點p：多邊形頂點平均值 
    {
        p.x += polygon[i].x;
        p.y += polygon[i].y;
    }
    p.x /= vcount;
    p.y /= vcount;

    for (i = 0; i<vcount; i++)
    {
        l.s = polygon[i]; l.e = polygon[(i + 1) % vcount];
        if (multiply(p, l.e, l.s)*multiply(q, l.e, l.s)<0) /* 點p和點q在邊l的兩側，說明點q肯定在多邊形外 */
            break;
    }
    return (i == vcount);
}

void find(int x, int y, int &X, int &Y)
{
    double ox, oy;
    POINT pp[6];
    for (int i = -9; i <= 10; i++)
        for (int j = -9; j <= 10; j++)
        {
            oy = 7.5*j;
            ox = 5 * sqrt(3)*i + j*2.5*sqrt(3);
            pp[0].x = ox;
            pp[0].y = oy + 5;
            pp[1].x = ox + 2.5*sqrt(3);
            pp[1].y = oy + 2.5;
            pp[2].x = ox + 2.5*sqrt(3);
            pp[2].y = oy - 2.5;
            pp[3].x = ox;
            pp[3].y = oy - 5;
            pp[4].x = ox - 2.5*sqrt(3);
            pp[4].y = oy + 2.5;
            pp[5].x = ox - 2.5*sqrt(3);
            pp[5].y = oy - 2.5;
            if (InsideConvexPolygon(6, pp, POINT(x, y)))
            {
                X = i;
                Y = j;
                return;
            }
        }
}

int main()
{
    int x, y;
    int X, Y;
    scanf("%d%d", &x, &y);
    find(x, y, X, Y);
    printf("[%d,%d]", X, Y);
    for (int i = 2; i <= 10; i++)
    {
        scanf("%d%d", &x, &y);
        find(x, y, X, Y);
        printf(", [%d,%d]", X, Y);
    }
    printf("\n");
}

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

ll a[(1<<6)+1];

char s[100];

int main()
{

//    freopen("data.txt","r",stdin);
//    ios_base::sync_with_stdio(false);
    ll ct=0,ct1=0;
    for(int i=0;i<(1<<6);i++)
    {
        a[i]=-1;
    }
    while(~scanf("%s",s))
    {
        if(strcmp(s,"END")==0)
            break;
        ct++;
        int len=strlen(s);
        ll sum=0;
        ll t = 1;
        for(int i=len-1;i>=0;i--)
        {
            if(s[i]>='0'&&s[i]<='9')
            {
                sum += (s[i]-48)*t;
            }
            else if(s[i]>='A'&&s[i]<='F')
            {
                sum += (s[i]-55)*t;
            }
            t*=16;
        }
//        cout << sum<<endl;
        ll t1 = sum/(1<<10);
        sum%=(1<<10);

        ll tt = sum>>4;
        sum%=64;

        if(a[tt]==-1)
        {
            printf("Miss\n");
            a[tt] =t1;
        }
        else
        {
            if(a[tt]==t1)
            {
                ct1++;
                printf("Hit\n");

            }
            else
            {
                printf("Miss\n");
                a[tt] =t1;
            }
        }
    }
    printf("Hit ratio = %.2lf%%\n",(double)ct1/(double)ct*100);
    return 0;
}

感謝chudongfang2015大佬的AC程式碼，給出原連結地址：
http://blog.csdn.net/chudongfang2015/article/details/78080214
I.GSM Base Station Identification（暴力+計算幾何）
題目連結：https://nanti.jisuanke.com/t/17316
PS：這道題是我第一個想寫的題目，一看就感覺像三角定位法，結果一看不對，是六邊形，瞬間腦子一片空白，然後讀到最後感覺有點暈，就沒寫下去，賽後問了大佬之後，我還是感覺自己太naive了，居然可以暴力，瞬間炸了。
題意：有一個座標系，每格的長度是5，然後在這個座標系中有許多邊長為5的正六邊形，這些正六邊形互相連線，沒有空隙，每個正六邊形都有一個自己的座標，原點處的正六邊形座標是[0,0]，然後每往右一個橫座標+1，每往左一個橫座標-1。然後右上方的縱座標+1，左下方的縱座標-1。這樣每個正六邊形都有屬於自己的不同的座標。現在給你一個座標系中的座標，問這個座標所在的正六邊形的座標是多少。
思路：因為正六邊形的橫座標和縱座標的範圍都是[-9,10]，一共只有400個正六邊形，所以我們可以把每一個正六邊形都迴圈一遍，判斷當前的這個點是否在該六邊形中。現在的問題就是我們怎麼判斷這個點是否在座標為[i,j]的正六邊形中，我們首先可以根據i和j求出該正六邊形的中心座標，仔細觀察後可以發現，oy=7.5*j，ox=5*sqrt(3)*i+2.5*sqrt(3)*j。然後我們可以根據中心的座標求出周圍六個頂點的座標，之後我們就可以套用判斷一個點是否在一個凸多邊形內的模板，如果它在裡面，那麼當前的i和j就是答案座標。
程式碼如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int INF = 1e9 + 5;
const int MAXN = 100000007;
const int MOD = 1e9 + 7;
const double eps = 1e-8;
const double PI = acos(-1.0);
LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a%b); }

struct POINT
{
    double x;
    double y;
    POINT(double a = 0, double b = 0) { x = a; y = b; } //constructor 
};

struct LINESEG
{
    POINT s;
    POINT e;
    LINESEG(POINT a, POINT b) { s = a; e = b; }
    LINESEG() { }
};

double multiply(POINT sp, POINT ep, POINT op)
{
    return((sp.x - op.x)*(ep.y - op.y) - (ep.x - op.x)*(sp.y - op.y));
}

bool InsideConvexPolygon(int vcount, POINT polygon[], POINT q) // 可用於三角形！ 
{
    POINT p;
    LINESEG l;
    int i;
    p.x = 0; p.y = 0;
    for (i = 0; i<vcount; i++) // 尋找一個肯定在多邊形polygon內的點p：多邊形頂點平均值 
    {
        p.x += polygon[i].x;
        p.y += polygon[i].y;
    }
    p.x /= vcount;
    p.y /= vcount;

    for (i = 0; i<vcount; i++)
    {
        l.s = polygon[i]; l.e = polygon[(i + 1) % vcount];
        if (multiply(p, l.e, l.s)*multiply(q, l.e, l.s)<0) /* 點p和點q在邊l的兩側，說明點q肯定在多邊形外 */
            break;
    }
    return (i == vcount);
}

void find(int x, int y, int &X, int &Y)
{
    double ox, oy;
    POINT pp[6];
    for (int i = -9; i <= 10; i++)
        for (int j = -9; j <= 10; j++)
        {
            oy = 7.5*j;
            ox = 5 * sqrt(3)*i + j*2.5*sqrt(3);
            pp[0].x = ox;
            pp[0].y = oy + 5;
            pp[1].x = ox + 2.5*sqrt(3);
            pp[1].y = oy + 2.5;
            pp[2].x = ox + 2.5*sqrt(3);
            pp[2].y = oy - 2.5;
            pp[3].x = ox;
            pp[3].y = oy - 5;
            pp[4].x = ox - 2.5*sqrt(3);
            pp[4].y = oy + 2.5;
            pp[5].x = ox - 2.5*sqrt(3);
            pp[5].y = oy - 2.5;
            if (InsideConvexPolygon(6, pp, POINT(x, y)))
            {
                X = i;
                Y = j;
                return;
            }
        }
}

int main()
{
    int x, y;
    int X, Y;
    scanf("%d%d", &x, &y);
    find(x, y, X, Y);
    printf("[%d,%d]", X, Y);
    for (int i = 2; i <= 10; i++)
    {
        scanf("%d%d", &x, &y);
        find(x, y, X, Y);
        printf(", [%d,%d]", X, Y);
    }
    printf("\n");
}

J.Minimun Distance in a Star Graph（貪心思想）
題目連結：https://nanti.jisuanke.com/t/17317
題意：他囉裡八嗦講了一大堆。其實就是從a狀態變成b狀態。
每次只能把第一個數和另一個數交換。求最小的交換次數，從a變到b。
POINT：貪心思想。把b序列變成12345n，把a序列對印b起來。
若第一個數不是1，則把它歸位，交換他們 ans++。
若是1，則把1和後面錯誤的數交換，ans++。
這樣交換下去便是最小的交換次數，輸出ans。
主要還是讀懂題目。
下面給出程式碼：

#include <bits/stdc++.h> 
using namespace std;  
int n,ans[10],mean[15];  
int num[15];  
int work()  
{  
    int ans=0;  
    while(1)  
    {  
        if(num[1]!=1)  
        {  
            ans++;  
            swap(num[1],num[num[1]]);  
        }  
        else  
        {  
            int flag=0;  
            for(int i=1;i<=n;i++)  
            {  
                if(num[i]!=i)  
                {  
                    flag=1;  
                    ans++;  
                    swap(num[1],num[i]);  
                    break;  
                }  
            }  
            if(!flag) break;  

        }  
    }  
    return ans;  
}  
int main()  
{  
    while(scanf("%d",&n)!=EOF)  
    {  
        memset(mean,0,sizeof mean);  
        for(int i=1;i<=5;i++)  
        {  
            char s1[15],s2[15];  

            scanf("%s%s",s1,s2);  
            for(int i=0;i<n;i++)  
            {  
                mean[s2[i]-'0'] = i+1;  
            }  
            for(int i=0;i<n;i++)  
                num[i+1] = mean[s1[i]-'0'];  
            printf("%d\n",work());  
        }  
    }  
    return 0;  
}

K.Line Segments Clipped by Windows
題目連結：https://nanti.jisuanke.com/t/17318
本題暫時還沒有找到AC程式碼，待補
L.The Heaviest Non-decreasing Subsequence Problem（LIS,最長不遞減子序列）
題目連結：https://nanti.jisuanke.com/t/17319
PS：這是我們最後死磕的一道題，2小時還沒A，感覺心態真的爆炸，一上手看到這題就說是LIS，然後套模板，感覺不對又重新看了一邊題目，發現還是LIS沒變，模板改了20+，交上去不是WA就是CE，賽後問了才知道是要拆開解決，暈了。
題意：最長上升子序列。但是每個數的權值不一樣，有的是1，有的是0，有的是5。求最大權值的最長上升子序列。
POINT：把權值為0的去掉，把權值為5的複製5個放進陣列。
再跑一遍nlogn的最長上升子序列，就是答案。
下面給出程式碼：

#include<bits/stdc++.h> 
using namespace std;  
#define LL long long  
const LL maxn = 1e6+888;  
int n=0;  
int num[maxn];  
int a[maxn];  
int main()  
{  
    int q;  
    while(~scanf("%d",&q))  
    {  
        int flag=0;  
        if(q>=10000)  
        {  
            q=q-10000;  
            flag=1;  
        }  
        if(q<0) continue;  
        if(flag)  
        {  
            for(int i=1;i<=5;i++)  
            {  
                num[++n]=q;  
            }  
        }  
        else  
            num[++n]=q;  
    }  
    if(n==0)  
    {  
        printf("0\n");  
        return 0;  
    }  
    int now=1;  
    a[1]=num[1];  
    for(int i=2;i<=n;i++)  
    {  
        if(num[i]>=a[now]) a[++now]=num[i];  
        else  
        {  
            int l=upper_bound(a+1,a+1+now,num[i])-a;  
            a[l]=num[i];  
        }  
    }  
    printf("%d\n",now);  
}

M.Frequent Subsets Problem（進位制運算或者集合）
題目連結：https://nanti.jisuanke.com/t/17320
PS：看到這題，本來想說怎麼感覺有點複雜，看來還是英文沒讀懂，暈，賽後一問，進位制運算/集合，整個人都不好了，突然想打人。MMP
題意：
給你一個n和a。n代表資料裡只有1-n值的數字。
給你m個集合，讓你求出存在幾個子集，他在這m個集合裡出現的次數>=a*m。
我們先來看一下進位制運算的想法。
因為n只到20,直接利用二進位制的位運算暴力解決,1代表有該元素,0代表沒有該元素
給出程式碼：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;


int n;
double m;
stringstream ss;
string s;
int t;
int c[55];
int sum=0;
int main()
{
//    freopen("data.txt","r",stdin);
    ios_base::sync_with_stdio(false);
    memset(c,0,sizeof(c));
    getline(cin,s);
    ss<<s;
    ss>>n>>m;
    while(getline(cin,s))
    {
        ss.clear();
        ss<<s;
        while(ss >> t)
        {
            c[sum] |= ( 1<<(t-1) );
        }
//        cout <<c[sum]<<endl;
        sum++;
    }
    int xx = ceil(m*sum);
    int ans = 0;
    int maxx = (1<<n);
    for(int i=1;i<=maxx;i++)
    {
        int ct = 0;
        for(int j=0;j<sum;j++)
        {
            if((i&c[j])==i)
            {
//                cout <<(i&c[j])<<" "<<i<<endl;
                ct++;
            }
        }
//        if(ct)cout<<ct<<endl;
        if(ct>=xx) ans++;
    }
    cout<<ans<<endl;
    return 0;
}

下面我們來看一下集合思想的做法：
一個一個找，找1，1如果可以作為答案，找1 2。1 2不行找1 3。1 2行就找1 2 3。
接著找2，2可以找2 3，2 3不行找2 4。
這樣需要剪枝，找1的時候肯定只存在在某幾個集合中，做一個標記，繼續找下去只要在這幾個集合中找就行了。再繼續更新標記，範圍會越來越少
給出程式碼：

#include<bits/stdc++.h>
using namespace std;
int flag[55][22];
int ans;
int num,temp,n;
void work(int x,int aim[])
{
    int nn=0;
    int faim[55];
    for(int i=1;i<=num;i++)
        faim[i]=aim[i];
    for(int i=1;i<=num;i++)
    {

        if(flag[i][x]&&faim[i])
        {
            faim[i]=1;
            nn++;
        }
        else
            faim[i]=0;
    }
    if(nn>=temp)
    {
        ans++;
        for(int i=x+1;i<=n;i++)
        {
            work(i,faim);
        }
    }
}
int main()
{
    double a;
    scanf("%d %lf",&n,&a);
    int d;
    num=1;
    while(~scanf("%d",&d))
    {
        char c;
        scanf("%c",&c);
        flag[num][d]=1;
        if(c=='\n')
            num++;
    }
    num--;
    temp=ceil((double)num*a);
    ans=0;
    for(int i=1;i<=n;i++)
    {
        int aim[55];
        for(int i=1;i<=num;i++) aim[i]=1;
        work(i,aim);
    }
    printf("%d\n",ans);
    return 0;
}

以上就是ACM-ICPC2017年南寧網路賽的題目及其題解收集了，有些題目由於還沒有找到題解，所以還是待補狀態，等有大佬放在網上之後再進行編輯。感謝網上給出AC程式碼的大佬們。
今年的ACM網路賽估計沒了，上海的EC不知道是不是沒有網路賽，如果沒有，那南寧是今年ACM網路賽的最後一場了。我們2018ACM見

相關推薦

ACM-ICPC 2017南寧賽區網路賽題目題解收集

前言：本篇文章的主要程式碼來自於CSDN部落格或者網路，感謝網路ACMdalao的AC程式碼，佩服他們，本文最後會寫出各個AC程式碼的原作者和網址。（注意一點，每個程式的標頭檔案我都改成了萬能標頭檔案，測試時間可能會加長，如果需要原始碼的標頭檔案請直接在程式碼後

計蒜客-2017 ACM-ICPC 亞洲區(烏魯木齊賽區)網路賽J題Our Journey of Dalian Ends (最小費用最大流)

題意： 給定若干個城市，出發點為大連，目的地為西安，但是要求中途必須經過上海，並且圖中每個城市只能經過一次，給出m條路(雙向道路)，走第i條路需要wi代價，求所有滿足要求的方案中花費的最小代價，如果沒有滿足的方案，輸出-1。 思路： 相當於求從大連到上海加上西安到上海花費的

HDU6201 | 2017 ACM-ICPC 亞洲區(瀋陽賽區)網路賽-H transaction transaction transaction

題意：一個n個點n-1條邊的無向圖，每個點每條邊都有權值，求一條路徑W終點-W路徑-W起點的最大值； 思路：dp，dp[i]表示以i為終點的路徑的最大值，若x於y相連，那麼有dp[x]=max(dp[

6197 array array array (2017 ACM-ICPC 亞洲區 (瀋陽賽區) 網路賽 1004)

array array array Problem Description One day, Kaitou Kiddo had stolen a priceless diamond ring. But detective Conan blocked Kiddo's

2017 ACM-ICPC 亞洲區(西安賽區)網路賽 E Maximum Flow

題目連結 題意 有 n 個點，0,1,2,...,n−1，對於沒對點 <i,j>(0≤i<j<n)，有一條 i→j 邊，流量為 iXorj，問從 0 到 n−1 的最大流

ACM-ICPC 2018南京賽區網路賽 I.Skr （迴文自動機）

計蒜客開了禁止複製，我掛了破解網頁限制的指令碼能複製但是不太好看，就不貼題目了。 題目大意是給出一個數字串，求其本質不同的迴文子串的和。 一開始沒看到“本質不同”，上來就想跑馬拉車 + Sam，

ACM-ICPC 2018 焦作賽區網路賽 H. String and Times（字尾自動機）

下午打的網路賽，一上來就開了這題，打算秒，結果發現題面沒有給字串長度，最後還是出題人在提問區補的，真的想打人。 字尾自動機裸題，大概就是以下這兩題合在一起： hihocoder上都有題解。 很裸，求一下endpos，再根據自動機性質，用maxl

ACM-ICPC 2018 徐州賽區網路賽

學長們還是太強了，膜拜，雖然和清華北大那些比不了，但是還是比較強的，畢竟他們只有三個人，寫了7題 下面是學長們的程式碼 A題 After Incident, a feast is usually held in Hakurei Shrine. This time

ACM-ICPC 2018 徐州賽區網路賽 F. Features Track(雜湊+暴力)

Morgana is learning computer vision, and he likes cats, too. One day he wants to find the cat movement from a cat video. To do this, he ex

ACM-ICPC 2018 焦作賽區網路賽

B. Mathematical Curse （DP） 這是一類題目，DP求最大最小值，因為存在正負值反轉所以最大值最小值都要儲存。 #pragma GCC optimize(2) #pragma GCC optimize(3) #include <bits

ACM-ICPC 2018 南京賽區網路預賽部分題解

5題順利進現場 A 簽到 思路：打表找規律即可 L 最短路 隊友秒過，聽說是BZOJ原題，改為有向圖 J 線性篩 / 分塊打表 ,ans=f(n)的字首和 線性篩：

ACM-ICPC 2018 徐州賽區網路預賽部分題解

5題進不去現場 I.水模擬，隊友秒過 題意：給一個長度為n的字串s，再給一個字元c，將字串每一個字元的ASCII碼-c的ASCII碼，保留前導零，使得數字為兩位，然後去掉整串數字的前導零，輸出數

2018ACM-ICPC焦作賽區網路賽題目---Give Candies

                                                  Give Candies 時間限制： 1000ms         記憶體限制： 65536K There are N children in kindergarten. M

2017 烏魯木齊賽區網路賽 Coconut（【模擬題目】）

題目連結：https://nanti.jisuanke.com/t/16952 【中文題意】有一個闊愛的小動物從1點出發，他要去n點，在旅途中，他每天要吃m個糖果，不然他就會GG，在第i個城市他可以獲

ACM-ICPC 2016 大連賽區現場賽 K. Guess the number && HDU 5981

題意 clu 題解 php art min ble freopen tps 題目鏈接：http://acm.hdu.edu.cn/showproblem.php?pid=5981 題意：A在[L, R]之間隨機選取一個數X，之後B來猜這個數，如果猜的數比X小，那麽A就告訴B

ACM-ICPC 2018 瀋陽賽區網路預賽 J. Ka Chang （分塊+樹狀陣列+dfs序）

題意 給你一顆樹，由兩種操作： 1.把這棵樹深度為 D D D的點全部都加上一個值。 2.求以p為根節點的子樹的權值和是多少？ 思路 對於樹上的東西，我們可以把他求一下DFS序，之後就可以把樹上的結構變成

ACM-ICPC 2018 徐州賽區網路預賽 H. Ryuji doesn't want to study （線段樹維護字首和的字首和）

題意 很簡答就是每次查詢 (L,R)的時候 ，查詢 a[L]∗(R−L+1)+a[L+1]∗(R−L−1)+a[L+2]∗(R−L−2)....a[R]∗1 a [

ACM-ICPC 2018 徐州賽區網路預賽 G. Trace (線段樹維護)

題意 你在海灘上有浪花，所有的浪花都是矩形的，當一個浪花來了之後，就會覆蓋他的前一個浪花，問你最後浪花的周長和 思路 我們從後往前來，這樣的話，我們處理的都是會留下來的，怎樣的會留下來呢？ 首先我們先看1號點和2號點，由圖我們可以很明顯的看出1號點會被淹沒，而1`和1“他們不會被淹沒

ACM-ICPC 2018 徐州賽區網路預賽 B. BE, GE or NE (記憶化搜尋)

題意 兩個人在玩遊戲，有一個初始的分數，每次輪流玩遊戲有三種操作，當前數字加上A，當前數字減去B，當前數字乘上-1，當最終分數>h 的時候就是good ending，小於l的時候就是bad ending ，其他的都是 Normal Ending。 思路 從第一次操作開始記憶化搜，

ACM-ICPC 2018 南京賽區網路預賽 J AC Challenge (狀壓dp)

題意 給你n道題，在你做第 i i {i}道題的時候有 p[j] p