題目大意

有n個結點的一棵樹，每條邊有兩個權值a,b，第t天經過第i條邊花費時間ait+b$a_{i}t+b$，給定m，求t=0,1,2...m−1$t=0,1,\mathrm{2...}m-1$時，最長的路徑長度。

題解

簡介邊分治

類似點分治選擇重心，邊分治選擇一條邊，把樹分成兩邊，使得兩邊的點數最接近。
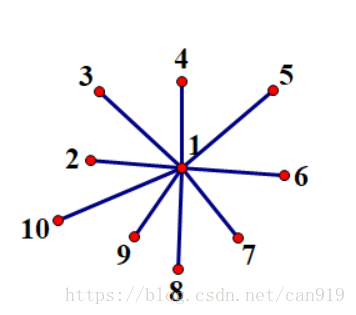
但對普通的樹進行邊分治容易退化，如下面這種圖會退化為O(n)$O(n)$（官方題解稱為star tree）

所以使用邊分治，需要將一般樹，轉化為二叉樹，這樣邊分治分成的兩塊，保證了兩塊的節點數一定在[n3,n2]$[\frac{n}{3},\frac{n}{2}]$之間。

邊分治相對於點分治的優點在於，它只會把樹分成兩塊，在有些情況下，合併結果時，減少大量程式碼量。

本題的邊分治

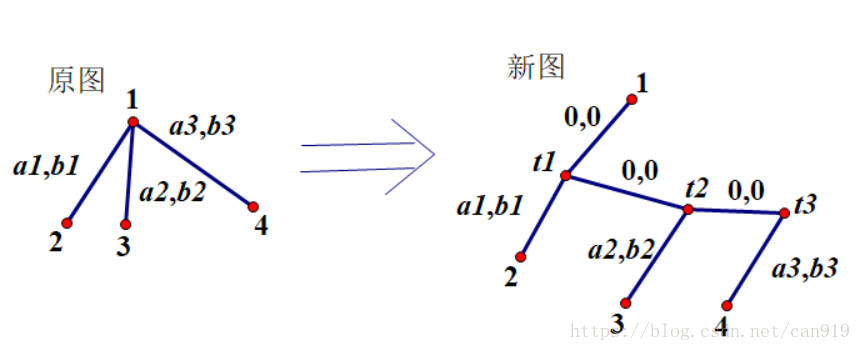
在多叉樹轉二叉樹時，對於本題，我們必須保證任意兩點的距離不變，轉二叉時需要新建節點，如下圖：

對於邊分治的一棵數，計算每個子樹的大小siz[u]，找到最大的子樹並且大小 < 總大小的一半，選擇這個結點和它父親結點的邊作為重心邊，分成兩棵樹。

對於分成的兩棵樹
易知，最長路經一定是從根走到葉子節點的路徑，統計所有路徑，把a值和b值分別加起來，得到這條路徑的函式at+b$at+b$。

這兩棵樹，我們都可以得到一大堆路徑的函式，合併兩個路徑即分別相加他們的a值和b值，現在考慮如何O(n)$O(n)$合併所有路徑。
設ai<aj$a_i<a_j$

對於每個函式at+b$at+b$，將其看作一個點(a,b)$(a,b)$，根據斜率式，將維護上凸包，斜率遞減（不懂可見斜率優化）

將分成的兩棵樹分別得到的所有路徑函式，分別建立兩個凸包。
合併時，用兩個變數x,y，表示當前合併到這兩個凸包的第幾個結點，每次判斷x與x+1的斜率k1，y與y+1的斜率k2，選擇斜率更大的+1，再將新的x結點與y結點合併（選擇斜率大的合併，保證了在新凸包中斜率變化量更小，才能使凸包中結點不漏選）

做完邊分治，我們得到了整棵樹所有有用路徑的函式凸包，已經保證了答案的單調，直接計算即可。

程式碼

#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXN=200005,MAXM=MAXN*3;

struct Edge
{
    int v,a,b,id;
    Edge()=default;
    Edge(int _v,int _a,int _b,int _id):v(_v),a(_a),b(_b),id(_id) {}
};

class Tree
{
public:
    int n;
    vector<Edge> adj[MAXN*2];

    vector<Edge> &operator [] (unsigned int i)
    {
        return adj[i];
    }
    void AddEdge(int u,int v,int a,int b,int i)
    {
        adj[u].emplace_back(v,a,b,i);
        adj[v].emplace_back(u,a,b,i);
    }
};

struct Path
{
    long long a,b;
    Path()=default;
    Path(long long _a,long long _b):a(_a),b(_b) {}
    bool operator < (const Path &t)const
    {
        return a<t.a||(a==t.a&&b<t.b);
    }
};

int N,M,edgeid;
Tree F,G;

void ToBinaryTree(int u,int fa=0)
{
    int last=u;
    for(const auto &e:F[u])
        if(e.v!=fa)
        {
            G.AddEdge(last,++G.n,0,0,++edgeid);//fprintf(stderr,"[%d->%d: 0,0]\n",last,G.n);
            G.AddEdge(G.n,e.v,e.a,e.b,++edgeid);//fprintf(stderr,"[%d->%d: %d,%d]\n",G.n,e.v,e.a,e.b);
            last=G.n;
            ToBinaryTree(e.v,u);
        }
}

bool disable[MAXM];
int siz[MAXN];
Edge E[MAXN];
void GetSize(int u,int fa=0)
{
    siz[u]=1;
    for(const auto &e:G[u])
        if(e.v!=fa&&!disable[e.id])
        {
            E[e.v]=Edge(u,e.a,e.b,e.id);
            GetSize(e.v,u);
            siz[u]+=siz[e.v];
        }
}
int FindCentroid(int u,int lim,int fa=0)
{
    if(siz[u]<=lim)
        return u;
    int mxsiz=0,id;
    for(const auto &e:G[u])
        if(e.v!=fa&&!disable[e.id])
        {
            int tmp=FindCentroid(e.v,lim,u);
            if(siz[tmp]>mxsiz)
                mxsiz=siz[tmp],id=tmp;
        }
    return id;
}

void GetPath(int u,vector<Path> &P,Path now=Path(0,0),int fa=0)
{
    if(G[u].size()==1)
        P.push_back(now);
    for(const auto &e:G[u])
        if(e.v!=fa&&!disable[e.id])
            GetPath(e.v,P,Path(now.a+e.a,now.b+e.b),u);
}

void Process(vector<Path> &P)
{
    static vector<Path> tmp;
    sort(P.begin(),P.end());
    tmp.resize(P.size());
    tmp.emplace_back(0,0);
    int top=0;
    for(const auto &p:P)
    {
        while(top>0&&(p.a==tmp[top].a&&p.b>=tmp[top].b))
              top--;
        if(p.a==tmp[top].a&&p.b<=tmp[top].b)
            continue;
        while(top>0&&1.0*(tmp[top].b-tmp[top-1].b)/(tmp[top].a-tmp[top-1].a)<1.0*(p.b-tmp[top].b)/(p.a-tmp[top].a))
            top--;
        tmp[++top]=p;
    }
    for(int i=0; i<=top; i++)
        P[i]=tmp[i];
    P.resize(top+1);
}

vector<Path> P1,P2,P;

void CentroidDecomposition(int u)
{
    GetSize(u);
    if(siz[u]<=1)
        return;
    int centroid1=FindCentroid(u,siz[u]/2);
    int centroid2=E[centroid1].v;

    disable[E[centroid1].id]=true;
    P1.clear();
    P2.clear();
    P1.emplace_back(0,0);
    P2.emplace_back(0,0);
    GetPath(centroid1,P1);
    GetPath(centroid2,P2);

    Process(P1);
    Process(P2);

    int x=0,y=0;
    while(x<(int)P1.size()&&y<(int)P2.size())
    {
        P.emplace_back(P1[x].a+P2[y].a+E[centroid1].a,P1[x].b+P2[y].b+E[centroid1].b);
        double k1=-1e100,k2=-1e100;
        if(x<(int)P1.size()-1)
            k1=1.0*(P1[x+1].b-P1[x].b)/(P1[x+1].a-P1[x].a);
        if(y<(int)P2.size()-1)
            k2=1.0*(P2[y+1].b-P2[y].b)/(P2[y+1].a-P2[y].a);
        if(k1>k2)
            x++;
        else
            y++;
    }

    CentroidDecomposition(centroid1);
    CentroidDecomposition(centroid2);
}

int main()
{
    scanf("%d%d",&N,&M);
    F.n=N;
    for(int i=1; i<N; i++)
    {
        int u,v,a,b;
        scanf("%d%d%d%d",&u,&v,&a,&b);
        F.AddEdge(u,v,a,b,i);
    }

    G.n=N;
    ToBinaryTree(1);

    P.emplace_back(0,0);
    CentroidDecomposition(1);
    Process(P);

    int id=0;
    for(int t=0; t<M; t++)
    {
        while(id<(int)P.size()-1&&(1LL*t*P[id+1].a+P[id+1].b)>(1LL*t*P[id].a+P[id].b))
            id++;
        long long ans=1LL*t*P[id].a+P[id].b;
        printf("%I64d ",ans);
    }
    puts("");

    return 0;
}