滿足以下兩個條件的樹形結構叫做二叉樹

1.每個結點的度都不大於2
2.每個結點的孩子次序不能顛倒

性質

• 在二叉樹的第i層上至多有2^(i-1)個結點
• 深度為k的二叉樹上至多有2^k-1個結點
• 對任何一棵二叉樹，若它含有n0 個葉子結點、n2 個度為 2 的結點，則必存在關係式：n0 = n2+1。
• 具有n個結點的完全二叉樹的深度為log2n +1。
• 如果對一棵有n個結點的完全二叉樹的結點按層序編號,則對任一結點i（1<=i<=n),有：
  （1）如果i＝1，則結點i無雙親，是二叉樹的根；如果i>1，則其雙親的編號是
  i/2(整除）。
  （2）如果2i>n，無左孩子；否則，其左孩子是結點2i。
  （3）如果2i＋1>n，則結點i無右孩子；否則，其右孩子是結點2i＋1。

滿二叉樹與完全二叉樹的概念

• 滿二叉樹：深度為k且有個2^k-1結點的二叉樹。
• 完全二叉樹：深度為k，節點數為n的二叉樹，如果其結點1~n的位置序號分別與滿二叉樹的結點1~n的位置序號一一對應，則為完全二叉樹。其中，度為1的結點數目要麼為1，要麼為0

常見題目

• 已知完全二叉樹第6層上有10個葉子結點，則這棵二叉樹的結點總數最多是 ？個
  最多：第六層滿,前六層共有2^6-1=63個，第七層有：2*(2^(6-1)-10)=44，共有107個。
  最少：第六層只有10個，前五層滿共有2^5-1=31個，則共有41個結點。

• 一棵具有n個結點的二叉樹，若它有m個葉子結點，則該二叉樹中度為1的結點個數是 ？

  
  度為2的結點個數：m-1,則度為1的結點個數為：n-m-(m-1)，即n-2m+1

• 已知二叉樹中有30個葉子結點，則二叉樹的總結點個數至少是 ？
  30（度為0）+29（度為2）+0（度為1） = 59

• 一棵深度為6的滿二叉樹有 ？ 個分支結點和 ？ 個葉子
  分支結點即度為1和度為2的結點
  n0 = 2^(6-1) = 2^5 = 32
  滿二叉樹中，n0 = 0, n2 = n0 - 1 = 31
  所以分支結點數目為 n1+n2=0+31=31,葉子結點數=32

• 含有11個結點的不相似的二叉樹有 ? 棵
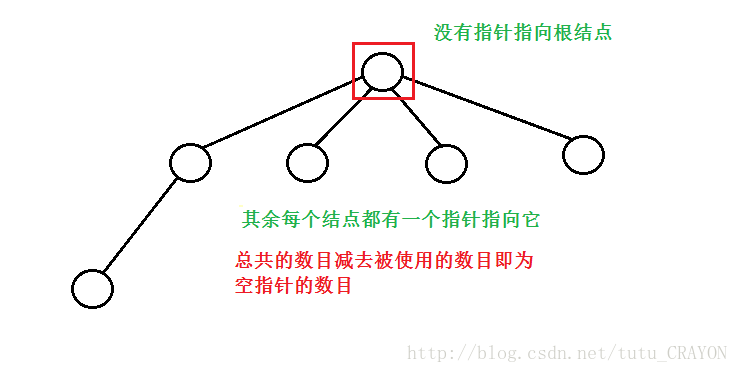
  含n個結點的不相似的二叉樹有[C(2n,n)]/(n+1)棵,即[ 22! / ( 11!*11!) ] / 12 = 58786 種 （卡特蘭數的概念）

• 一個包含n個結點的四叉樹，每個結點都有4個指向孩子結點的指標，這4個指標中有 ？ 個空指標
  共有4n個指標，其中僅有n-1個指標被使用，因為沒有指標指向根結點，其餘結點都有一個指標指向它，所以共有4n-(n-1)=3n-1個指標。