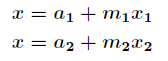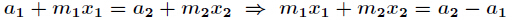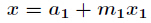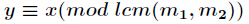題意：

給的模數不滿足互質，求同餘方程組的解

思路：

同樣是求這個東西。。
X mod m1=r1
X mod m2=r2
...
...
...
X mod mn=rn

首先，我們看兩個式子的情況
X mod m1=r1……………………………………………………………(1)
X mod m2=r2……………………………………………………………(2)
則有 
X=m1*k1+r1………………………………………………………………(*)
X=m2*k2+r2
那麼 m1*k1+r1=m2*k2+r2
整理，得
m1*k1-m2*k2=r2-r1
令(a,b,x,y,m)=(m1,m2,k1,k2,r2-r1)，原式變成
ax+by=m
熟悉吧？

此時，因為GCD(a,b)=1不一定成立，GCD(a,b) | m 也就不一定成立。所以應該先判 若 GCD(a,b) | m 不成立，則！！！方程無解！！！。
否則，繼續往下。

解出(x,y)，將k1=x反代回（*），得到X。
於是X就是這兩個方程的一個特解，通解就是 X'=X+k*LCM(m1,m2)
這個式子再一變形，得 X' mod LCM(m1,m2)=X
這個方程一出來，說明我們實現了(1)(2)兩個方程的合併。
令 M=LCM(m1,m2)，R=r2-r1
就可將合併後的方程記為 X mod M = R。

然後，擴充套件到n個方程。
用合併後的方程再來和其他的方程按這樣的方式進行合併，最後就能只剩下一個方程 X mod M=R，其中 M=LCM(m1,m2,...,mn)。
那麼，X便是原模線性方程組的一個特解，通解為 X'=X+k*M。

如果，要得到X的最小正整數解，就還是原來那個方法：

X%=M;
if (X<0) X+=M;

程式碼一：

//不滿足模數兩兩互質
#include <iostream>  
#include <string.h>  
#include <stdio.h>  
#define ll __int64
using namespace std;

const int inf = 0x3f3f3f3f;
const int maxn = 1e5 + 5;
int n;
ll m[maxn], r[maxn];

void extgcd(ll a, ll b, ll &d, ll &x, ll &y){
  if (!b) {d = a, x = 1, y = 0;}
  else{
    extgcd(b, a % b, d, y, x);
    y -= x * (a / b);
  }
}

ll extcrt(ll *m, ll *r, int n){
  ll M = m[1], R = r[1], x, y, d;
  for (int i = 2; i <= n; ++i){
    extgcd(M, m[i], d, x, y);
    if ((r[i] - R) % d) return -1;
    x = (r[i] - R) / d * x % (m[i] / d);
    R += x * M;
    M = M / d * m[i];
    R %= M;
  }
  return R > 0 ? R : R + M;
}

int main(){
  while (~scanf("%d",&n)){
    for (int i = 1; i <= n; ++i)
      scanf("%I64d%I64d", &m[i], &r[i]);
    printf("%I64d\n",extcrt(m,r,n));
  }
    return 0;
}
 

普通的中國剩餘定理要求所有的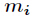互素，那麼如果不互素呢，怎麼求解同餘方程組？

這種情況就採用兩兩合併的思想，假設要合併如下兩個方程

那麼得到

在利用擴充套件歐幾里得演算法解出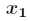的最小正整數解，再帶入

得到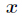後合併為一個方程的結果為

這樣一直合併下去，最終可以求得同餘方程組的解。

#include <iostream>  
#include <string.h>  
#include <stdio.h>  
#define ll __int64
#define rep(i,k,n) for(int i=k;i<=n;i++)
using  namespace  std;

const int N=1010;
ll a[N],m[N];

ll gcd(ll a,ll b){
  return b ? gcd(b, a%b) : a;
}

void extgcd(ll a, ll b, ll &x, ll &y)  {  
  if(b == 0){  
    x = 1; y = 0;  
    return;  
  }  
  extgcd(b, a % b, x, y);  
  ll tmp = x;  
  x = y;  
  y = tmp - (a / b) * y;  
}  
  
ll inv(ll a,ll m){//a模m的逆元
  ll x, y;  
  extgcd(a, m, x, y);//a*x+m*(-k)=1
  return (x % m + m) % m;
}  

bool merge(ll a1, ll m1, ll a2, ll m2, ll &a3, ll &m3){
  ll d = gcd(m1, m2);  
  ll c = a2 - a1;  
  if(c % d) return false;  
  c = (c % m2 + m2) % m2;  
  m1 /= d;  
  m2 /= d;  
  c /= d;  
  c *= inv(m1, m2);  
  c %= m2;  
  c *= m1 * d;  
  c += a1;  
  m3 = m1 * m2 * d;  
  a3 = (c % m3 + m3) % m3;  
  return true;  
}
  
ll CRT(ll a[],ll m[],int n){
  ll a1=a[1],m1=m[1];
  rep(i, 2, n){  
    ll a2=a[i], m2=m[i];  
    ll a3, m3;
    if(!merge(a1, m1, a2, m2, a3, m3))
      return -1;
    a1 = a3, m1 = m3;
  }  
  return (a1 % m1 + m1) % m1;  
} 

int main(){
  int n;
	while(~scanf("%d",&n)){
		rep(i, 1, n)scanf("%I64d%I64d",&m[i], &a[i]);
    ll ans=CRT(a, m, n);
    printf("%I64d\n", ans);
	}
	return 0;
}