二分搜尋樹設計思想及實現
二分搜尋樹
定義
二分搜尋樹(Binary Search Tree),也稱二叉查詢樹,有序二叉樹,排序二叉樹,是指一棵空樹或者具有下列性質的二叉樹:
- 若任意節點的左子樹不空,則左子樹上所有結點的值均小於它的根結點的值;
- 任意節點的右子樹不空,則右子樹上所有結點的值均大於它的根結點的值;
- 任意節點的左、右子樹也分別為二叉查詢樹。
沒有鍵值相等的節點(no duplicate nodes)。
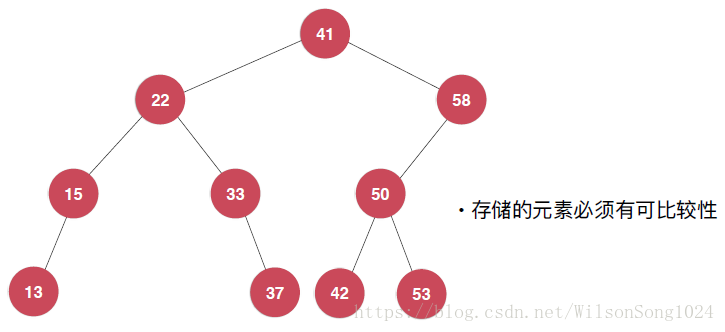
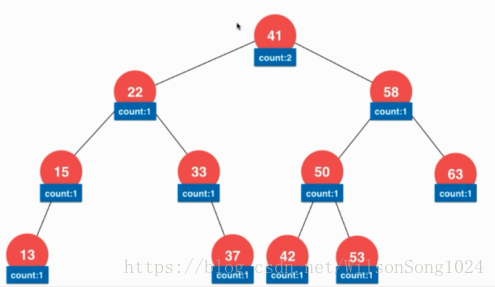
如下圖就是一個二分搜尋樹,其本質就是一個二叉樹,並且不一定是滿的,而且元素要可比較大小。
優勢
二分搜尋樹在某些方面是具有優勢的,比如我們從時間複雜度上來分析一下:
實現
二分搜尋樹的實現
簡單的實現一下,通過一個私有類實現包含其所需的節點,值,左節點,右節點。
public class BinarySearchTree<E extends Comparable<E>> {
/**
* 定義樹節點的私有類
* @param <E>
*/
private class Node{
public E e;
public Node left, right;
public Node(E e){
this.e = e;
left = null 向樹中新增元素
其實插入元素使用遞迴的方式很容易,其核心思想:從根節點開始找插入的位置,滿足二叉搜尋樹的特性,比左子節點大,比右子節點小.
具體的步驟:
從根節點開始,先比較當前節點,如果當前節點為null那麼很明顯就應該插入到這個節點。
如果上面的節點不是null,那麼和當前節點比較,如果小於節點就往左子樹放,如果大於節點就往右子樹放。
然後分別對左子樹或者右子樹遞迴的遞迴進行如上1、2步驟的操作
此時就用到了遞迴,那麼遞迴是對某一個問題,它的子問題需要是同樣的模型。此處的一個小的問題就是:對某個node,然後進行操作,所以引數應該有個node才能實現迴圈起來。此處向以node為根的二叉搜尋樹中,插入節點value.
/**
* 新增元素
* @param e 新增的元素
*/
public void add(E e){
root = add(root, e);
}
/**
* 遞迴的新增元素
* 向以node為根的二分搜尋樹中插入元素e,遞迴演算法
* 返回插入新節點後二分搜尋樹的根
* @param node 樹節點
* @param e 元素
* @return
*/
private Node add(Node node, E e){
if (node == null){
size ++;
return new Node(e);
}
if (e.compareTo(node.e) > 0){
node.right = add(node.right, e);
}
if (e.compareTo(node.e) < 0){
node.left= add(node.left, e);
}
return node;
}
注意
在這裡摳一下關於遞迴新增元素這個函式為啥要返回插入新節點後二分搜尋樹的根,
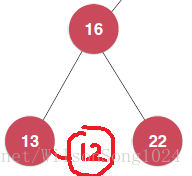
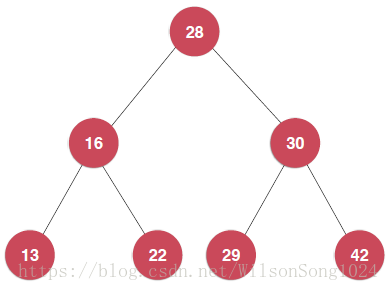
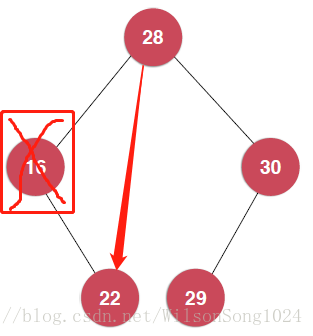
比方說上面這棵樹,我要新增元素12,執行遞迴的第一步之後,node節點其實是28這個根節點,然後執行
add(node.left, e);
其實就是像下面的樹中新增元素,但是現在的節點還是28,執行完之後就是下面這棵樹,返回以16為根節點的這棵樹,然後賦值給node.left。其實就是相當於把這棵樹連線到了28這個節點上。最後返回node也就是28這個節點,其實就是新新增元素之後的樹。
查詢樹中包含某一個元素
其實查詢包含樹中是否包含某個元素與向樹中新增一個元素的思路是類似的,都是通過遞迴的方式查詢左右子樹。
/**
* 查詢是否包含元素
* @param e 元素
* @return
*/
public boolean contain(E e){
return contains(root, e);
}
/**
* 遞迴的查詢是否包含某個元素
* @param node 樹節點
* @param e 元素
* @return
*/
private boolean contains(Node node, E e){
if (node == null){
return false;
}
if (e.compareTo(node.e) < 0){
return contains(node.left, e);
}else if (e.compareTo(node.e) > 0){
return contains(node.right, e);
}else {
return true;
}
}樹的遍歷
其實樹的遍歷和圖的遍歷是一樣的,分為兩種,一種是廣度優先遍歷,一種是深度優先遍歷。
深度優先遍歷
深度優先遍歷又分為三種:
前序遍歷(Preorder Traversal):先訪問當前節點,再依次遞迴訪問左右子樹
中序遍歷(Inorder Traversal):先遞迴訪問左子樹,再訪問自身,再遞迴訪問右子樹
後序遍歷(Postorder Traversal):先遞迴訪問左右子樹,最後再訪問當前節點。
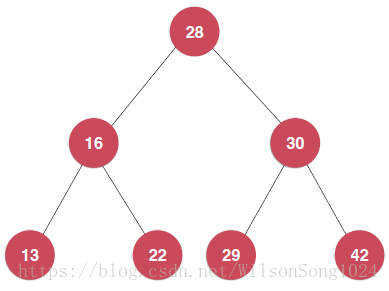
比如一棵樹:
前序遍歷的結果是:28–16–13–22–30–29–42
中序遍歷的結果是:13–16–22–28–30–29–42
後序遍歷的結果是:13–22–16–29–42–30–28
前序遍歷的遞迴實現
遞迴實現的思想是非常簡單的,從根節點開始,判斷根節點是否有值,有則輸出,然後遞迴的去處理器左子樹,最後去處理其右子樹。
/**
* 前序遍歷
*/
public void preOrder(){
preOrder(root);
}
/**
* 遞迴前序遍歷
* @param node
*/
public void preOrder(Node node){
if (node == null){
return;
}else {
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
}前序遍歷的非遞迴實現
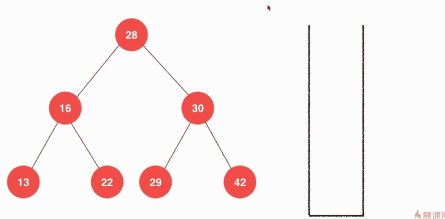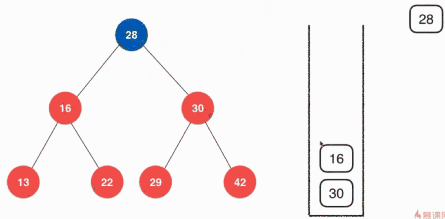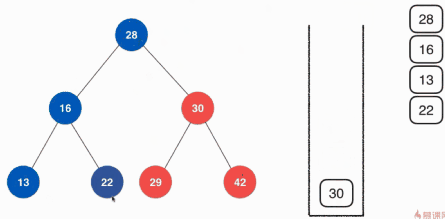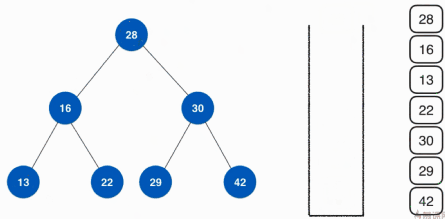
關於前序遍歷的非遞迴實現這裡使用棧的方式,具體的思路如下:
具體的實現其實就是從根節點開始向堆疊中壓入元素,然後彈出元素,然將該根節點的左右孩子按順序壓入堆疊,然後彈出棧頂元素,在將彈出的元素的左右孩子按順序壓入堆疊,不斷的執行,直到樹中沒有元素,堆疊中就只彈出元素,直至堆疊為空。
具體的實現如下:
/**
* 非遞迴的實現二分搜尋樹的前序遍歷
*/
public void preOrderNR(){
Stack<Node> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null){
stack.push(cur.right);
}
if (cur.left != null){
stack.push(cur.left);
}
}
}中序遍歷的遞迴實現
/**
* 中序遍歷
*/
public void inOrder(){
inOrder(root);
}
/**
* 遞迴的實現中序遍歷
* @param node 節點
*/
public void inOrder(Node node){
if(node == null)
return;
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}後序遍歷的遞迴實現
/**
* 後序遍歷
*/
public void postOrder(){
postOrder(root);
}
/**
* 遞迴的實現後序遍歷
* @param node 節點
*/
private void postOrder(Node node){
if(node == null)
return;
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
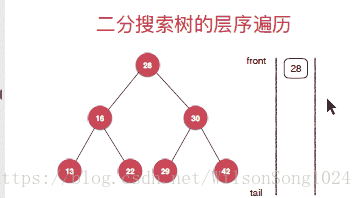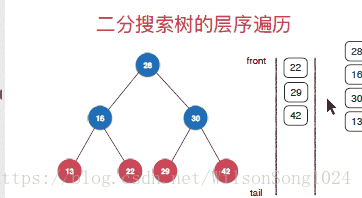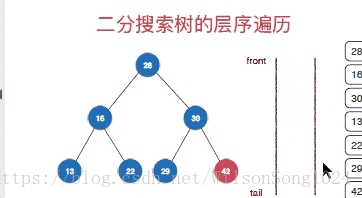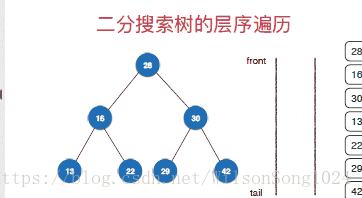
}廣度優先遍歷(層序遍歷)
層序遍歷的實現從根節點開,一次安深度往下遍歷,按照先左孩子然後右孩子的方式遍歷,這裡使用佇列的方式來實現層序遍歷,具體的實現方式如下:
/**
* 層序遍歷
*/
public void levelOrder(){
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()){
Node cur= queue.remove();
if (cur.left != null){
queue.add(cur.left);
}
if (cur.right != null){
queue.add(cur.right);
}
}
}刪除書中的節點
刪除樹中的最大元素和最小元素
首先是先要找到最大和最小元素,根據二分搜尋樹的性質我們可以很容易的就找到最大最小的元素
/**
* 查詢樹中最小元素
* @return
*/
public E minimum(){
if (size == 0){
throw new IllegalArgumentException("BST can not be empty");
}
return minimum(root).e;
}
/**
* 查詢樹中最小元素的節點
* @param node
* @return
*/
private Node minimum(Node node){
if (node.left == null){
return null;
}
return minimum(node.left);
}
/**
* 查詢樹中最大元素
* @return
*/
public E maximum(){
if (size == 0){
throw new IllegalArgumentException("BST can not be empty");
}
return maximum(root).e;
}
/**
* 查詢樹中最大元素的節點
* @param node
* @return
*/
private Node maximum(Node node){
if (node.right == null){
return node;
}
return maximum(node.right);
}找到了最大個最小元素之後要將其刪除,有需要注意的地方就是當樹的結構如下時:
從圖上我們可以看出,要是刪除的最小元素還有右孩子或者要刪除的最大元素還有左孩子的時候,就需要重新把待刪除元素的根節點指向其孩子節點。
具體的實現如下:
/**
* 查詢樹中最小元素
* @return
*/
public E minimum(){
if (size == 0){
throw new IllegalArgumentException("BST can not be empty");
}
return minimum(root).e;
}
/**
* 查詢樹中最小元素的節點
* @param node
* @return
*/
private Node minimum(Node node){
if (node.left == null){
return null;
}
return minimum(node.left);
}
/**
* 查詢樹中最大元素
* @return
*/
public E maximum(){
if (size == 0){
throw new IllegalArgumentException("BST can not be empty");
}
return maximum(root).e;
}
/**
* 查詢樹中最大元素的節點
* @param node
* @return
*/
private Node maximum(Node node){
if (node.right == null){
return node;
}
return maximum(node.right);
}
/**
* 刪除最小元素
* @return 返回最小元素的值
*/
public E removeMin(){
E ret = minimum();
root = removeMin(root);
return ret;
}
/**
* 刪除最小元素的節點,並返回刪除該節點之後新的二分搜尋樹的根
* @param node 樹節點
* @return
*/
public Node removeMin(Node node){
if (node.left == null && node.right != null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
/**
* 刪除最大元素,並返回最大元素的值
* @return
*/
public E removeMax(){
E ret = maximum();
root = removeMax(root);
return ret;
}
/**
* 刪除最大元素節點並返回刪除該節點之後新的二分搜尋樹的根
* @param node
* @return
*/
private Node removeMax(Node node){
if (node.right == null && node.left != null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}刪除樹中任意節點
刪除樹中任意的節點需要考慮的問題就多一些了
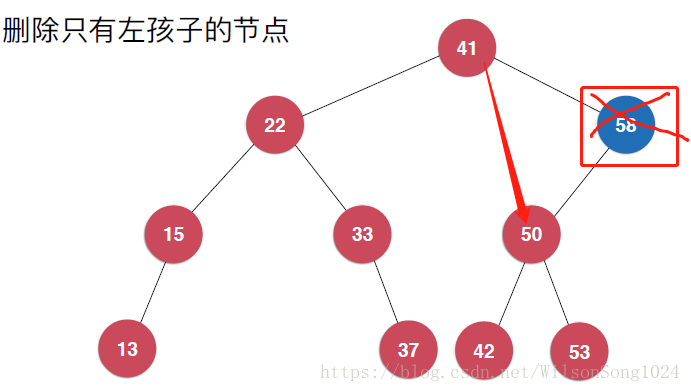
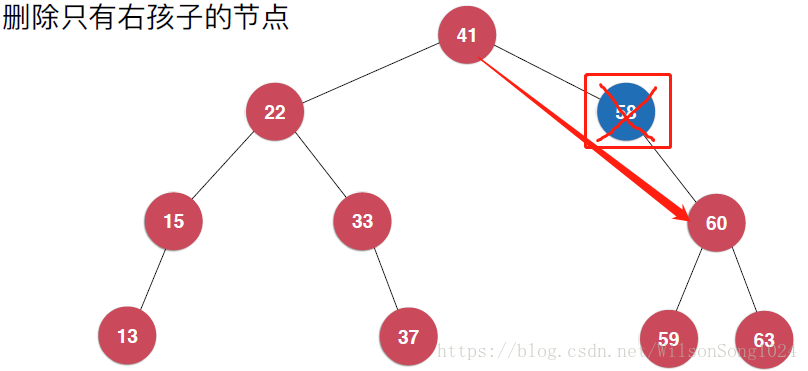
首先刪除的節點只有左孩子或者只有右孩子,這個時候其實是比較簡單的,刪除該節點後,其子節點有其父節點繼承即可。如下:
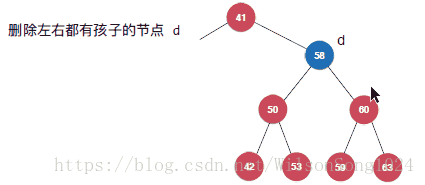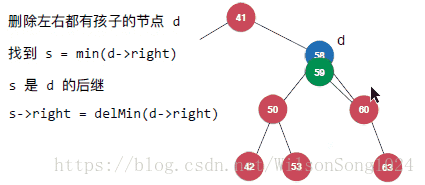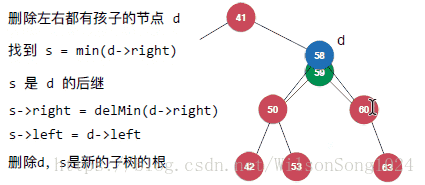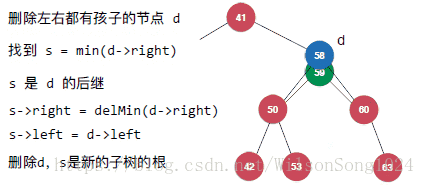
但是當要刪除的節點既有左孩子又有右孩子的時候就需要注意了,這裡使用Hibbard Deletion方法來實現,具體如下:
其實核心的思想即使找到該節點中右子樹中的最小節點來替代該節點成為新的節點。
具體的實現如下:
/**
* 從二分搜尋樹中刪除元素為e的節點
* @param e 刪除的元素
* @return
*/
public void remove(E e){
root = remove(root, e);
}
/**
* 刪除掉以node為根的二分搜尋樹中值為e的節點, 遞迴演算法,返回刪除節點後新的二分搜尋樹的根
* @param e 刪除的元素
*@param node 節點
* @return
*/
private Node remove(Node node, E e){
if( node == null )
return null;
if( e.compareTo(node.e) < 0 ){
node.left = remove(node.left , e);
return node;
}
else if(e.compareTo(node.e) > 0 ){
node.right = remove(node.right, e);
return node;
}
else{ // e.compareTo(node.e) == 0
// 待刪除節點左子樹為空的情況
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// 待刪除節點右子樹為空的情況
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// 待刪除節點左右子樹均不為空的情況
// 找到比待刪除節點大的最小節點, 即待刪除節點右子樹的最小節點
// 用這個節點頂替待刪除節點的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}注意
這裡刪除的操作為什麼需要返回刪除元素之後的新的樹的根節點其實和新增元素的道理是一樣的,可以參照一下。一樣的理解方式。
這樣就完成了樹的簡單的實現
拓展
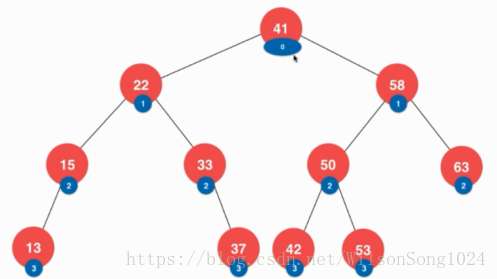
當然樹還有很多的東西可以去設計,比方說把每個樹的節點代表的含義設定的更加豐富
如:樹節點除了存值,還儲存以其為根節點的樹的元素的個數,也就是樹的size
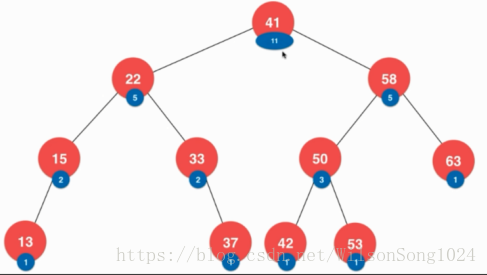
或者是儲存該節點在樹中的深度
或者是把樹設計成可以儲存重複的元素,就是在該節點在存一個代表其元素個數的值。
總之樹的拓展還有很多,待慢慢探索實現。