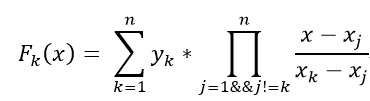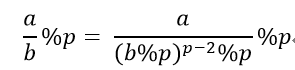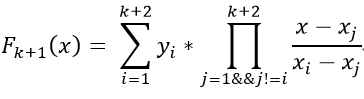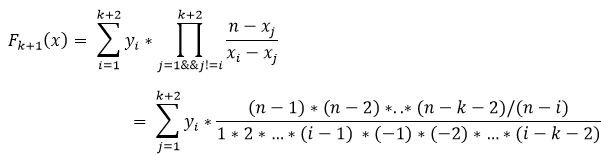做這個題之前需要知道一些知識:

拉格朗日插值:n-1次多項式可以用n個點唯一確定,插值公式是:

費馬小定理:a^(p-1)≡1(如果p是素數),也就是說模p時a和a^(p-2)互為逆元

關於模:當p是素數時

對於這道題可以發現對於每一個k次冪的積都可以用一個k+1次冪的多項式表示,於是我們可以構造出k+2個點來擬合這個多項式.拉格朗日插值公式在這裡就是:

我們需要求的就是F(n),帶入以後就是:

然後就是簡單的預處理和取模了,仔細點就可以了

#include <bits/stdc++.h>
using namespace std;
#define maxn 1000005
#define mod  1000000007

long long fac[maxn], y[maxn];
long long n, k;

long long qpow (long long a, long long b) {
    a %= mod, b %= mod;
    long long ans = 1;
    while (b) {
        if (b&1)
            ans = ans*a%mod;
        a = a*a%mod;
        b >>= 1;
    }
    return ans;
}

int main () {
    //freopen ("in.txt", "r", stdin);
    cin >> n >> k;
    fac[0] = 1;
    for (long long i = 1; i <= k+2; i++) {
        fac[i] = fac[i-1]*i%mod; 
    } 
    if (k == 0) {
        cout << n << endl;
        return 0;
    }
    y[0] = 0;
    for (long long i = 1; i <= k+2; i++) {
        y[i] = y[i-1]+qpow (i, k); 
        y[i] %= mod;
    } 
    if (n <= k+2) {
        cout << y[n] << endl;
        return 0;
    }
    long long ans1 = 1;
    for (long long i = n-k-2; i <= n-1; i++) ans1 = ans1*i%mod;
    long long ans = 0;
    for (long long i = 1; i <= k+2; i++) {
        long long p1 = qpow (n-i, mod-2)%mod;
        long long p2 = qpow (fac[i-1]*fac[k+2-i]%mod, mod-2)%mod;
        long long sign = ((k+2-i)%2 == 1 ? -1 : 1);
        long long cur = y[i]*p1%mod*p2%mod*ans1%mod;
        cur *= sign;
        if (cur < 0)
            cur = (cur+mod)%mod;
        ans = (ans+cur)%mod;
    }
    cout << ans << endl;
    return 0;
}