點到向量距離(含Python程式碼)
向量間投影和距離
這段時間用到了點到向量的距離,發現已經還給高數老師了。借這篇部落格(參考英文部落格)總結回顧一下,並且附上Python程式碼。先回顧下向量點積和叉乘公式,
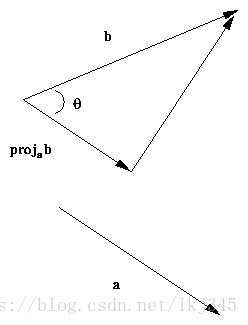
從下圖可以看出b向量在a向量上的投影長度是
點到向量的距離
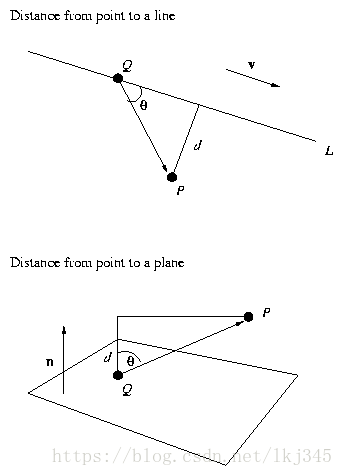
考慮下圖中上半部分,求點P到直線L的距離,其中L的方向向量是v。任取直線上一點Q,
通過叉乘的計算公式(如下圖,聯想行列式計算公式),我們可知

Python程式
可以通過Python指令碼模擬上述過程,程式碼如下。
import numpy as np
QP = np.array 相關推薦
點到向量距離(含Python程式碼)
向量間投影和距離 這段時間用到了點到向量的距離,發現已經還給高數老師了。借這篇部落格(參考英文部落格)總結回顧一下,並且附上Python程式碼。先回顧下向量點積和叉乘公式,a⋅b=|a||b|cos(θ)a⋅b=|a||b|cos(θ),a×b=|a||b|s
12種降維方法終極指南(含Python程式碼)
你遇到過特徵超過1000個的資料集嗎?超過5萬個的呢?我遇到過。降維是一個非常具有挑戰性的任務,尤其是當你不知道該從哪裡開始的時候。擁有這麼多變數既是一個恩惠——資料量越大,分析結果越可信;也是一種詛咒——你真的會感到一片茫然,無從下手。 面對這麼多特徵,在微觀層面分析每個
OpenCV 3計算機視覺 Python語言實現(第2版)(含示例程式碼)PDF
OpenCV 3計算機視覺 Python語言實現(第2版)(含示例程式碼) 建議購買正版,支援作者 完整pdf下載 百度網盤 連結:https://pan.baidu.com/s/1kUYNN66nsVWBB5Y5cZ06kw 提取碼:u7nv 原始碼下載地址 完整專案
OpenCV 3計算機視覺 Python語言實現(第2版)(含示例程式碼)
http://blog.csdn.net/wyx100/article/details/73006307 建議購買正版,支援作者 書籍閱讀pdf 完整pdf下載 手機版本下載 原始碼下載地址 完整專案 原始碼+圖片+資料
計算機視覺之(一)利用Harris檢測子進行角點特徵檢測(含matlab原始碼)
本文為原創文章,轉載請註明本文來自http://blog.csdn.net/anymake_ren/article/details/21298807 計算機視覺中常用的影象特徵包括:點、
視訊監控專案(含完整程式碼)
功能簡介: 採集端: 1.USB攝像頭採集資料(yuyv格式),通過v4l2 API。 2. 資料格式轉換,yuyv->yuv420p. 3.h264編碼壓縮.通過x264編碼庫 4.資料傳輸(tcp)。
使用條件隨機場模型解決文字分類問題(附Python程式碼)
對深度學習感興趣,熱愛Tensorflow的小夥伴,歡迎關注我們的網站!http://www.tensorflownews.com。我們的公眾號:磐創AI。 一. 介紹 世界上每天都在生成數量驚人的文字資料。Google每秒處理超過40,000次搜尋,而根據福布斯報道,
Robust PCA——Inexect ALM(含python實現)
原文:https://blog.csdn.net/u010510350/article/details/77885553 前兩篇部落格已經介紹了Robust PCA及RPCA的優化,接下來用Robust PCA實現背景建模。背景建模就是將攝像機獲取的場景分離出前景和背景,以獲取場景中的動態目
瞧一瞧!這兒實現了MongoDB的增量備份與還原(含部署程式碼)
一 需求描述 我們知道資料是公司的重要資產,業務的系統化、資訊化就是數字化。資料高效的儲存與查詢是系統完善和優化的方向,而資料庫的穩定性、可靠性是實現的基礎。高可用和RPO(RecoveryPointObjective,復原點目標,指能容忍的最大資料丟失量)是衡量一個數據庫優劣的重要指標。作為一個DBA,搭
利用Python實現卷積神經網路的視覺化(附Python程式碼)
對於深度學習這種端到端模型來說,如何說明和理解其中的訓練過程是大多數研究者關注熱點之一,這個問題對於那種高風險行業顯得尤為重視,比如醫療、軍事等。在深度學習中,這個問題被稱作“黑匣子(Black Box)”。如果不能解釋模型的工作過程,我們怎麼能夠就輕易相信模型的輸出結果呢? 以深度學習模型檢測
整合學習-模型融合學習筆記(附Python程式碼)
1 整合學習概述 整合學習(Ensemble Learning)是一種能在各種的機器學習任務上提高準確率的強有力技術,其通過組合多個基分類器(base classifier)來完成學習任務。基分類器一般採用的是弱可學習(weakly learnable)分類器,通過整合學習
偏度與峰度(附python程式碼)
1 矩 對於隨機變數X,X的K階原點矩為 X的K階中心矩為 期望實際上是隨機變數X的1階原點矩,方差實際上是隨機變數X的2階中心矩 變異係數(Coefficient of Variation):標準差與均值(期望)的比值稱為變異係數,記為C
資料結構-順序棧的基本操作的實現(含全部程式碼)
主要操作函式如下: InitStack(SqStack &s) 引數:順序棧s 功能:初始化 時間複雜度O(1) Push(SqStack &s,SElemType e) 引數:順序棧s,元素e 功能:將e入棧 時間複雜度:O(1)
資料結構-迴圈佇列的基本操作函式實現(含全部程式碼)
主要包含以下函式: InitQueue(SqQueue &Q) 引數:迴圈佇列Q 功能:初始化迴圈佇列Q 時間複雜度:O(1) QueueEmpty(SqQueue Q) 引數:迴圈佇列Q
資料結構-鏈隊的基本操作函式的實現(含全部程式碼)
主要包含以下函式: InitQueue(LinkQueue &Q) 引數:鏈隊Q 功能:初始化 時間複雜度O(1) EnQueue(LinkQueue &Q,QElemType e) 引數:鏈隊Q,元素e 功能:將e入隊 時間複雜度
資料結構-簡單選擇排序(含全部程式碼)
函式分析如下: SelectSort(SqList &L) 引數:順序表L 功能:排序(預設升序)空間複雜度:O(1) 時間複雜度:O(n方) 穩定性:不穩定 思想:假設第i個值為當前最小值(0到i-1已經為
機器學習系列(12)_XGBoost引數調優完全指南(附Python程式碼)
1. 簡介 如果你的預測模型表現得有些不盡如人意,那就用XGBoost吧。XGBoost演算法現在已經成為很多資料工程師的重要武器。它是一種十分精緻的演算法,可以處理各種不規則的資料。 構造一個使用XGBoost的模型十分簡單。但是,提高這個模型的表現就有些困難(至少我
基於Redis的Bloomfilter去重(附Python程式碼)
“去重”是日常工作中會經常用到的一項技能,在爬蟲領域更是常用,並且規模一般都比較大。去重需要考慮兩個點:去重的資料量、去重速度。為了保持較快的去重速度,一般選擇在記憶體中進行去重。 資料量不大時,可以直接放在記憶體裡面進行去重,例如python可以使用set()
C++虛擬函式表(含測試程式碼)
自己搞不懂C++虛擬函式之間的呼叫關係,特地花費一個下午加一個晚上查資料學習,現在把學到的發上來,供大家學習批評; 在此之前感謝這些大佬的部落格等,為我解惑甚多: 1、虛表與虛表指標 C++中的虛擬函式的實現一般是通過虛擬函式表(V-Table)來實
BAT機器學習特徵工程工作經驗總結(一)如何解決資料不平衡問題(附python程式碼)
很多人其實非常好奇BAT裡機器學習演算法工程師平時工作內容是怎樣?其實大部分人都是在跑資料,各種map-reduce,hive SQL,資料倉庫搬磚,資料清洗、資料清洗、資料清洗,業務分析、分析case、找特徵、找特徵…而複雜的模型都是極少數的資料科學家在做。例