到2018年3月7日為止，本系列三篇文章已寫完，可能後續有新的內容的話會繼續更新。

本篇是我的LDA主題挖掘系列的第三篇，專門來介紹如何對訓練好的LDA模型進行評價。

訓練好好LDA主題模型後，如何評價模型的好壞？能否直接將訓練好的模型拿去應用？這是一個比較重要的問題，在對模型精度要求比較高的專案或科研中，需要對模型進行評價。一般來說，LDA模型的主題數量都是需要需要根據具體任務進行調整的，即要評價不同主題數的模型的困惑度來選擇最優的那個模型。

那麼，困惑度是什麼？
1.LDA主題模型困惑度
這部分參照：LDA主題模型評估方法–Perplexity，不過後面發現這篇文章

Perplexity(困惑度)感覺寫的更好一點，兩篇都是翻譯的維基百科。
perplexity是一種資訊理論的測量方法，b的perplexity值定義為基於b的熵的能量（b可以是一個概率分佈，或者概率模型），通常用於概率模型的比較
wiki上列舉了三種perplexity的計算：
1.1 概率分佈的perplexity
公式：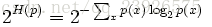
其中H(p)就是該概率分佈的熵。當概率P的K平均分佈的時候，帶入上式可以得到P的perplexity值=K。
1.2 概率模型的perplexity
公式：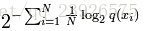
公式中的Xi為測試局，可以是句子或者文字，N是測試集的大小（用來歸一化），對於未知分佈q，perplexity的值越小，說明模型越好。
指數部分也可以用交叉熵來計算，略過不表。
1.3單詞的perplexity
perplexity經常用於語言模型的評估，物理意義是單詞的編碼大小。例如，如果在某個測試語句上，語言模型的perplexity值為2^190，說明該句子的編碼需要190bits
2.困惑度perplexity公式

perplexity=e−∑log(p(w))N$$perplexity=e^{\frac{-\sum log(p(w))}{N}}$$
其中，p(w)是指的測試集中出現的每一個詞的概率，具體到LDA的模型中就是p(w)=∑zp(z|d)∗p(w|z)$p(w)=\sum zp(z|d)\ast p(w|z)$ (z,d分別指訓練過的主題和測試集的各篇文件)。分母的N是測試集中出現的所有詞，或者說是測試集的總長度，不排重。
3.計算困惑度的程式碼

下述程式碼中載入的.dictionary(字典)、.mm(語料)、.model(模型)檔案均為在python下進行lda主題挖掘(二)——利用gensim訓練LDA模型中得到的結果，如果檔案格式與我不同，說明呼叫的不是同一個包，程式碼無法直接使用，可參考程式碼邏輯，若是已按照

python下進行lda主題挖掘(二)——利用gensim訓練LDA模型中的方法得到上述檔案，可直接呼叫下述程式碼計算困惑度。
PS：將語料經過TFIDF訓練模型後計算得到的困惑度要遠大於直接進行訓練的困惑度（在我這邊是這樣），應該是正常情況，不必驚慌。

#-*-coding:utf-8-*-
import sys
reload(sys)
sys.setdefaultencoding('utf-8')
import os
from gensim.corpora import Dictionary
from gensim import corpora, models
from datetime import datetime
import logging
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s : ', level=logging.INFO)

def perplexity(ldamodel, testset, dictionary, size_dictionary, num_topics):
    """calculate the perplexity of a lda-model"""
    # dictionary : {7822:'deferment', 1841:'circuitry',19202:'fabianism'...]
    print ('the info of this ldamodel: \n')
    print ('num of testset: %s; size_dictionary: %s; num of topics: %s'%(len(testset), size_dictionary, num_topics))
    prep = 0.0
    prob_doc_sum = 0.0
    topic_word_list = [] # store the probablity of topic-word:[(u'business', 0.010020942661849608),(u'family', 0.0088027946271537413)...]
    for topic_id in range(num_topics):
        topic_word = ldamodel.show_topic(topic_id, size_dictionary)
        dic = {}
        for word, probability in topic_word:
            dic[word] = probability
        topic_word_list.append(dic)
    doc_topics_ist = [] #store the doc-topic tuples:[(0, 0.0006211180124223594),(1, 0.0006211180124223594),...]
    for doc in testset:
        doc_topics_ist.append(ldamodel.get_document_topics(doc, minimum_probability=0))
    testset_word_num = 0
    for i in range(len(testset)):
        prob_doc = 0.0 # the probablity of the doc
        doc = testset[i]
        doc_word_num = 0 # the num of words in the doc
        for word_id, num in doc:
            prob_word = 0.0 # the probablity of the word 
            doc_word_num += num
            word = dictionary[word_id]
            for topic_id in range(num_topics):
                # cal p(w) : p(w) = sumz(p(z)*p(w|z))
                prob_topic = doc_topics_ist[i][topic_id][1]
                prob_topic_word = topic_word_list[topic_id][word]
                prob_word += prob_topic*prob_topic_word
            prob_doc += math.log(prob_word) # p(d) = sum(log(p(w)))
        prob_doc_sum += prob_doc
        testset_word_num += doc_word_num
    prep = math.exp(-prob_doc_sum/testset_word_num) # perplexity = exp(-sum(p(d)/sum(Nd))
    print ("the perplexity of this ldamodel is : %s"%prep)
    return prep

if __name__ == '__main__':
    middatafolder = r'E:\work\lda' + os.sep
    dictionary_path = middatafolder + 'dictionary.dictionary'
    corpus_path = middatafolder + 'corpus.mm'
    ldamodel_path = middatafolder + 'lda.model'
    dictionary = corpora.Dictionary.load(dictionary_path)
    corpus = corpora.MmCorpus(corpus_path)
    lda_multi = models.ldamodel.LdaModel.load(ldamodel_path)
    num_topics = 50
    testset = []
    # sample 1/300
    for i in range(corpus.num_docs/300):
        testset.append(corpus[i*300])
    prep = perplexity(lda_multi, testset, dictionary, len(dictionary.keys()), num_topics)

參考資料

以上，歡迎交流。
程式碼略為粗糙，如有問題，請務必指正，感激不盡。