GIS 地圖座標系相互轉換的方法學習筆記

一，前言

任何一個國家（或地區）大地座標系的建立，都是一個歷史的發展過程，在不同的時期，採用的參考橢球體及定位方式都不相同，並且會逐步的完善和精化。採用不同的參考橢球和定位建立的大地座標系，是彼此不同的參心空間直角座標系，與全球統一的以地球質心為原點的地心空間直角座標系也不一致。因此就存在不同的大地座標系統之間的相互轉換問題。
我在專案中使用的是SuperMap的SDK，所以這裡就用SuperMap的SDK進行學習。

二，GIS座標系背景

1、基本概念

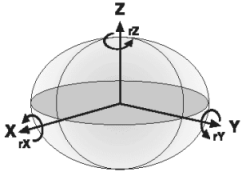
地球是一個近似橢球體，測繪時用橢球模型逼近，這個模型叫做參考橢球，如下圖：

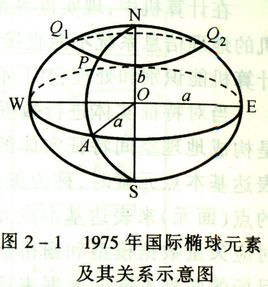
赤道是一個半徑為a的近似圓，任一圈經線是一個半徑為b的近似圓。a稱為橢球的長軸半徑，b稱為橢球的短軸半徑。

a≈6378.137千米，b≈6356.752千米。（實際上，a也不是恆定的，最長處和最短處相差72米，b的最長處和最短處相差42米，算很小了）

地球參考橢球基本引數：

長軸：a

短軸：b

扁率：α=(a-b) / a

第一偏心率：e=√(a2-b2) / a

第二偏心率：e’=√(a2-b2) / b

這幾個引數定了，參考橢球的數學模型就定了。

座標系有

地理座標系：為球面座標。 參考平面地是橢球面，座標單位：經緯度；

投影座標系：為平面座標。參考平面地是水平面，座標單位：米、千米等；

地理座標轉換到投影座標的過程可理解為投影。（投影：將不規則的地球曲面轉換為平面）

2、地理座標系

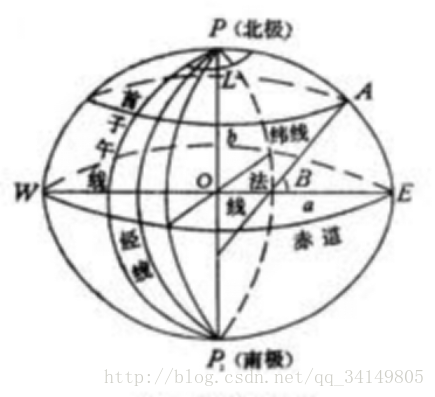
地理座標，就是用經線（子午線）、緯線、經度、緯度表示地面點位的球面座標。

一般地理座標可分為三種，天文經緯度，大地經緯度，地心經緯度。通常地圖上使用的經緯度都為大地經緯度，所以這裡我介紹一下大地經緯度，其他兩種要想了解的話可以百度一下，其實區別不大。

大地經緯度：

大地經度：參考橢球面上某點的大地子午面與本初子午面間的兩面角。東正西負。

大地緯度 ：參考橢球面上某點的法線與赤道平面的夾角。北正南負。

大地高： 指某點沿法線方向到參考橢球面的距離。

3、投影座標系

在地球橢球面和平面之間建立點與點之間函式關係的數學方法，稱為地圖投影。

地球橢球表面是一種不可能展開的曲面，要把這樣一個曲面表現到平面上，就會發生裂隙或褶皺。在投影面上，可運用經緯線的“拉伸”或“壓縮”（通過數學手段）來加以避免，以便形成一幅完整的地圖。但不可避免會產生變形。
地圖投影的變形通常有：長度變形、面積變形和角度變形。在實際應用中，根據使用地圖的目的，限定某種變形。

根據不同的需要，我們會選擇不同的投影組合！

按變形性質分類：
等角投影：角度變形為零（Mercator）
等積投影：面積變形為零（Albers）
任意投影：長度、角度和麵積都存在變形 
其中，各種變形相互聯絡相互影響：等積與等角互斥，等積投影角度變形大，等角投影面積變形大。
從投影面型別劃分：

橫圓柱投影：投影面為橫圓柱
圓錐投影：投影面為圓錐
方位投影：投影面為平面
從投影面與地球位置關係劃分為：

正軸投影：投影面中心軸與地軸相互重合
斜軸投影：投影面中心軸與地軸斜向相交
橫軸投影：投影面中心軸與地軸相互垂直
相切投影：投影面與橢球體相切
相割投影：投影面與橢球體相割

投影引數：
標準線 
概念：投影面與參考橢球的切線或割線。分為標準緯線與標準經線。 
特點：沒有變形，也稱主比例尺。
中心線 
概念：是指中央經線（原點經線）與中央緯線（原點緯線），用來定義圖投影的中心或者原點。 
特點：一般會有變形。

4，常用座標系

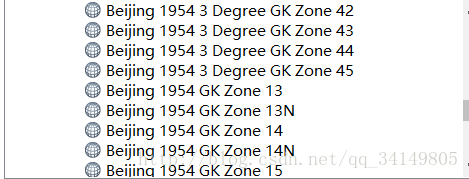
我們在選擇座標系的時候經常會發現以下情況：

這一大堆1954座標系究竟是什麼鬼,beijing1954不是地理座標系嗎？

為什麼投影座標系裡也有？相信懵逼的不止我一個···

首先，投影座標系的生成是以地理座標系為基準的，所以每個投影座標系前面都會掛有地理座標系。而地理座標系後面的一串亂七八糟的，則是投影引數！

比如 Beijing 1954 3 Degree GK Zone 39

意思是

3度分帶法的北京54座標系，中央經線在東117度的分帶座標，橫座標前加帶號。

詳細請檢視
https://blog.csdn.net/engineer_he/article/details/74910434
https://blog.csdn.net/qq_34149805/article/details/65634252

三，座標的參照系之間轉換

地理座標系（Geographic Coordinate System）也稱為地理座標系統，是以經緯度為地圖的儲存單位的。很明顯，地理座標系是球面座標系統。如果將地球上的數字化資訊存放到球面座標系統上，就需要有這樣的橢球體具有如下特點：可以量化計算的，具有長半軸（Semimajor Axis），短半軸（Semiminor Axis），偏心率（Flattening），中央子午線（prime meridian）及大地基準面（datum）。投影座標系統（Projection coordinate system）實質上便是平面座標系統，其地圖單位通常為米。將球面座標轉化為平面座標的過程便稱為投影。所以每一個投影座標系統都必定會有地理座標系統（Geographic Coordinate System）引數。 因此就存在著投影座標之間的轉換以及投影座標系之間的轉換。

SuperMap中CoordSysTranslator是進行座標轉換工具類

1，地理座標和投影座標之間的轉換

這種轉換在SuperMap中封裝了兩個介面

static boolean forward(Point2Ds points, PrjCoordSys prjCoordSys) 
          在同一地理座標系下，該方法用於將指定的Point2Ds 類的點物件的地理座標轉換到投影座標。 
static boolean inverse(Point2Ds points, PrjCoordSys prjCoordSys) 
          在同一投影座標系下，該方法用於將指定的Point2Ds 類的點物件的投影座標轉換到地理座標。 

相關類的介紹

PrjCoordSys
投影座標系類。

投影座標系統由地圖投影方式、投影引數、座標單位和地理座標系組成。SuperMap iMobile for Android 中提供了很多預定義的投影系統，使用者可以直接使用，此外，使用者還可以定製自己投影系統。

投影座標系是定義在二維平面上的，不同於地理座標系用經緯度定位地面點，投影座標系是用 X、Y 座標來定位的。每一個投影座標系都基於一個地理座標系。

GeoCoordSys
地理座標系類。

地理座標系由大地參照系、中央子午線、座標單位組成。在地理座標系中，單位一般用度來表示，也可以用度分秒錶示。東西向（水平方向）的範圍為-180度至180度。 南北向（垂直方向）的範圍為-90度至90度。

地理座標是用經緯度表示地面點位置的球面座標。在球形系統中，赤道面的平行面同地球橢球面相交所截的圈稱為緯圈，也叫緯線，表示東西方向， 通過地球旋轉軸的面與橢球面相交所截的圈為子午圈，也稱經線，表示南北方向，這些包圍著地球的網格稱為經緯格網。經緯線一般用度來表示（必要時也用度分秒錶示）， 經緯度是從地心到地球表面相應的位置的角度的大小表示的。

地理座標和投影座標之間的轉換就是投影和反投影的過程。

另外 因為投影座標是一個平面座標系，所以在某些情況下為了更精確的定位位置會對平面座標進行一些位置的糾偏。

一般簡單的會有一下幾個引數的校準，還有些比較複雜的就沒有了解了。

1. dx X軸的偏移量
2. dy Y軸的偏移量
3. rangle 座標系的旋轉角度
4. scale 座標系的縮放比例
5. dz 當有高度要求的時候也可以新增高度的偏移量

如果投影座標是需要進行校準時，在進行轉換是需要把這些校準引數新增上去。

例如 ：地理座標轉換到投影座標

1. 呼叫forward方法把地理點轉換到投影座標點
2. 如果有垂直校準就對點進行垂直校準
3. 對投影點進行角度的旋轉計算對投影點進行角度的旋轉計算
4. 根據縮放比例進行縮放的計算
5. 對x，y軸偏移量進行計算

2，參照系轉換

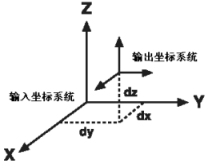
當進行資料來源投影轉換或點座標轉換時，SuperMap提供了六種投影轉化的方法（Geocentric Transalation、Molodensky、MolodenskyAbridged 、Position Vector、Coordinate Frame、Bursa-wolf）。以上六種轉換方法，按照轉換引數的多少可以分為兩類：三引數轉換法和七引數轉換法。

三引數轉換法
參照系轉換時，比較簡單的轉換方法是所謂的三引數轉換法。這種轉化方法所依據的數學模型是認為兩種大地參照系之間僅僅是空間的座標原點發生了平移，而不考慮其他因素（見圖1）。這種方法必然產生三個引數，X 、Y、Z 三個方向的平移量。三引數轉換法計算簡單，但精度較低，一般用在不同的地心空間直角座標系之間的轉換。

七引數轉換法
七引數法依據的數學模型不僅考慮了座標系的平移，同時還考慮了座標系旋轉、尺度不一等因素。所以需要的引數除了三個平移量外，還要三個旋轉引數（又稱三個尤拉角）和比例因子（又叫尺度因子）。轉換原理如圖2所示。三個平移量用ΔX、ΔY、ΔZ 表示，三個選擇引數用 Rx，Ry，Rz 表示；比例因子用 S 表示。其中比例因子表示從原座標系轉換到新座標系的尺度伸縮量。一般情況下，平移因子的單位為米（與座標系單位保持一致），旋轉因子的單位是秒，比例因子的單位為百萬分之一。

目前，支援6種投影轉換的方法，方便使用者根據不同的需求，選擇合適轉換方法。

地心轉換法(the Geocentric Translation)、莫洛金斯基轉換法（Molodensky）、簡化的莫洛金斯（MolodenskyAbridged）轉換法屬於精度較低的投影轉換方法。三引數轉換法需要三個平移轉換引數（ΔX，ΔY，ΔZ），莫洛金斯基轉換法、簡化的莫洛金斯基轉換法也要三個平移轉換引數（ΔX，ΔY，ΔZ）。在資料精度要求不高的情況下一般可以採用這幾種方法。

位置向量法（Position Vector）、基於地心的七引數轉換法（Coordinate Frame）、布林莎方法（Bursa-Wolf）屬於精度較高的幾種轉換方法。需要七個引數來進行調整和轉換，包括三個平移轉換引數（ΔX，ΔY，ΔZ）、三個旋轉轉換引數（Rx，Ry，Rz）和一個比例引數（S）。這幾種方法是完全相同的，只是由於國家地區或測量學派的不同，習慣稱謂不同。

總結

兩個不同的投影座標A，B之間進行簡單轉換的過程如下：