用了之後，發現我用的都是1NN，所以查閱了一下相關文獻，才對KNN理解正確了，真是丟人了。

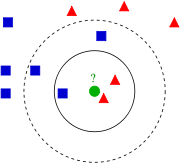
左圖中，綠色圓要被決定賦予哪個類，是紅色三角形還是藍色四方形？如果K=3，由於紅色三角形所佔比例為2/3，綠色圓將被賦予紅色三角形那個類，如果K=5，由於藍色四方形比例為3/5，因此綠色圓被賦予藍色四方形類。

K最近鄰(k-Nearest Neighbor，KNN)分類演算法，是一個理論上比較成熟的方法，也是最簡單的機器學習演算法之一。該方法的思路是：如果一個樣本在特徵空間中的k個最相 似(即特徵空間中最鄰近)的樣本中的大多數屬於某一個類別，則該樣本也屬於這個類別。KNN演算法中，所選擇的鄰居都是已經正確分類的物件。該方法在定類決 策上只依據最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。 KNN方法雖然從原理上也依賴於極限定理，但在類別決策時，只與極少量的相鄰樣本有關。由於KNN方法主要靠周圍有限的鄰近的樣本，而不是靠判別類域的方 法來確定所屬類別的，因此對於類域的交叉或重疊較多的待分樣本集來說，KNN方法較其他方法更為適合。

其 中，x為一篇待分類網頁的向量表示；di為訓練集中的一篇例項網頁的向量表示；cj為一類別；（當d屬於c}1,0{),(∈jicdyj時取1；當不屬 於cdj時取0）；bj為預先計算得到的cj的最優截尾閾值；為待分類網頁與網頁例項之間的相似度，由文件間的餘弦相似度公式（11-10）計算得到：

kNN演算法本身簡單有效，它是一種lazy-learning演算法，分類器不需要使用訓練集進行訓練，訓練時間複雜度為0。kNN分類的計算複雜度和訓練集中的文件數目成正比，也就是說，如果訓練集中文件總數為n，那麼kNN的分類時間複雜度為O(n)。

KNN演算法不僅可以用於分類，還可以用於迴歸。通過找出一個樣本的k個最近鄰居，將這些鄰居的屬性的平均值賦給該樣本，就可以得到該樣本的屬性。更有用的方法是將不同距離的鄰居對該樣本產生的影響給予不同的權值(weight)，如權值與距離成正比。

該演算法在分類時有個主要的不足是，當樣本不平衡時，如一個類的樣本容量很大，而其他類樣本容量很小時，有可能導致當輸入一個新樣本時，該樣本的 K個鄰居中大容量類的樣本佔多數。因此可以採用權值的方法（和該樣本距離小的鄰居權值大）來改進。該方法的另一個不足之處是計算量較大，因為對每一個待分 類的文字都要計算它到全體已知樣本的距離，才能求得它的K個最近鄰點。目前常用的解決方法是事先對已知樣本點進行剪輯，事先去除對分類作用不大的樣本。該 演算法比較適用於樣本容量比較大的類域的自動分類，而那些樣本容量較小的類域採用這種演算法比較容易產生誤分。