BTree和B+Tree詳解
B
樹是為了磁碟或其它儲存裝置而設計的一種多叉(下面你會看到,相對於二叉,B樹每個內結點有多個分支,即多叉)平衡查詢樹。
B 樹又叫平衡多路查詢樹。一棵m階的B 樹 (m叉樹)的特性如下:
- 樹中每個結點最多含有m個孩子(m>=2);
- 除根結點和葉子結點外,其它每個結點至少有[ceil(m / 2)]個孩子(其中ceil(x)是一個取上限的函式);
- 若根結點不是葉子結點,則至少有2個孩子(特殊情況:沒有孩子的根結點,即根結點為葉子結點,整棵樹只有一個根節點);
- 所有葉子結點都出現在同一層,葉子結點不包含任何關鍵字資訊(可以看做是外部接點或查詢失敗的接點,實際上這些結點不存在,指向這些結點的指標都為null);
-
每個非終端結點中包含有n個關鍵字資訊: (P1,K1,P2,K2,P3,......,Kn,Pn+1)。其中:
a) Ki (i=1...n)為關鍵字,且關鍵字按順序升序排序K(i-1)< Ki。
b) Pi為指向子樹根的接點,且指標P(i)指向子樹種所有結點的關鍵字均小於Ki,但都大於K(i-1)。
c) 關鍵字的個數n必須滿足: [ceil(m / 2)-1]<= n <= m-1。
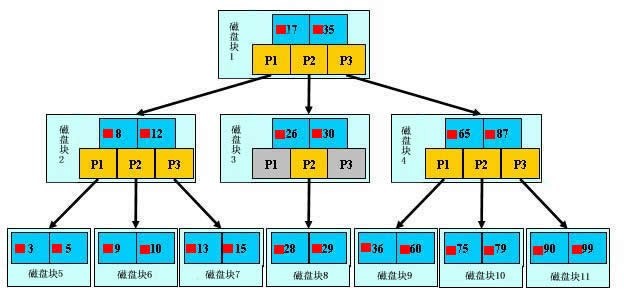
來模擬下查詢檔案29的過程:
(1) 根據根結點指標找到檔案目錄的根磁碟塊1,將其中的資訊匯入記憶體。【磁碟IO操作1次】
(2) 此時記憶體中有兩個檔名17,35和三個儲存其他磁碟頁面地址的資料。根據演算法我們發現17<29<35,因此我們找到指標p2。
(3) 根據p2指標,我們定位到磁碟塊3,並將其中的資訊匯入記憶體。【磁碟IO操作2次】
(4) 此時記憶體中有兩個檔名26,30和三個儲存其他磁碟頁面地址的資料。根據演算法我們發現26<29<30,因此我們找到指標p2。
(5) 根據p2指標,我們定位到磁碟塊8,並將其中的資訊匯入記憶體。【磁碟IO操作3次】
(6) 此時記憶體中有兩個檔名28,29。根據演算法我們查詢到檔案29,並定位了該檔案記憶體的磁碟地址。
插入操作
生 成從空樹開始,逐個插入關鍵字。但是由於B_樹節點關鍵字必須大於等於[ceil(m/2)-1],所以每次插入一個關鍵字不是在樹中新增一個葉子結點, 而是首先在最底層的某個非終端節點中新增一個“關鍵字”,該結點的關鍵字不超過m-1,則插入完成;否則要產生結點的“分裂”,將一半數量的關鍵字元素分裂到新的其相鄰右結點中,中間關鍵字元素上移到父結點中。
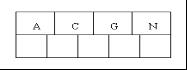
1、咱們通過一個例項來逐步講解下。插入以下字元字母到一棵空的B 樹中(非根結點關鍵字數小了(小於2個)就合併,大了(超過4個)就分裂):C N G A H E K Q M F W L T Z D P R X Y S,首先,結點空間足夠,4個字母插入相同的結點中,如下圖:
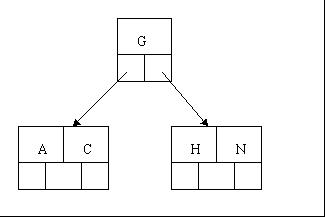
2、當咱們試著插入H時,結點發現空間不夠,以致將其分裂成2個結點,移動中間元素G上移到新的根結點中,在實現過程中,咱們把A和C留在當前結點中,而H和N放置新的其右鄰居結點中。如下圖:
3、當咱們插入E,K,Q時,不需要任何分裂操作
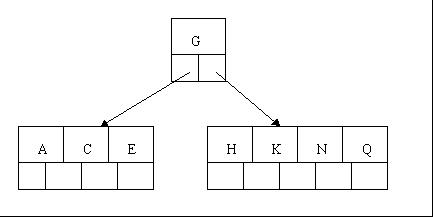
4、插入M需要一次分裂,注意M恰好是中間關鍵字元素,以致向上移到父節點中
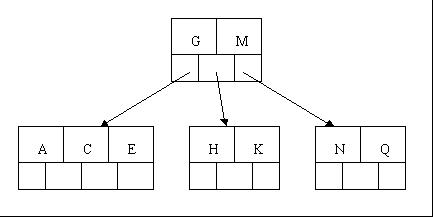
5、插入F,W,L,T不需要任何分裂操作
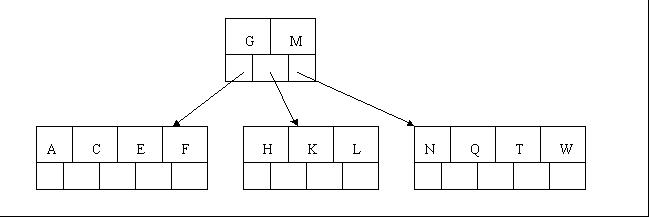
6、插入Z時,最右的葉子結點空間滿了,需要進行分裂操作,中間元素T上移到父節點中,注意通過上移中間元素,樹最終還是保持平衡,分裂結果的結點存在2個關鍵字元素。

7、插入D時,導致最左邊的葉子結點被分裂,D恰好也是中間元素,上移到父節點中,然後字母P,R,X,Y陸續插入不需要任何分裂操作(別忘了,樹中至多5個孩子)。
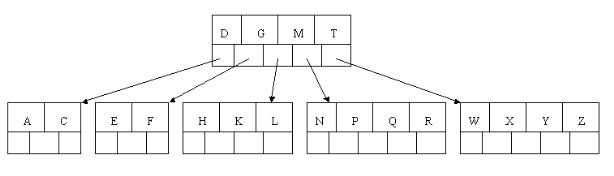
8、最後,當插入S時,含有N,P,Q,R的結點需要分裂,把中間元素Q上移到父節點中,但是情況來了,父節點中空間已經滿了,所以也要進行分裂,將父節點中的中間元素M上移到新形成的根結點中,注意以前在父節點中的第三個指標在修改後包括D和G節點中。這樣具體插入操作的完成。
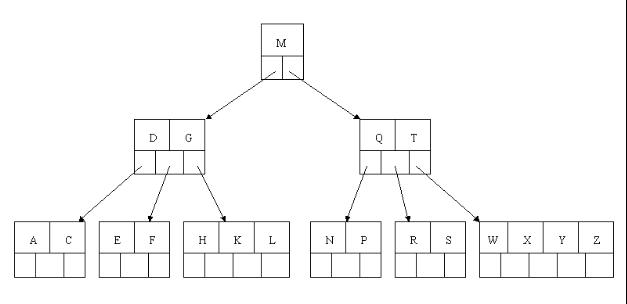
刪除操作
首先查詢B樹中需刪除的元素,如果該元素在B樹中存在,則將該元素在其結點中進行刪除,如果刪除該元素後,首先判斷該元素是否有左右孩子結點,如果有,則上移孩子結點中的某相近元素到父節點中,然後是移動之後的情況;如果沒有,直接刪除後,移動之後的情況。
刪除元素,移動相應元素之後,如果某結點中元素數目(即關鍵字數)小於ceil(m/2)-1,則需要看其某相鄰兄弟結點是否豐滿(結點中元素個數大於ceil(m/2)-1)(還記得第一節中關於B樹的第5個特性中的c點麼?: c)除根結點之外的結點(包括葉子結點)的關鍵字的個數n必須滿足: (ceil(m / 2)-1)<= n <= m-1。m表示最多含有m個孩子,n表示關鍵字數。在本小節中舉的一顆B樹的示例中,關鍵字數n滿足:2<=n<=4),如果豐滿,則向父節點借一個元素來滿足條件;如果其相鄰兄弟都剛脫貧,即借了之後其結點數目小於ceil(m/2)-1,則該結點與其相鄰的某一兄弟結點進行“合併”成一個結點,以此來滿足條件。那咱們通過下面例項來詳細瞭解吧。
以上述插入操作構造的一棵5階B樹(樹中最多含有m(m=5)個孩子,因此關鍵字數最小為ceil(m / 2)-1=2。還是這句話,關鍵字數小了(小於2個)就合併,大了(超過4個)就分裂)為例,依次刪除H,T,R,E。

1、首先刪除元素H,當然首先查詢H,H在一個葉子結點中,且該葉子結點元素數目3大於最小元素數目ceil(m/2)-1=2,則操作很簡單,咱們只需要移動K至原來H的位置,移動L至K的位置(也就是結點中刪除元素後面的元素向前移動)
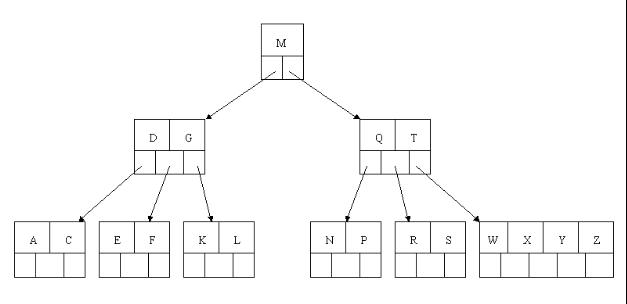
2、下一步,刪除T,因為T沒有在葉子結點中,而是在中間結點中找到,咱們發現他的繼承者W(字母升序的下個元素),將W上移到T的位置,然後將原包含W的孩子結點中的W進行刪除,這裡恰好刪除W後,該孩子結點中元素個數大於2,無需進行合併操作。
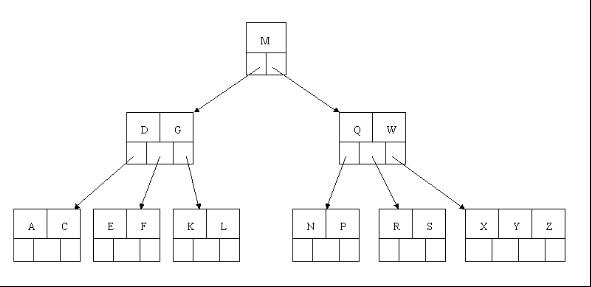
3、下一步刪除R,R在葉子結點中,但是該結點中元素數目為2,刪除導致只有1個元素,已經小於最小元素數目ceil(5/2)-1=2,而由前面我們已經知道:如果其某個相鄰兄弟結點中比較豐滿(元素個數大於ceil(5/2)-1=2),則可以向父結點借一個元素,然後將最豐滿的相鄰兄弟結點中上移最後或最前一個元素到父節點中(有沒有看到紅黑樹中左旋操作的影子?),在這個例項中,右相鄰兄弟結點中比較豐滿(3個元素大於2),所以先向父節點借一個元素W下移到該葉子結點中,代替原來S的位置,S前移;然後X在相鄰右兄弟結點中上移到父結點中,最後在相鄰右兄弟結點中刪除X,後面元素前移。
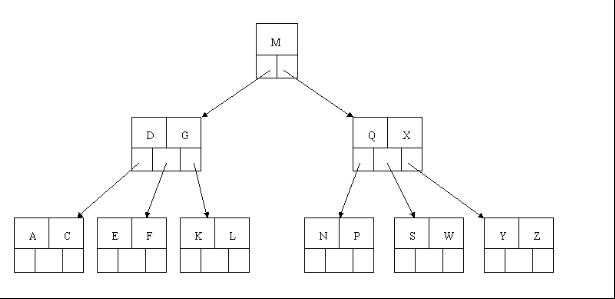
4、最後一步刪除E, 刪除後會導致很多問題,因為E所在的結點數目剛好達標,剛好滿足最小元素個數(ceil(5/2)-1=2),而相鄰的兄弟結點也是同樣的情況,刪除一個元素都不能滿足條件,所以需要該節點與某相鄰兄弟結點進行合併操作;首先移動父結點中的元素(該元素在兩個需要合併的兩個結點元素之間)下移到其子結點中,然後將這兩個結點進行合併成一個結點。所以在該例項中,咱們首先將父節點中的元素D下移到已經刪除E而只有F的結點中,然後將含有D和F的結點和含有A,C的相鄰兄弟結點進行合併成一個結點。
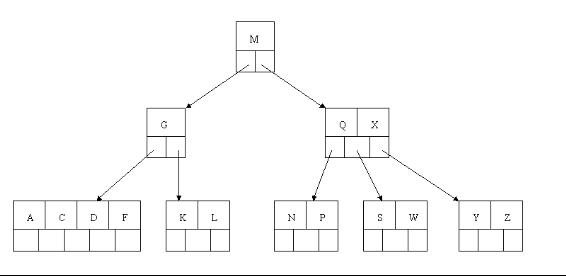
5、也許你認為這樣刪除操作已經結束了,其實不然,在看看上圖,對於這種特殊情況,你立即會發現父節點只包含一個元素G,沒達標(因為非根節點包括葉子結點的關鍵字數n必須滿足於2=<n<=4,而此處的n=1),這是不能夠接受的。如果這個問題結點的相鄰兄弟比較豐滿,則可以向父結點借一個元素。假設這時右兄弟結點(含有Q,X)有一個以上的元素(Q右邊還有元素),然後咱們將M下移到元素很少的子結點中,將Q上移到M的位置,這時,Q的左子樹將變成M的右子樹,也就是含有N,P結點被依附在M的右指標上。所以在這個例項中,咱們沒有辦法去借一個元素,只能與兄弟結點進行合併成一個結點,而根結點中的唯一元素M下移到子結點,這樣,樹的高度減少一層。

為了進一步詳細討論刪除的情況,再舉另外一個例項:
這裡是一棵不同的5序B樹,那咱們試著刪除C
於是將刪除元素C的右子結點中的D元素上移到C的位置,但是出現上移元素後,只有一個元素的結點的情況。
又因為含有E的結點,其相鄰兄弟結點才剛脫貧(最少元素個數為2),不可能向父節點借元素,所以只能進行合併操作,於是這裡將含有A,B的左兄弟結點和含有E的結點進行合併成一個結點。

這樣又出現只含有一個元素F結點的情況,這時,其相鄰的兄弟結點是豐滿的(元素個數為3>最小元素個數2),這樣就可以想父結點借元素了,把父結點中的J下移到該結點中,相應的如果結點中J後有元素則前移,然後相鄰兄弟結點中的第一個元素(或者最後一個元素)上移到父節點中,後面的元素(或者前面的元素)前移(或者後移);注意含有K,L的結點以前依附在M的左邊,現在變為依附在J的右邊。這樣每個結點都滿足B樹結構性質。
從以上操作可看出:除根結點之外的結點(包括葉子結點)的關鍵字的個數n滿足:(ceil(m / 2)-1)<= n <= m-1,即2<=n<=4。這也佐證了咱們之前的觀點。刪除操作完。
在B_樹中關鍵字分佈在整個B_樹,並且在上層結點中出現過的關鍵字不再出現在最底層的結點中。順序鏈中所有的關鍵字不能連線在一起。
一顆m階的B+樹和m階的B_樹的差異在於:
1.有n棵子樹的結點中含有n個關鍵字; (而B樹是n棵子樹有n-1個關鍵字)
2.所有的葉子結點中包含了全部關鍵字的資訊,及指向含有這些關鍵字記錄的指標,且葉子結點本身依關鍵字的大小自小而大的順序連結。(而B樹的葉子節點並沒有包括全部需要查詢的資訊)
3.所有的非終端結點可以看成是索引部分,結點中僅含有其子樹根結點中最大(或最小)關鍵字。 (而B 樹的非終節點也包含需要查詢的有效資訊)
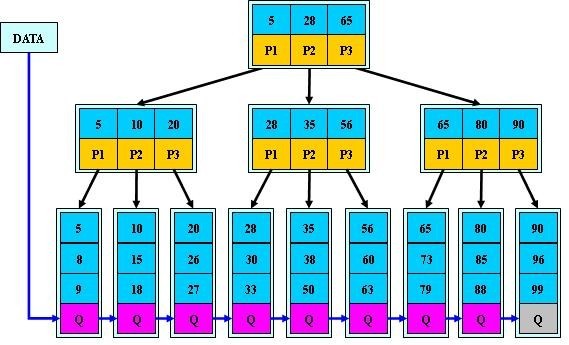
1) B+-tree的磁碟讀寫代價更低
B+-tree的內部結點並沒有指向關鍵字具體資訊的指標。因此其內部結點相對B 樹更小。如果把所有同一內部結點的關鍵字存放在同一盤塊中,那麼盤塊所能容納的關鍵字數量也越多。一次性讀入記憶體中的需要查詢的關鍵字也就越多。相對來說IO讀寫次數也就降低了。
舉個例子,假設磁碟中的一個盤塊容納16bytes,而一個關鍵字2bytes,一個關鍵字具體資訊指標2bytes。一棵9階B-tree(一個結點最多8個關鍵字)的內部結點需要2個盤快。而B+ 樹內部結點只需要1個盤快。當需要把內部結點讀入記憶體中的時候,B 樹就比B+ 樹多一次盤塊查詢時間(在磁碟中就是碟片旋轉的時間)。
2) B+-tree的查詢效率更加穩定
由於非終結點並不是最終指向檔案內容的結點,而只是葉子結點中關鍵字的索引。所以任何關鍵字的查詢必須走一條從根結點到葉子結點的路。所有關鍵字查詢的路徑長度相同,導致每一個數據的查詢效率相當。
相關推薦
BTree和B+Tree詳解
B 樹是為了磁碟或其它儲存裝置而設計的一種多叉(下面你會看到,相對於二叉,B樹每個內結點有多個分支,即多叉)平衡查詢樹。 B 樹又叫平衡多路查詢樹。一棵m階的B 樹 (m叉樹)的特性如下: 樹中每個結點最多含有m個孩子(m>=2); 除根結點和葉子結點外,
BTree和B+Tree和Hash索引詳解
b-tree 關系 查詢優化 刪除節點 eight node 常用 技術分享 遍歷 二叉查找樹 二叉樹具有以下性質:左子樹的鍵值小於根的鍵值,右子樹的鍵值大於根的鍵值。 如下圖所示就是一棵二叉查找樹, 對該二叉樹的節點進行查找發現深度為1的節點的查找次數為1,深度為2的查
BTree和B+Tree
B+樹索引是B+樹在資料庫中的一種實現,是最常見也是資料庫中使用最為頻繁的一種索引。B+樹中的B代表平衡(balance),而不是二叉(binary),因為B+樹是從最早的平衡二叉樹演化而來的。在講B+樹之前必須先了解二叉查詢樹、平衡二叉樹(AVLTree)和平
關於索引的B tree B-tree B+tree B*tree 詳解結構圖
B樹 即二叉搜尋樹: 1.所有非葉子結點至多擁有兩個兒子(Left和Right); 2.所有結點儲存一個關鍵字; 3.非葉子結點的左指標指向小於其關鍵字的子樹,右指標指向大於其關鍵字的子樹; 如: B樹的搜尋,從根結點開始,如果查詢的關鍵字與結點的
B-tree詳解及實現(C語言)
// // MBTree.c // MBTree // // Created by Wuyixin on 2017/8/4. // Copyright © 2017年 Coding365. All rights reserved. // #include "MBTree.h" static K
B+tree詳解及實現(C語言)
// // BPlusTree.c // BPlusTree // // Created by Wuyixin on 2017/8/4. // Copyright © 2017年 Coding365. All rights reserved. // #include "BPlusTree.h"
關於索引的B tree B-tree B+tree B*tree 詳解結構圖( 二)
索引,是為了更快的查詢資料,查詢演算法有很多,對應的資料結構也不少,資料庫常用的索引資料結構一般為B+Tree。 1、B-Tree 關於B-Tree的官方定義個人覺得比較難懂,通俗一點就是舉個例子。假如:一本英文字典,單詞+詳細解釋組成了一條記錄,現在需要索引單詞,那麼以單詞為key,單詞+詳細解釋為
MySQL索引原理及BTree(B-/+Tree)結構詳解
目錄 摘要 資料結構及演算法基礎 索引的本質 B-Tree和B+Tree B-Tree B+Tree 帶有順序訪問指標的B+Tree 為什麼使用B-Tree(B+Tree) 主存存取原理 磁碟存取原理 區域性性原理與磁碟預讀 B
轉載 logback的使用和logback.xml詳解 http://www.cnblogs.com/warking/p/5710303.html
version tor red java代碼 根節點 ext private 字符串 npe logback的使用和logback.xml詳解 一、logback的介紹 Logback是由log4j創始人設計的另一個開源日誌組件,官方網站: http://logb
微信公眾開發URL和token填寫詳解
res wrap this true 進行 -m tmp sem 知識 微信公眾開發URL和token填寫詳解 方法/步驟 作為一名微信公眾號開發者,別人進入你的微信公眾號,肯定會看見某些網頁,或者給你發某些信息,你需要實時自動回復,所以你
storm集群部署和配置過程詳解
多少 帶來 進程 創建 使用 命令 介紹 aml 可能 ---恢復內容開始--- 先整體介紹一下搭建storm集群的步驟: 設置zookeeper集群 安裝依賴到所有nimbus和worker節點 下載並解壓storm發布版本到所有nimbus和worker節點 配置s
接口測試工具soapUI的安裝和使用方法詳解
service 技術 key custom media 負載 bmp file text soapUI是一個開源測試工具,通過soap/http來檢查、調用、實現Web Service的功能/負載/符合性測試。 使用soapUI可以非常方便的實現接口的功能測試、穩
Sql Server參數化查詢之where in和like實現詳解
blog charindex 語句 pan 建議 ack rop for 臨時表 文章導讀 拼SQL實現where in查詢 使用CHARINDEX或like實現where in 參數化 使用exec動態執行SQl實現where in 參數化 為每一個參數生成一個參數
MySQL存儲引擎中的MyISAM和InnoDB區別詳解
訪問 過程 包含 lte 處理機制 comm 用戶 isam log MyISAM是MySQL的默認數據庫引擎(5.5版之前),由早期的ISAM(Indexed Sequential Access Method:有索引的順序訪問方法)所改良。雖然性能極佳,但卻有一個缺點:不
Android Studio中Git和GitHub使用詳解
可能 必須 窗口 gin 擁有 說明 詳細 對話 發現 一、Git和GitHub簡述 1.Git 分布式版本控制系統,最先使用於Linux社區,是一個開源免費的版本控制系統,功能類似於SVN和CVS。Git與其他版本管理工具最大的區別點和優點就是分布式;
MyISAM和InnoDB區別詳解
sam 是什麽 註意 高速 dump 在操作 必須 index 自己 MyISAM是MySQL的默認數據庫引擎(5.5版之前),由早期的ISAM(Indexed Sequential Access Method:有索引的順序訪問方法)所改良。雖然性能極佳,但卻有一個缺點:不
netstat Recv-Q和Send-Q詳解
java ket -a ant 相關 csdn min any ber http://blog.csdn.net/sjin_1314/article/details/9853163 通過netstat -anp可以查看機器的當前連接狀態: Active Inter
js keyup、keypress和keydown事件 詳解
rgs spa 小鍵盤 ansi 使用方法 form 單個 sage ges js keyup、keypress和keydown事件都是有關於鍵盤的事件 當一個按鍵被pressed 或released在每一個現代瀏覽器中,都可能有三種客戶端事件。 keydown even
NFS服務器原理和安裝配置詳解附案例演練
隨機選擇 span 通訊 操作系統 不同 網絡 定義 重新啟動 exportfs NFS服務器原理和安裝配置詳解附案例演練 1、什麽是NFS服務器 NFS就是Network File System的縮寫,它最大的功能就是可以通過網絡,讓不同的機器、不同的操作系統可以共享
轉:logback的使用和logback.xml詳解
靈活 多說 maven path socket win error 輸出日誌 功能 一、logback的介紹 Logback是由log4j創始人設計的另一個開源日誌組件,官方網站: http://logback.qos.ch。它當前分為下面下個模塊: logback-c
