用度定義的B樹

      針對上面的5點，再闡述下：B樹中每一個結點能包含的關鍵字（如之前上面的D H和Q T X）數有一個上界和下界。這個下界可以用一個稱作B樹的最小度數（演算法導論中文版上譯作度數，最小度數即內節點中節點最小孩子數目）m（m>=2）表示。

• 每個非根的內結點至多有m個子女，每個非根的結點必須至少含有m-1個關鍵字，如果樹是非空的，則根結點至少包含一個關鍵字；
• 每個結點可包含至多2m-1個關鍵字。所以一個內結點至多可有2m個子女。如果一個結點恰好有2m-1個關鍵字，我們就說這個結點是滿的（而稍後介紹的B*樹作為B樹的一種常用變形，B*樹中要求每個內結點至少為2/3滿，而不是像這裡的B樹所要求的至少半滿
  ）；
• 當關鍵字數m=2（t=2的意思是，mmin=2，m可以>=2）時的B樹是最簡單的（有很多人會因此誤認為B樹就是二叉查詢樹，但二叉查詢樹就是二叉查詢樹，B樹就是B樹，B樹是一棵含有m（m>=2）個關鍵字的平衡多路查詢樹），此時，每個內結點可能因此而含有2個、3個或4個子女，亦即一棵2-3-4樹，然而在實際中，通常採用大得多的t值。

    B樹中的每個結點根據實際情況可以包含大量的關鍵字資訊和分支(當然是不能超過磁碟塊的大小，根據磁碟驅動(disk drives)的不同，一般塊的大小在1k~4k左右)；這樣樹的深度降低了，這就意味著查詢一個元素只要很少結點從外存磁碟中讀入記憶體，很快訪問到要查詢的資料。如果你看完上面關於B樹定義的介紹，思維感覺不夠清晰，請繼續參閱下文第

6小節、B樹的插入、刪除操作 部分。

    3.2B樹的型別和節點定義

    B樹的型別和節點定義如下圖所示：

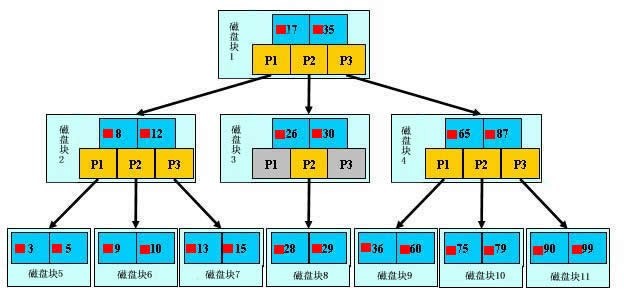
    3.3檔案查詢的具體過程(涉及磁碟IO操作)

為了簡單，這裡用少量資料構造一棵3叉樹的形式，實際應用中的B樹結點中關鍵字很多的。上面的圖中比如根結點，其中17表示一個磁碟檔案的檔名；小紅方塊表示這個17檔案內容在硬碟中的儲存位置；p1表示指向17左子樹的指標。

其結構可以簡單定義為：

typedef struct {

    /*檔案數*/

    int  file_num;

    /*檔名(key)*/

    char * file_name[max_file_num];

    /*指向子節點的指標*/

     BTNode * BTptr[max_file_num+1];

     /*檔案在硬碟中的儲存位置*/

     FILE_HARD_ADDR offset[max_file_num];

}BTNode;

假如每個盤塊可以正好存放一個B樹的結點（正好存放2個檔名）。那麼一個BTNODE結點就代表一個盤塊，而子樹指標就是存放另外一個盤塊的地址。

下面，咱們來模擬下查詢檔案29的過程：

1. 根據根結點指標找到檔案目錄的根磁碟塊1，將其中的資訊匯入記憶體。【磁碟IO操作 1次】
2. 此時記憶體中有兩個檔名17、35和三個儲存其他磁碟頁面地址的資料。根據演算法我們發現：17<29<35，因此我們找到指標p2。
3. 根據p2指標，我們定位到磁碟塊3，並將其中的資訊匯入記憶體。【磁碟IO操作 2次】
4. 此時記憶體中有兩個檔名26，30和三個儲存其他磁碟頁面地址的資料。根據演算法我們發現：26<29<30，因此我們找到指標p2。
5. 根據p2指標，我們定位到磁碟塊8，並將其中的資訊匯入記憶體。【磁碟IO操作 3次】
6. 此時記憶體中有兩個檔名28，29。根據演算法我們查詢到檔名29，並定位了該檔案記憶體的磁碟地址。

分析上面的過程，發現需要3次磁碟IO操作和3次記憶體查詢操作。關於記憶體中的檔名查詢，由於是一個有序表結構，可以利用折半查詢提高效率。至於IO操作是影響整個B樹查詢效率的決定因素。

當然，如果我們使用平衡二叉樹的磁碟儲存結構來進行查詢，磁碟4次，最多5次，而且檔案越多，B樹比平衡二叉樹所用的磁碟IO操作次數將越少，效率也越高。

3.4B樹的高度

    根據上面的例子我們可以看出，對於輔存做IO讀的次數取決於B樹的高度。而B樹的高度由什麼決定的呢？

    若B樹某一非葉子節點包含N個關鍵字，則此非葉子節點含有N+1個孩子結點，而所有的葉子結點都在第I層，我們可以得出：

1. 因為根至少有兩個孩子，因此第2層至少有兩個結點。
2. 除根和葉子外，其它結點至少有┌m/2┐個孩子，
3. 因此在第3層至少有2*┌m/2┐個結點，
4. 在第4層至少有2*(┌m/2┐^2)個結點，
5. 在第 I 層至少有2*(┌m/2┐^(l-2) )個結點，於是有： N+1 ≥ 2*┌m/2┐I-2；
6. 考慮第L層的結點個數為N+1，那麼2*(┌m/2┐^(l-2)）≤N+1，也就是L層的最少結點數剛好達到N+1個，即： I≤ log┌m/2┐((N+1)/2 )+2；

　　所以

• 當B樹包含N個關鍵字時，B樹的最大高度為l-1（因為計算B樹高度時，葉結點所在層不計算在內），即：l - 1 = log┌m/2┐((N+1)/2 )+1。

　　這個B樹的高度公式從側面顯示了B樹的查詢效率是相當高的。 曾在一次面試中被問到，一棵含有N個總關鍵字數的m階的B樹的最大高度是多少?答曰：log_ceil（m/2）(N+1)/2 + 1 （上面中關於m階B樹的第1點特性已經提到：樹中每個結點含有最多含有m個孩子，即m滿足：ceil(m/2)<=m<=m。而樹中每個結點含孩子數越少，樹的高度則越大，故如此）。在2012微軟4月份的筆試中也問到了此問題。
此外，還有讀者反饋，說上面的B樹的高度計算公式與演算法導論一書上的不同，而後我特意翻看了演算法導論第18章關於B樹的高度一節的內容，如下圖所示： 在上圖中書上所舉的例子中，也許，根據我們大多數人的理解，它的高度應該是4，而書上卻說的是“一棵高度為3的B樹”。我想，此時，你也就明白了，演算法導論一書上的高度的定義是從“0”開始計數的，而我們中國人的習慣是樹的高度是從“1”開始計數的。特此說明。July、二零一二年九月二十七日。

B⁺-tree：是應檔案系統所需而產生的一種B-tree的變形樹。

一棵m階的B+樹和m階的B樹的異同點在於：

      1.有n棵子樹的結點中含有n-1 個關鍵字； (此處頗有爭議，B+樹到底是與B 樹n棵子樹有n-1個關鍵字 保持一致，還是不一致：B樹n棵子樹的結點中含有n個關鍵字，待後續查證。暫先提供兩個參考連結：①wikipedia http://en.wikipedia.org/wiki/B%2B_tree#Overview；②http://hedengcheng.com/?p=525。而下面B+樹的圖尚未最終確定是否有問題，請讀者注意)

      2.所有的葉子結點中包含了全部關鍵字的資訊，及指向含有這些關鍵字記錄的指標，且葉子結點本身依關鍵字的大小自小而大的順序連結。 (而B 樹的葉子節點並沒有包括全部需要查詢的資訊)

      3.所有的非終端結點可以看成是索引部分，結點中僅含有其子樹根結點中最大（或最小）關鍵字。 (而B 樹的非終節點也包含需要查詢的有效資訊)

 

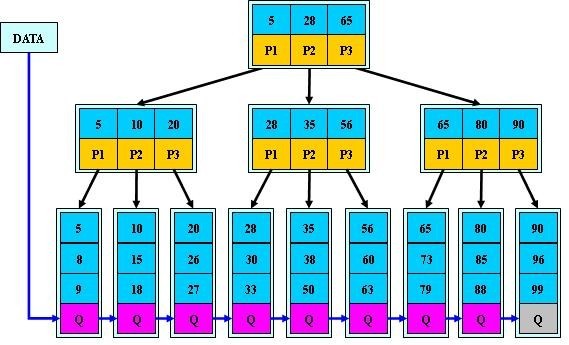
a)     為什麼說B⁺-tree比B 樹更適合實際應用中作業系統的檔案索引和資料庫索引？

1) B⁺-tree的磁碟讀寫代價更低

B⁺-tree的內部結點並沒有指向關鍵字具體資訊的指標。因此其內部結點相對B 樹更小。如果把所有同一內部結點的關鍵字存放在同一盤塊中，那麼盤塊所能容納的關鍵字數量也越多。一次性讀入記憶體中的需要查詢的關鍵字也就越多。相對來說IO讀寫次數也就降低了。

舉個例子，假設磁碟中的一個盤塊容納16bytes，而一個關鍵字2bytes，一個關鍵字具體資訊指標2bytes。一棵9階B-tree(一個結點最多8個關鍵字)的內部結點需要2個盤快。而B⁺ 樹內部結點只需要1個盤快。當需要把內部結點讀入記憶體中的時候，B 樹就比B⁺ 樹多一次盤塊查詢時間(在磁碟中就是碟片旋轉的時間)。

2) B⁺-tree的查詢效率更加穩定

由於非終結點並不是最終指向檔案內容的結點，而只是葉子結點中關鍵字的索引。所以任何關鍵字的查詢必須走一條從根結點到葉子結點的路。所有關鍵字查詢的路徑長度相同，導致每一個數據的查詢效率相當。

讀者點評
本文評論下第149樓，fanyy1991針對上文所說的兩點，道：個人覺得這兩個原因都不是主要原因。資料庫索引採用B+樹的主要原因是 B樹在提高了磁碟IO效能的同時並沒有解決元素遍歷的效率低下的問題。正是為了解決這個問題，B+樹應運而生。B+樹只要遍歷葉子節點就可以實現整棵樹的遍歷。而且在資料庫中基於範圍的查詢是非常頻繁的，而B樹不支援這樣的操作（或者說效率太低）。

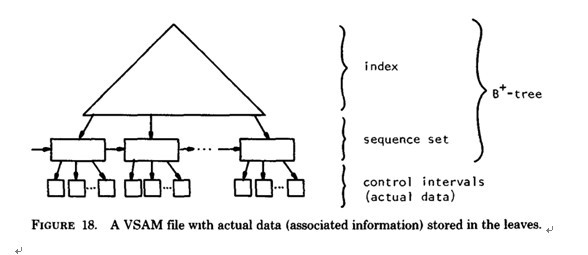
b)    B⁺-tree的應用: VSAM(虛擬儲存存取法)檔案(來源論文 the ubiquitous Btree 作者：D COMER - 1979 )

 

5.B^*-tree

B*-tree是B⁺-tree的變體，在B⁺樹的基礎上(所有的葉子結點中包含了全部關鍵字的資訊，及指向含有這些關鍵字記錄的指標)，B*樹中非根和非葉子結點再增加指向兄弟的指標；B*樹定義了非葉子結點關鍵字個數至少為(2/3)*M，即塊的最低使用率為2/3（代替B+樹的1/2）。給出了一個簡單例項，如下圖所示：

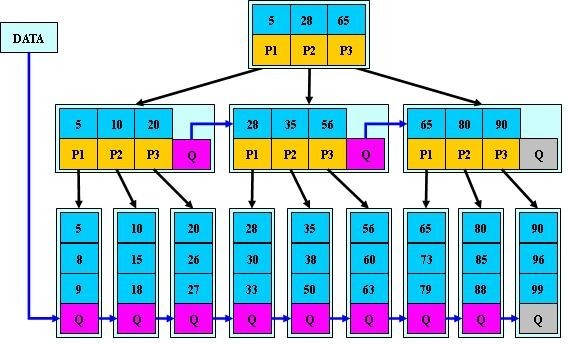
B+樹的分裂：當一個結點滿時，分配一個新的結點，並將原結點中1/2的資料複製到新結點，最後在父結點中增加新結點的指標；B+樹的分裂隻影響原結點和父結點，而不會影響兄弟結點，所以它不需要指向兄弟的指標。

B*樹的分裂：當一個結點滿時，如果它的下一個兄弟結點未滿，那麼將一部分資料移到兄弟結點中，再在原結點插入關鍵字，最後修改父結點中兄弟結點的關鍵字（因為兄弟結點的關鍵字範圍改變了）；如果兄弟也滿了，則在原結點與兄弟結點之間增加新結點，並各複製1/3的資料到新結點，最後在父結點增加新結點的指標。

所以，B*樹分配新結點的概率比B+樹要低，空間使用率更高；

6、B樹的插入、刪除操作

上面第3小節簡單介紹了利用B樹這種結構如何訪問外存磁碟中的資料的情況，下面咱們通過另外一個例項來對這棵B樹的插入（insert）,刪除（delete）基本操作進行詳細的介紹。 但在此之前，咱們還得簡單回顧下一棵m階的B 樹的特性，如下：

1. 樹中每個結點含有最多含有m個孩子，即m滿足：ceil(m/2)<=m<=m。
2. 除根結點和葉子結點外，其它每個結點至少有[ceil(m / 2)]個孩子（其中ceil(x)是一個取上限的函式）；
3. 若根結點不是葉子結點，則至少有2個孩子（特殊情況：沒有孩子的根結點，即根結點為葉子結點，整棵樹只有一個根節點）；
4. 所有葉子結點都出現在同一層，葉子結點不包含任何關鍵字資訊(可以看做是外部接點或查詢失敗的接點，實際上這些結點不存在，指向這些結點的指標都為null)；
5. 每個非終端結點中包含有n個關鍵字資訊： (n，P0，K1，P1，K2，P2，......，Kn，Pn)。其中：
          a)   Ki (i=1...n)為關鍵字，且關鍵字按順序升序排序K(i-1)< Ki。 
          b)   Pi為指向子樹根的接點，且指標P(i-1)指向子樹種所有結點的關鍵字均小於Ki，但都大於K(i-1)。 
          c)   除根結點之外的結點的關鍵字的個數n必須滿足： [ceil(m / 2)-1]<= n <= m-1（葉子結點也必須滿足此條關於關鍵字數的性質，根結點除外）。

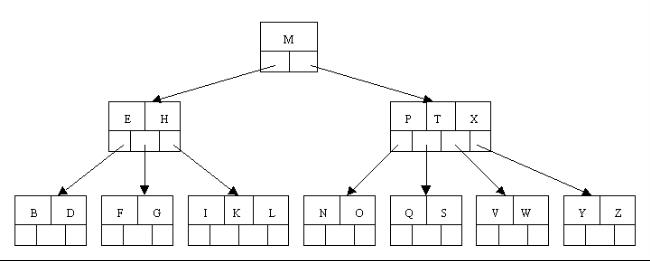
ok，下面咱們以一棵5階（即樹中任一結點至多含有4個關鍵字，5棵子樹）B樹例項進行講解(如下圖所示)：

備註：關鍵字數（2-4個）針對--非根結點（包括葉子結點在內），孩子數（3-5個）--針對根結點和葉子結點之外的內結點。當然，根結點是必須至少有2個孩子的，不然就成直線型搜尋樹了。下圖中，讀者可以看到關鍵字數2-4個，內結點孩子數3-5個：

關鍵字為大寫字母，順序為字母升序。

結點定義如下：

typedef struct{

   int Count;         // 當前節點中關鍵元素數目

   ItemType Key[4];   // 儲存關鍵字元素的陣列

   long Branch[5];    // 偽指標陣列，(記錄數目)方便判斷合併和分裂的情況

} NodeType;

6.1、插入（insert）操作

插入一個元素時，首先在B樹中是否存在，如果不存在，即在葉子結點處結束，然後在葉子結點中插入該新的元素，注意：如果葉子結點空間足夠，這裡需要向右移動該葉子結點中大於新插入關鍵字的元素，如果空間滿了以致沒有足夠的空間去新增新的元素，則將該結點進行“分裂”，將一半數量的關鍵字元素分裂到新的其相鄰右結點中，中間關鍵字元素上移到父結點中（當然，如果父結點空間滿了，也同樣需要“分裂”操作），而且當結點中關鍵元素向右移動了，相關的指標也需要向右移。如果在根結點插入新元素，空間滿了，則進行分裂操作，這樣原來的根結點中的中間關鍵字元素向上移動到新的根結點中，因此導致樹的高度增加一層。如下圖所示：

1、OK，下面咱們通過一個例項來逐步講解下。插入以下字元字母到一棵空的B 樹中（非根結點關鍵字數小了（小於2個）就合併，大了（超過4個）就分裂）：C N G A H E K Q M F W L T Z D P R X Y S，首先，結點空間足夠，4個字母插入相同的結點中，如下圖：

2、當咱們試著插入H時，結點發現空間不夠，以致將其分裂成2個結點，移動中間元素G上移到新的根結點中，在實現過程中，咱們把A和C留在當前結點中，而H和N放置新的其右鄰居結點中。如下圖：

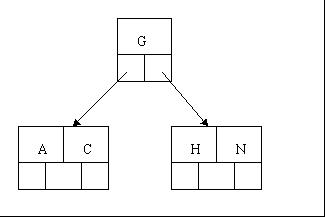
3、當咱們插入E,K,Q時，不需要任何分裂操作

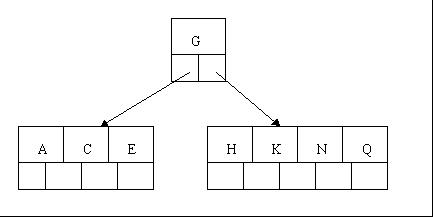
4、插入M需要一次分裂，注意M恰好是中間關鍵字元素，以致向上移到父節點中

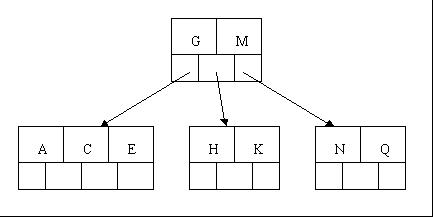
5、插入F,W,L,T不需要任何分裂操作

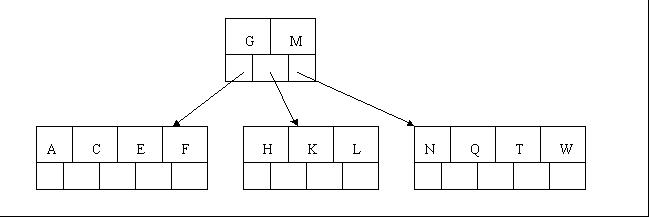
6、插入Z時，最右的葉子結點空間滿了，需要進行分裂操作，中間元素T上移到父節點中，注意通過上移中間元素，樹最終還是保持平衡，分裂結果的結點存在2個關鍵字元素。

7、插入D時，導致最左邊的葉子結點被分裂，D恰好也是中間元素，上移到父節點中，然後字母P,R,X,Y陸續插入不需要任何分裂操作（別忘了，樹中至多5個孩子）。

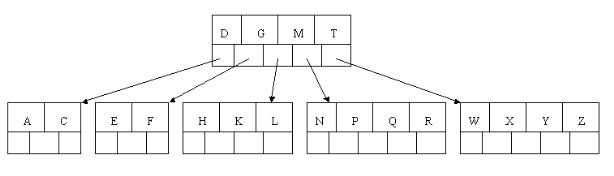
8、最後，當插入S時，含有N,P,Q,R的結點需要分裂，把中間元素Q上移到父節點中，但是情況來了，父節點中空間已經滿了，所以也要進行分裂，將父節點中的中間元素M上移到新形成的根結點中，注意以前在父節點中的第三個指標在修改後包括D和G節點中。這樣具體插入操作的完成，下面介紹刪除操作，刪除操作相對於插入操作要考慮的情況多點。

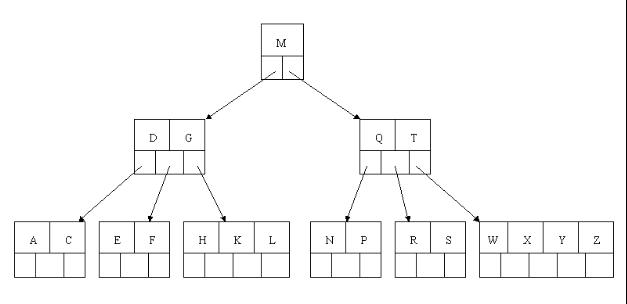
6.2、刪除(delete)操作

首先查詢B樹中需刪除的元素,如果該元素在B樹中存在，則將該元素在其結點中進行刪除，如果刪除該元素後，首先判斷該元素是否有左右孩子結點，如果有，則上移孩子結點中的某相近元素(“左孩子最右邊的節點”或“右孩子最左邊的節點”)到父節點中，然後是移動之後的情況；如果沒有，直接刪除後，移動之後的情況。

刪除元素，移動相應元素之後，如果某結點中元素數目（即關鍵字數）小於ceil(m/2)-1，則需要看其某相鄰兄弟結點是否豐滿（結點中元素個數大於ceil(m/2)-1）（還記得第一節中關於B樹的第5個特性中的c點麼?： c)除根結點之外的結點（包括葉子結點）的關鍵字的個數n必須滿足： （ceil(m / 2)-1）<= n <= m-1。m表示最多含有m個孩子，n表示關鍵字數。在本小節中舉的一顆B樹的示例中，關鍵字數n滿足：2<=n<=4），如果豐滿，則向父節點借一個元素來滿足條件；如果其相鄰兄弟都剛脫貧，即借了之後其結點數目小於ceil(m/2)-1，則該結點與其相鄰的某一兄弟結點進行“合併”成一個結點，以此來滿足條件。那咱們通過下面例項來詳細瞭解吧。

以上述插入操作構造的一棵5階B樹（樹中最多含有m（m=5）個孩子，因此關鍵字數最小為ceil(m / 2)-1=2。還是這句話，關鍵字數小了（小於2個）就合併，大了（超過4個）就分裂）為例，依次刪除H,T,R,E。

1、首先刪除元素H，當然首先查詢H，H在一個葉子結點中，且該葉子結點元素數目3大於最小元素數目ceil(m/2)-1=2，則操作很簡單，咱們只需要移動K至原來H的位置，移動L至K的位置（也就是結點中刪除元素後面的元素向前移動）

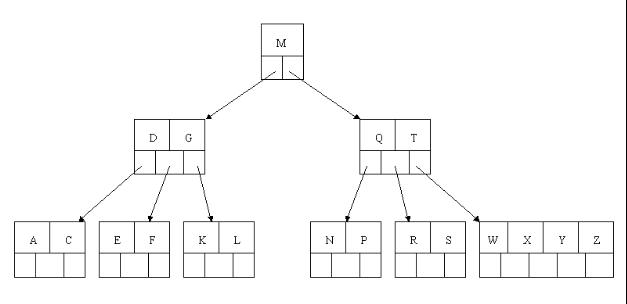
2、下一步，刪除T,因為T沒有在葉子結點中，而是在中間結點中找到，咱們發現他的繼承者W(字母升序的下個元素)，將W上移到T的位置，然後將原包含W的孩子結點中的W進行刪除，這裡恰好刪除W後，該孩子結點中元素個數大於2，無需進行合併操作。

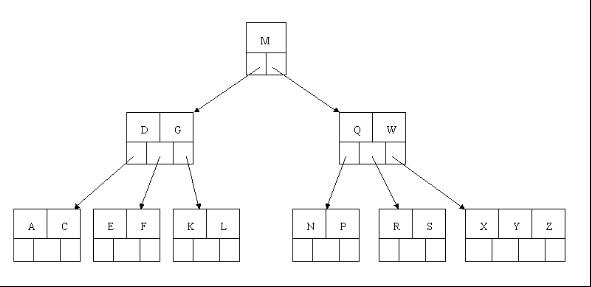
3、下一步刪除R，R在葉子結點中,但是該結點中元素數目為2，刪除導致只有1個元素，已經小於最小元素數目ceil(5/2)-1=2,而由前面我們已經知道：如果其某個相鄰兄弟結點中比較豐滿（元素個數大於ceil(5/2)-1=2），則可以向父結點借一個元素，然後將最豐滿的相鄰兄弟結點中上移最後或最前一個元素到父節點中（有沒有看到紅黑樹中左旋操作的影子?），在這個例項中，右相鄰兄弟結點中比較豐滿（3個元素大於2），所以先向父節點借一個元素W下移到該葉子結點中，代替原來S的位置，S前移；然後X在相鄰右兄弟結點中上移到父結點中，最後在相鄰右兄弟結點中刪除X，後面元素前移。

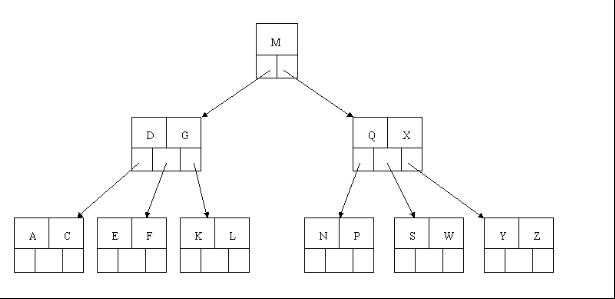
4、最後一步刪除E， 刪除後會導致很多問題，因為E所在的結點數目剛好達標，剛好滿足最小元素個數（ceil(5/2)-1=2）,而相鄰的兄弟結點也是同樣的情況，刪除一個元素都不能滿足條件，所以需要該節點與某相鄰兄弟結點進行合併操作；首先移動父結點中的元素（該元素在兩個需要合併的兩個結點元素之間）下移到其子結點中，然後將這兩個結點進行合併成一個結點。所以在該例項中，咱們首先將父節點中的元素D下移到已經刪除E而只有F的結點中，然後將含有D和F的結點和含有A,C的相鄰兄弟結點進行合併成一個結點。

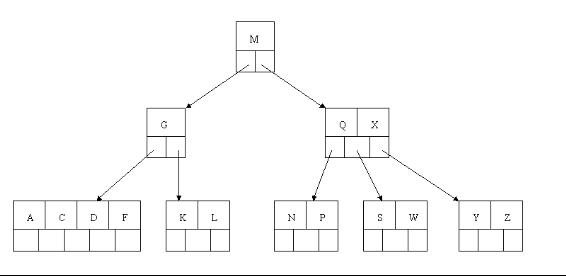
5、也許你認為這樣刪除操作已經結束了，其實不然，在看看上圖，對於這種特殊情況，你立即會發現父節點只包含一個元素G，沒達標（因為非根節點包括葉子結點的關鍵字數n必須滿足於2=<n<=4，而此處的n=1），這是不能夠接受的。如果這個問題結點的相鄰兄弟比較豐滿，則可以向父結點借一個元素。假設這時右兄弟結點（含有Q,X）有一個以上的元素（Q右邊還有元素），然後咱們將M下移到元素很少的子結點中，將Q上移到M的位置，這時，Q的左子樹將變成M的右子樹，也就是含有N，P結點被依附在M的右指標上。所以在這個例項中，咱們沒有辦法去借一個元素，只能與兄弟結點進行合併成一個結點，而根結點中的唯一元素M下移到子結點，這樣，樹的高度減少一層。

為了進一步詳細討論刪除的情況，再舉另外一個例項：

這裡是一棵不同的5序B樹，那咱們試著刪除C

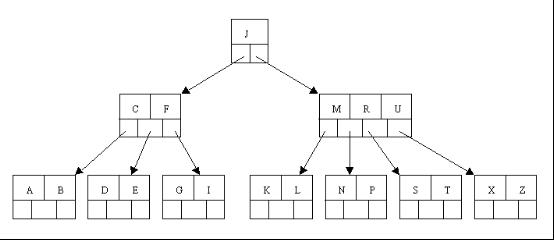
於是將刪除元素C的右子結點中的D元素上移到C的位置，但是出現上移元素後，只有一個元素的結點的情況。

又因為含有E的結點，其相鄰兄弟結點才剛脫貧（最少元素個數為2），不可能向父節點借元素，所以只能進行合併操作，於是這裡將含有A,B的左兄弟結點和含有E的結點進行合併成一個結點。

這樣又出現只含有一個元素F結點的情況，這時，其相鄰的兄弟結點是豐滿的（元素個數為3>最小元素個數2），這樣就可以想父結點借元素了，把父結點中的J下移到該結點中，相應的如果結點中J後有元素則前移，然後相鄰兄弟結點中的第一個元素（或者最後一個元素）上移到父節點中，後面的元素（或者前面的元素）前移（或者後移）；注意含有K，L的結點以前依附在M的左邊，現在變為依附在J的右邊。這樣每個結點都滿足B樹結構性質。

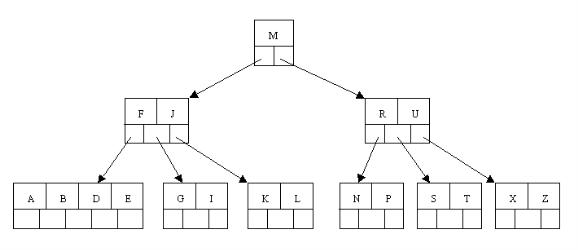
從以上操作可看出：除根結點之外的結點（包括葉子結點）的關鍵字的個數n滿足：（ceil(m / 2)-1）<= n <= m-1，即2<=n<=4。這也佐證了咱們之前的觀點。刪除操作完。

7.總結

通過以上介紹，大致將B樹，B+樹，B*樹總結如下：

B樹：有序陣列+平衡多叉樹；

B+樹：有序陣列連結串列+平衡多叉樹；

B*樹：一棵豐滿的B+樹。

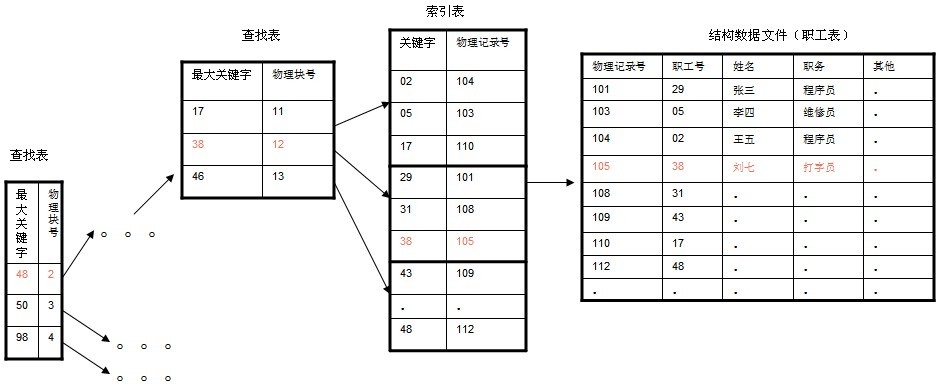
在大規模資料儲存的檔案系統中，B~tree系列資料結構，起著很重要的作用，對於儲存不同的資料，節點相關的資訊也是有所不同，這裡根據自己的理解，畫的一個查詢以職工號為關鍵字，職工號為38的記錄的簡單示意圖。(這裡假設每個物理塊容納3個索引，磁碟的I/O操作的基本單位是塊（block),磁碟訪問很費時，採用B+樹有效的減少了訪問磁碟的次數。）

對於像MySQL，DB2，Oracle等資料庫中的索引結構得有較深入的瞭解才行，建議去找一些B 樹相關的開原始碼研究。

走進搜尋引擎的作者樑斌老師針對B樹、B+樹給出了他的意見（為了真實性，特引用其原話，未作任何改動）： “B+樹還有一個最大的好處，方便掃庫，B樹必須用中序遍歷的方法按序掃庫，而B+樹直接從葉子結點挨個掃一遍就完了，B+樹支援range-query非常方便，而B樹不支援。這是資料庫選用B+樹的最主要原因。

    比如要查 5-10之間的，B+樹一把到5這個標記，再一把到10，然後串起來就行了，B樹就非常麻煩。B樹的好處，就是成功查詢特別有利，因為樹的高度總體要比B+樹矮。不成功的情況下，B樹也比B+樹稍稍佔一點點便宜。

    B樹比如你的例子中查，17的話，一把就得到結果了，
有很多基於頻率的搜尋是選用B樹，越頻繁query的結點越往根上走，前提是需要對query做統計，而且要對key做一些變化。

    另外B樹也好B+樹也好，根或者上面幾層因為被反覆query，所以這幾塊基本都在記憶體中，不會出現讀磁碟IO，一般已啟動的時候，就會主動換入記憶體。”非常感謝。

    Bucket Li："mysql 底層儲存是用B+樹實現的，知道為什麼麼。記憶體中B+樹是沒有優勢的，但是一到磁碟，B+樹的威力就出來了"。

第二節、R樹：處理空間儲存問題

相信經過上面第一節的介紹，你已經對B樹或者B+樹有所瞭解。這種樹可以非常好的處理一維空間儲存的問題。B樹是一棵平衡樹，它是把一維直線分為若干段線段，當我們查詢滿足某個要求的點的時候，只要去查詢它所屬的線段即可。依我看來，這種思想其實就是先找一個大的空間，再逐步縮小所要查詢的空間，最終在一個自己設定的最小不可分空間內找出滿足要求的解。一個典型的B樹查詢如下：

 

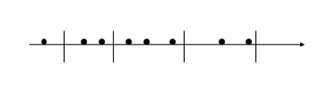
要查詢某一滿足條件的點，先去找到滿足條件的線段，然後遍歷所線上段上的點，即可找到答案。

B樹是一種相對來說比較複雜的資料結構，尤其是在它的刪除與插入操作過程中，因為它涉及到了葉子結點的分解與合併。由於本文第一節已經詳細介紹了B樹和B+樹，下面直接開始介紹我們的第二個主角：R樹。

簡介

1984年，加州大學伯克利分校的Guttman發表了一篇題為“R-trees: a dynamic index structure for spatial searching”的論文，向世人介紹了R樹這種處理高維空間儲存問題的資料結構。本文便是基於這篇論文寫作完成的，因此如果大家對R樹非常有興趣，我想最好還是參考一下原著：）。為表示對這位牛人的尊重，給個引用先：

Guttman, A.; “R-trees: a dynamic index structure for spatial searching,” ACM, 1984, 14

R樹在資料庫等領域做出的功績是非常顯著的。它很好的解決了在高維空間搜尋等問題。舉個R樹在現實領域中能夠解決的例子：查詢20英里以內所有的餐廳。如果沒有R樹你會怎麼解決？一般情況下我們會把餐廳的座標(x,y)分為兩個欄位存放在資料庫中，一個欄位記錄經度，另一個欄位記錄緯度。這樣的話我們就需要遍歷所有的餐廳獲取其位置資訊，然後計算是否滿足要求。如果一個地區有100家餐廳的話，我們就要進行100次位置計算操作了，如果應用到谷歌地圖這種超大資料庫中，這種方法便必定不可行了。

R樹就很好的解決了這種高維空間搜尋問題。它把B樹的思想很好的擴充套件到了多維空間，採用了B樹分割空間的思想，並在新增、刪除操作時採用合併、分解結點的方法，保證樹的平衡性。因此，R樹就是一棵用來儲存高維資料的平衡樹。

OK，接下來，本文將詳細介紹R樹的資料結構以及R樹的操作。至於R樹的擴充套件與R樹的效能問題，可以查閱相關論文。

R樹的資料結構

如上所述，R樹是B樹在高維空間的擴充套件，是一棵平衡樹。每個R樹的葉子結點包含了多個指向不同資料的指標，這些資料可以是存放在硬碟中的，也可以是存在記憶體中。根據R樹的這種資料結構，當我們需要進行一個高維空間查詢時，我們只需要遍歷少數幾個葉子結點所包含的指標，檢視這些指標指向的資料是否滿足要求即可。這種方式使我們不必遍歷所有資料即可獲得答案，效率顯著提高。下圖1是R樹的一個簡單例項：

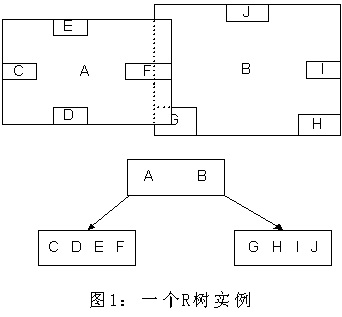
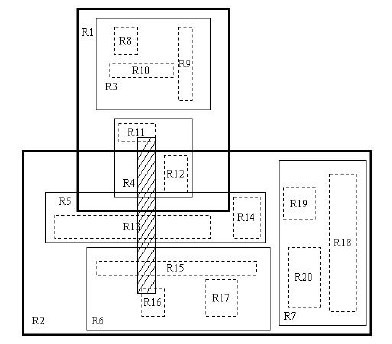
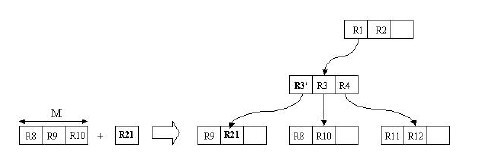
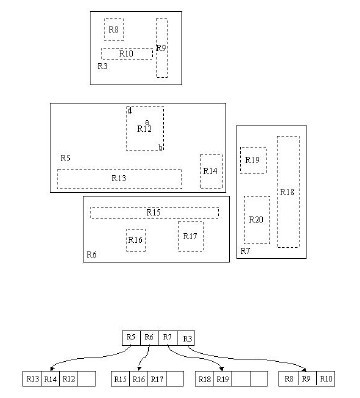
我們在上面說過，R樹運用了空間分割的理念，這種理念是如何實現的呢？R樹採用了一種稱為MBR(Minimal Bounding Rectangle)的方法，在此我把它譯作“最小邊界矩形”。從葉子結點開始用矩形（rectangle）將空間框起來，結點越往上，框住的空間就越大，以此對空間進行分割。有點不懂？沒關係，繼續往下看。在這裡我還想提一下，R樹中的R應該代表的是Rectangle（此處參考wikipedia上關於R樹的介紹），而不是大多數國內教材中所說的Region（很多書把R樹稱為區域樹，這是有誤的）。我們就拿二維空間來舉例。下圖是Guttman論文中的一幅圖：

 

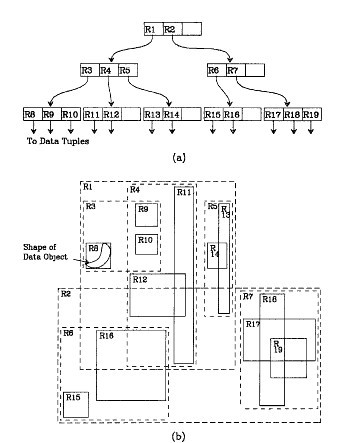
我來詳細解釋一下這張圖。先來看圖（b）

1. 首先我們假設所有資料都是二維空間下的點，圖中僅僅標誌了R8區域中的資料，也就是那個shape of data object。別把那一塊不規則圖形看成一個數據，我們把它看作是多個數據圍成的一個區域。為了實現R樹結構，我們用一個最小邊界矩形恰好框住這個不規則區域，這樣，我們就構造出了一個區域：R8。R8的特點很明顯，就是正正好好框住所有在此區域中的資料。其他實線包圍住的區域，如R9，R10，R12等都是同樣的道理。這樣一來，我們一共得到了12個最最基本的最小矩形。這些矩形都將被儲存在子結點中。
2. 下一步操作就是進行高一層次的處理。我們發現R8，R9，R10三個矩形距離最為靠近，因此就可以用一個更大的矩形R3恰好框住這3個矩形。
3. 同樣道理，R15，R16被R6恰好框住，R11，R12被R4恰好框住，等等。所有最基本的最小邊界矩形被框入更大的矩形中之後，再次迭代，用更大的框去框住這些矩形。

我想大家都應該理解這個資料結構的特徵了。用地圖的例子來解釋，就是所有的資料都是餐廳所對應的地點，先把相鄰的餐廳劃分到同一塊區域，劃分好所有餐廳之後，再把鄰近的區域劃分到更大的區域，劃分完畢後再次進行更高層次的劃分，直到劃分到只剩下兩個最大的區域為止。要查詢的時候就方便了。

下面就可以把這些大大小小的矩形存入我們的R樹中去了。根結點存放的是兩個最大的矩形，這兩個最大的矩形框住了所有的剩餘的矩形，當然也就框住了所有的資料。下一層的結點存放了次大的矩形，這些矩形縮小了範圍。每個葉子結點都是存放的最小的矩形，這些矩形中可能包含有n個數據。

在這裡，讀者先不要去糾結於如何劃分資料到最小區域矩形，也不要糾結怎樣用更大的矩形框住小矩形，這些都是下一節我們要討論的。

講完了基本的資料結構，我們來講個例項，如何查詢特定的資料。又以餐廳為例，假設我要查詢廣州市天河區天河城附近一公里的所有餐廳地址怎麼辦？

1. 開啟地圖（也就是整個R樹），先選擇國內還是國外（也就是根結點）。
2. 然後選擇華南地區（對應第一層結點），選擇廣州市（對應第二層結點），
3. 再選擇天河區（對應第三層結點），
4. 最後選擇天河城所在的那個區域（對應葉子結點，存放有最小矩形），遍歷所有在此區域內的結點，看是否滿足我們的要求即可。

怎麼樣，其實R樹的查詢規則跟查地圖很像吧？對應下圖：

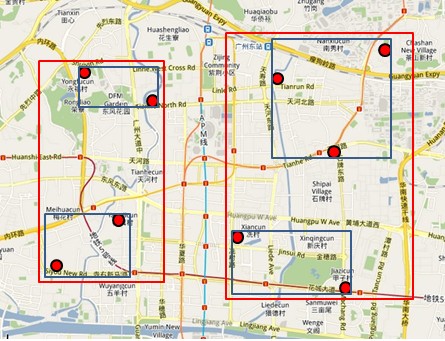
一棵R樹滿足如下的性質：

1.     除非它是根結點之外，所有葉子結點包含有m至M個記錄索引（條目）。作為根結點的葉子結點所具有的記錄個數可以少於m。通常，m=M/2。

2.     對於所有在葉子中儲存的記錄（條目），I是最小的可以在空間中完全覆蓋這些記錄所代表的點的矩形（注意：此處所說的“矩形”是可以擴充套件到高維空間的）。

3.     每一個非葉子結點擁有m至M個孩子結點，除非它是根結點。

4.     對於在非葉子結點上的每一個條目，i是最小的可以在空間上完全覆蓋這些條目所代表的店的矩形（同性質2）。

5.     所有葉子結點都位於同一層，因此R樹為平衡樹。

葉子結點的結構

先來探究一下葉子結點的結構。葉子結點所儲存的資料形式為：(I, tuple-identifier)。

      其中，tuple-identifier表示的是一個存放於資料庫中的tuple，也就是一條記錄，它是n維的。I是一個n維空間的矩形，並可以恰好框住這個葉子結點中所有記錄代表的n維空間中的點。I=(I₀,I₁,…,I_n-1)。其結構如下圖所示：

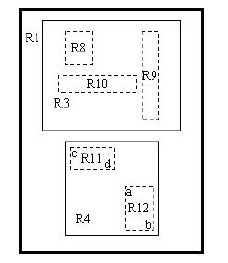
下圖描述的就是在二維空間中的葉子結點所要儲存的資訊。

 

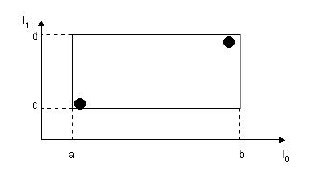
在這張圖中，I所代表的就是圖中的矩形，其範圍是a<=I₀<=b，c<=I₁<=d。有兩個tuple-identifier，在圖中即表示為那兩個點。這種形式完全可以推廣到高維空間。大家簡單想想三維空間中的樣子就可以了。這樣，葉子結點的結構就介紹完了。

非葉子結點

      非葉子結點的結構其實與葉子結點非常類似。想象一下B樹就知道了，B樹的葉子結點存放的是真實存在的資料，而非葉子結點存放的是這些資料的“邊界”，或者說也算是一種索引（有疑問的讀者可以回顧一下上述第一節中講解B樹的部分）。

      同樣道理，R樹的非葉子結點存放的資料結構為：(I, child-pointer)。

      其中，child-pointer是指向孩子結點的指標，I是覆蓋所有孩子結點對應矩形的矩形。這邊有點拗口，但我想不是很難懂？給張圖：

 

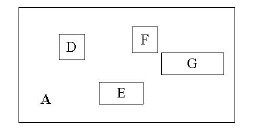
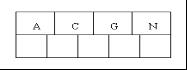
D,E,F,G為孩子結點所對應的矩形。A為能夠覆蓋這些矩形的更大的矩形。這個A就是這個非葉子結點所對應的矩形。這時候你應該悟到了吧？無論是葉子結點還是非葉子結點，它們都對應著一個矩形。樹形結構上層的結點所對應的矩形能夠完全覆蓋它的孩子結點所對應的矩形。根結點也唯一對應一個矩形，而這個矩形是可以覆蓋所有我們擁有的資料資訊在空間中代表的點的。

我個人感覺這張圖畫的不那麼精確，應該是矩形A要恰好覆蓋D,E,F,G，而不應該再留出這麼多沒用的空間了。但為尊重原圖的繪製者，特不作修改。

R樹的操作

這一部分也許是程式設計者最關注的問題了。這麼高效的資料結構該如何去實現呢？這便是這一節需要闡述的問題。

搜尋

R樹的搜尋操作很簡單，跟B樹上的搜尋十分相似。它返回的結果是所有符合查詢資訊的記錄條目。而輸入是什麼？就我個人的理解，輸入不僅僅是一個範圍了，它更可以看成是一個空間中的矩形。也就是說，我們輸入的是一個搜尋矩形。

先給出虛擬碼：

Function：Search

描述：假設T為一棵R樹的根結點，查詢所有搜尋矩形S覆蓋的記錄條目。

S1:[查詢子樹] 如果T是非葉子結點，如果T所對應的矩形與S有重合，那麼檢查所有T中儲存的條目，對於所有這些條目，使用Search操作作用在每一個條目所指向的子樹的根結點上（即T結點的孩子結點）。

S2:[查詢葉子結點] 如果T是葉子結點，如果T所對應的矩形與S有重合，那麼直接檢查S所指向的所有記錄條目。返回符合條件的記錄。

我們通過下圖來理解這個Search操作。

 

 

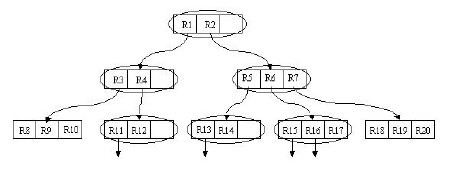
陰影部分所對應的矩形為搜尋矩形。它與根結點對應的最大的矩形（未畫出）有重疊。這樣將Search操作作用在其兩個子樹上。兩個子樹對應的矩形分別為R1與R2。搜尋R1，發現與R1中的R4矩形有重疊，繼續搜尋R4。最終在R4所包含的R11與R12兩個矩形中查詢是否有符合條件的記錄。搜尋R2的過程同樣如此。很顯然，該演算法進行的是一個迭代操作。

插入

      R樹的插入操作也同B樹的插入操作類似。當新的資料記錄需要被新增入葉子結點時，若葉子結點溢位，那麼我們需要對葉子結點進行分裂操作。顯然，葉子結點的插入操作會比搜尋操作要複雜。插入操作需要一些輔助方法才能夠完成。

來看一下虛擬碼：

Function：Insert

描述：將新的記錄條目E插入給定的R樹中。

I1：[為新記錄找到合適插入的葉子結點] 開始ChooseLeaf方法選擇葉子結點L以放置記錄E。

I2：[新增新記錄至葉子結點] 如果L有足夠的空間來放置新的記錄條目，則向L中新增E。如果沒有足夠的空間，則進行SplitNode方法以獲得兩個結點L與LL，這兩個結點包含了所有原來葉子結點L中的條目與新條目E。

I3：[將變換向上傳遞] 開始對結點L進行AdjustTree操作，如果進行了分裂操作，那麼同時需要對LL進行AdjustTree操作。

I4：[對樹進行增高操作] 如果結點分裂，且該分裂向上傳播導致了根結點的分裂，那麼需要建立一個新的根結點，並且讓它的兩個孩子結點分別為原來那個根結點分裂後的兩個結點。

Function：ChooseLeaf

描述：選擇葉子結點以放置新條目E。

CL1：[Initialize] 設定N為根結點。

CL2：[葉子結點的檢查] 如果N為葉子結點，則直接返回N。

CL3：[選擇子樹] 如果N不是葉子結點，則遍歷N中的結點，找出新增E.I時擴張最小的結點，並把該結點定義為F。如果有多個這樣的結點，那麼選擇面積最小的結點。

CL4：[下降至葉子結點] 將N設為F，從CL2開始重複操作。

Function：AdjustTree

描述：葉子結點的改變向上傳遞至根結點以改變各個矩陣。在傳遞變換的過程中可能會產生結點的分裂。

AT1：[初始化] 將N設為L。

AT2：[檢驗是否完成] 如果N為根結點，則停止操作。

AT3：[調整父結點條目的最小邊界矩形] 設P為N的父節點，E_N為指向在父節點P中指向N的條目。調整EN.I以保證所有在N中的矩形都被恰好包圍。

AT4：[向上傳遞結點分裂] 如果N有一個剛剛被分裂產生的結點NN，則建立一個指向NN的條目E_NN。如果P有空間來存放E_NN，則將E_NN新增到P中。如果沒有，則對P進行SplitNode操作以得到P和PP。

AT5：[升高至下一級] 如果N等於L且發生了分裂，則把NN置為PP。從AT2開始重複操作。

同樣，我們用圖來更加直觀的理解這個插入操作。

 

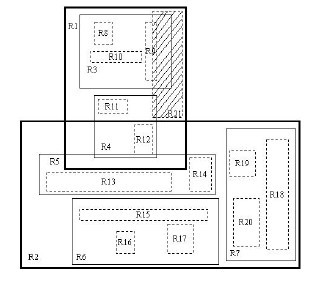
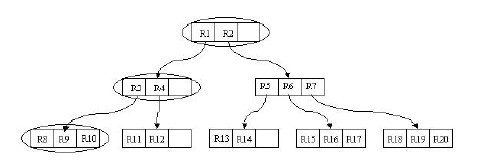
    我們來通過圖分析一下插入操作。現在我們需要插入R21這個矩形。開始時我們進行ChooseLeaf操作。在根結點中有兩個條目，分別為R1，R2。其實R1已經完全覆蓋了R21，而若向R2中新增R21，則會使R2.I增大很多。顯然我們選擇R1插入。然後進行下一級的操作。相比於R4，向R3中新增R21會更合適，因為R3覆蓋R21所需增大的面積相對較小。這樣就在B8，B9，B10所在的葉子結點中插入R21。由於葉子結點沒有足夠空間，則要進行分裂操作。

    插入操作如下圖所示：

這個插入操作其實類似於第一節中B樹的插入操作，這裡不再具體介紹，不過想必看過上面的虛擬碼大家應該也清楚了。

刪除

R樹的刪除操作與B樹的刪除操作會有所不同，不過同B樹一樣，會涉及到壓縮等操作。相信讀者看完以下的虛擬碼之後會有所體會。R樹的刪除同樣是比較複雜的，需要用到一些輔助函式來完成整個操作。

虛擬碼如下：

Function：Delete

描述：將一條記錄E從指定的R樹中刪除。

D1：[找到含有記錄的葉子結點] 使用FindLeaf方法找到包含有記錄E的葉子結點L。如果搜尋失敗，則直接終止。

D2：[刪除記錄] 將E從L中刪除。

D3：[傳遞記錄] 對L使用CondenseTree操作

D4：[縮減樹] 當經過以上調整後，如果根結點只包含有一個孩子結點，則將這個唯一的孩子結點設為根結點。

Function：FindLeaf

描述：根結點為T，期望找到包含有記錄E的葉子結點。

FL1：[搜尋子樹] 如果T不是葉子結點，則檢查每一條T中的條目F，找出與E所對應的矩形相重合的F（不必完全覆蓋）。對於所有滿足條件的F，對其指向的孩子結點進行FindLeaf操作，直到尋找到E或者所有條目均以被檢查過。

FL2：[搜尋葉子結點以找到記錄] 如果T是葉子結點，那麼檢查每一個條目是否有E存在，如果有則返回T。

Function：CondenseTree

描述：L為包含有被刪除條目的葉子結點。如果L的條目數過少（小於要求的最小值m），則必須將該葉子結點L從樹中刪除。經過這一刪除操作，L中的剩餘條目必須重新插入樹中。此操作將一直重複直至到達根結點。同樣，調整在此修改樹的過程所經過的路徑上的所有結點對應的矩形大小。

CT1：[初始化] 令N為L。初始化一個用於儲存被刪除結點包含的條目的連結串列Q。

CT2：[找到父條目] 如果N為根結點，那麼直接跳轉至CT6。否則令P為N 的父結點，令E_N為P結點中儲存的指向N的條目。

CT3：[刪除下溢結點] 如果N含有條目數少於m，則從P中刪除E_N，並把結點N中的條目新增入連結串列Q中。

CT4：[調整覆蓋矩形] 如果N沒有被刪除，則調整E_N.I使得其對應矩形能夠恰好覆蓋N中的所有條目所對應的矩形。

CT5：[向上一層結點進行操作] 令N等於P，從CT2開始重複操作。

CT6：[重新插入孤立的條目] 所有在Q中的結點中的條目需要被重新插入。原來屬於葉子結點的條目可以使用Insert操作進行重新插入，而那些屬於非葉子結點的條目必須插入刪除之前所在層的結點，以確保它們所指向的子樹還處於相同的層。

      R樹刪除記錄過程中的CondenseTree操作是不同於B樹的。我們知道，B樹刪除過程中，如果出現結點的記錄數少於半滿（即下溢）的情況，則直接把這些記錄與其他葉子的記錄“融合”，也就是說兩個相鄰結點合併。然而R樹卻是直接重新插入。

同樣，我們用圖直觀的說明這個操作。

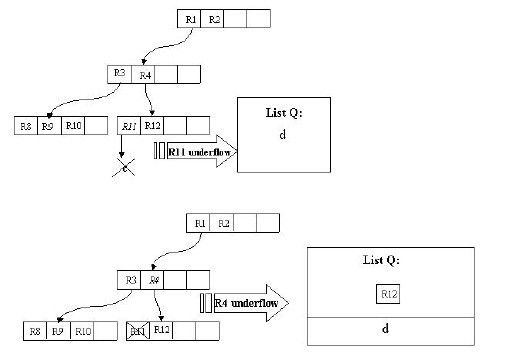
假設結點最大條目數為4，最小條目數為2。在這張圖中，我們的目標是刪除記錄c。首先使用FindLeaf操作找到c所處在的葉子結點的位置——R11。當c從R11刪除時，R11就只有一條記錄了，少於最小條目數2，出現下溢，此時要呼叫CondenseTree操作。這樣，c被刪除，R11剩餘的條目——指向記錄d的指標——被插入連結串列Q。然後向更高一層的結點進行此操作。這樣R12會被插入連結串列中。原理是一樣的，在這裡就不再贅述。

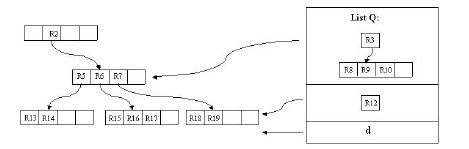
有一點需要解釋的是，我們發現這個刪除操作向上傳遞之後，根結點的條目R1也被插入了Q中，這樣根結點只剩下了R2。彆著急，重新插入操作會有效的解決這個問題。我們插入R3，R12，d至它原來所處的層。這樣，我們發現根結點只有一個條目了，此時根據Inert中的操作，我們把這個根結點刪除，它的孩子結點，即R5，R6，R7，R3所在的結點被置為根結點。至此，刪除操作結束。

結語

      R樹是一種能夠有效進行高維空間搜尋的資料結構，它已經被廣泛應用在各種資料庫及其相關的應用中。但R樹的處理也具有侷限性，它的最佳應用範圍是處理2至6維的資料，更高維的儲存會變得非常複雜，這樣就不適用了。近年來，R樹也出現