資料庫索引的基石----B樹
資料結構相對來說比較枯燥, 我儘量用最易懂的話,來把B樹講清楚。
學過資料結構的人都接觸過一個概念二叉樹,簡單來說,就是每個父節點最多有兩個子節點。
為了在二叉樹上更快的進行元素的查詢,人們通過不斷的改進,從而設計出平衡二叉查詢樹,也就是這個樣子:

平衡二叉查詢樹的特性由於不是本文的重點,這裡就不再展開了。值得一提的是平衡二叉查詢樹已經基本滿足了我們平常的軟體開發需求了。但是對於一些需要持久化資料並且支援查詢的業務來說,平衡二叉查詢樹存在一個明顯的問題:
如果資料已經持久化到硬盤裡邊,而我們又想要查詢資料的話,我們需要把資料先載入到記憶體裡邊再進行比較。
但是,想一想你是不是沒法直接判斷硬盤裡邊包含某一段關鍵字?
如果想要判斷,必須要先把資料讀到記憶體裡邊才可以。如果資料量小的話,這種載入硬碟資料的效能損耗基本可以忽略掉,可是如果資料量大的話,你總不能一次把全部資料載入到記憶體中再計算。即使你能等,記憶體也支撐不住。所以我們的辦法就是分段查詢,一段一段的取到記憶體裡邊進行比較,可是這樣無論是取多大,怎麼比較,又是一個問題。而且更要命的是,倘若過於頻繁的一段段從硬碟中取資料的話,浪費在讀取資料的效能實在讓人可惜。
基於種種原因,於是有人對平衡二叉查詢樹提出了改良:
1970年Rudolf Bayer,Edward M. McCreight 首次在論文中提到了一種新型的樹,並且稱之為B樹,意味balance tree 平衡樹,也稱之為 B-樹(千萬不可稱之為B減樹哦),B_樹等。

接著為了增加子節點繼續擴充套件的能力,允許一個節點可以多叉,但是依賴的原則還是基本不變的:每一個節點(更準確的說法是關鍵字)的左分叉要比當前節點的數字小,右分叉要比當前節點數字大。
所以我們基本可以理解為
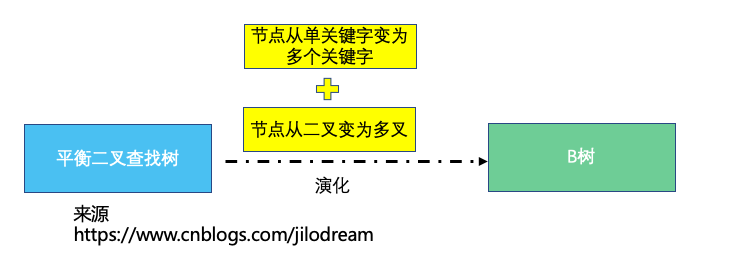
B樹=節點從單一關鍵字擴充套件成多關鍵字+二叉擴充套件為多叉。到這裡,我們基本就算是搞懂B樹是什麼樣子了。
試想一下,如果是這個樣子的話,我們的程式就可以先把資料按照節點為單位,一次讀取若干個關鍵字到記憶體中。(防盜連線:本文首發自http://www.cnblogs.com/jilodream/ )然後在記憶體中進行比較,接著確定好目標所在的下一個分叉,然後獲取下一個分叉節點的資料。大概是下邊這個樣子:
但是出於更嚴格要求,B樹的定義要複雜的多。
首先我們要明白一個詞:階 degree
這個詞用來描述一個節點能包含的最大關鍵字的孩子的個數,也就是說節點最多有多少個分叉,而節點能裝的關鍵字的個數,就是分叉樹-1.
注意這個階是不隨著節點關鍵字的增加和減少來改變的,而是最初定義的一個屬性。節點增加關鍵字和減少關鍵字都不會改變這個樹最初定義的階的。
接下來圍繞這個階我們設定一些規則,保證B樹增加和減少關鍵字後,整個樹仍然是高效可用的。
(1) 樹中每個節點最多有m個孩子
直白的說:每個節點最多有m個分叉
(2) 除去根節點這葉子節點外,其它節點至少有m/2個孩子
(3) 根節點至少有2個孩子
直白的說:如果是樹中間的節點(非根非葉子),那麼每個節點至少都有一半的分叉有孩子,如果是根節點那麼就最少有2個孩子
(4) 所有葉節點在同一層,B樹的葉節點可以看成是一種外部節點,不包含任何資訊
直白的說:所有的葉節點都和高度最高的葉節點呢,畫在一個水平線上,這些葉子節點呢,是用來記錄外部資訊的。可以用空指標表示,代表查詢失敗到達的位置。
(5) 有k個關鍵字(注意節點中的關鍵字要排好順序)的非葉節點恰好有k+1個孩子。
直白的說:1、節點中的關鍵字排好順序,這樣方便我們查詢
2、有k個關鍵字就要有k+1個分叉(孩子)
如下圖,就是一個多層的B樹了,但是要注意,這棵B樹畫的並不標準,最下層的節點並非葉子,葉子節點是基於這一層節點作為父節點的子節點,在圖中葉子節點沒有被畫出來。(參考第四條)

接下來基於這棵B樹,我們舉個例子,來查詢17這個數字:
第一步:記憶體載入根節點13,我們比較發現17>13,找13的右側分叉節點(15,20)
第二步:記憶體載入節點(15,20),我們比較15,發現 17>15,再比較20,發現17<20,於是取出15的右側分叉節點(16,17)
第三步:記憶體載入節點(16,17),我們比較16,發現17>16,再比較17,發現17=17,發現命中,取出17所對應的資料。
我們再舉個例子,來查詢18這個數字:
前兩步都相同
第三步:記憶體載入節點(16,17),我們比較16,發現18>16,再比較17,發現18>17,於是我們要找17右側的分叉,但是此時右側的葉子節點為空(17的右側分叉對應葉子節點,葉子節點為空),所以我們斷定,18不存在。
注意無論是否存在,我們最多都只用了3次記憶體載入,就完成了比較查詢。
這裡要特別提下,為啥我們只看重記憶體載入的速度,而忽略比較次數的耗時呢?(防盜連線:本文首發自http://www.cnblogs.com/jilodream/ )這是因為我們在分析效能問題時,需要著重效能的瓶頸來分析。磁碟的讀取和記憶體的訪問接近有5個數量級的差異(單位大概是10毫秒與50微秒的差距)。因此我們在這裡比較效能時,就是要看進行了多少次磁碟的讀取(磁碟的IO),並且主要以減少磁碟IO的手段來提升效能。
當然為了提升比較次數,我們還可以採用二分查詢的方式,來判斷節點中是否包含某個關鍵字,進一步加快速度。
接下來影響提升整個IO次數的瓶頸就出現在,一個節點到底能儲存多少個關鍵字,如果關鍵字儲存的越多,我們一次載入到記憶體中的資料也就越多。同時也要注意,這個關鍵字的個數不能設定成無限大,因為記憶體不足以支撐一次載入太多的資料。
基於以上種種,我們可以發現,B樹是基於傳統硬碟與記憶體之間的IO差距,而專門設計出來的資料結構,他天然就適用於檔案系統。
而對於B樹的升級版B+樹(B plus tree),我會在接下來的文章中專門講講,它又有什麼不一樣的地方。<
