時間複雜度是一個函式，它定量描述了該演算法的執行時間。常見的時間複雜度有以下幾種。
1，log(2)n，n，n log(2)n ，n的平方，n的三次方，2的n次方，n!

1指的是常數。即，無論演算法的輸入n是多大，都不會影響到演算法的執行時間。這種是最優的演算法。而n！（階乘）是非常差的演算法。當n變大時，演算法所需的時間是不可接受的。

用通俗的話來描述，我們假設n=1所需的時間為1秒。那麼當n = 10，000時。
O（1）的演算法需要1秒執行完畢。
O（n）的演算法需要10，000秒 ≈ 2.7小時 執行完畢。

O（n2）的演算法需要100，000，000秒 ≈ 3.17年 執行完畢。
O（n！）的演算法需要XXXXXXXX(系統的計算器已經算不出來了)。
可見演算法的時間複雜度影響有多大。

所以O（1）和O（n）差了2.7小時，區別顯而易見。

-----------------------------------------  實戰分割線 ------------------------------------------------

假如一張表有一億條資料 ，需要查詢其中某一條資料，按照常規邏輯， 一條一條的去匹配的話， 最壞的情況下需要匹配一億次才能得到結果，用大O標記法就是O(n)最壞時間複雜度，這是無法接受的，而且這一億條資料顯然不能一次性讀入記憶體供程式使用， 因此， 這一億次匹配在不經快取優化的情況下就是一億次IO開銷，以現在磁碟的IO能力和CPU的運算能力， 有可能需要幾個月才能得出結果 。如果把這張錶轉換成平衡樹結構（一棵非常茂盛和節點非常多的樹），

(圖示:該樹只有三個節點)

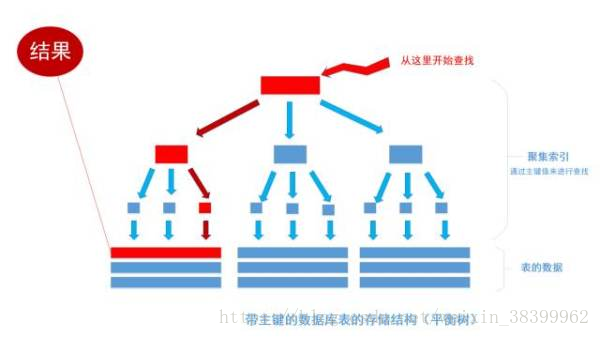
假設這棵樹有10層，那麼只需要10次IO開銷就能查詢到所需要的資料， 速度以指數級別提升，用大O標記法就是O(log n)，n是記錄總樹，底數是樹的分叉數，結果就是樹的層次數。換言之，查詢次數是以樹的分叉數為底，記錄總數的對數，用公式來表示就是

用程式來表示就是Math.Log(100000000,10)，100000000是記錄數，10是樹的分叉數（真實環境下分叉數遠不止10）， 結果就是查詢次數，這裡的結果從億降到了個位數。因此，利用索引會使資料庫查詢有驚人的效能提升。