淺析三種多路搜尋樹
B樹家族
磁碟I/O操作的基本單位為塊。從磁碟上讀取資訊時,會把包含資訊的整個塊讀入記憶體;將資訊儲存到磁碟上時,也需要將整個塊寫到磁碟上。當每次從磁碟上請求資訊時,都必須先在磁碟上定位該資訊。磁頭移動到包含所請求資訊的磁碟位置上方。然後,將磁碟旋轉,將磁頭下方的整個塊傳送到記憶體。也就是說,資料訪問時間由幾個時間段組成:
- 訪問時間=尋道時間+轉動延遲+資料傳送時間
與在記憶體中傳送資訊相比,這個過程是相當緩慢的,其中尋道時間由於倚賴與磁頭在定位到正確的磁軌過程中的磁頭的機械運動是非常消耗時間的。轉動延遲指的是磁頭轉動到正確的磁碟塊所需的時間。
如果程式需要不斷的使用輔助儲存器上的資訊,在設計該程式時就應該考慮這種儲存方式的特性。如果用平衡樹(AVL,RB)來作為這種儲存方式的資料結構,那麼平衡樹可能分佈在磁碟的不同塊上,所以平均需要訪問兩個磁碟塊。如果程式經常使用該樹,這種訪問時間就會顯著增加。此外在該樹中的插入和刪除鍵值也需要訪問多個個磁碟塊。可以看出,平衡樹在記憶體中是一種非常高效的工具,而在磁碟上就會變得非常的低效。在涉及輔助儲存器時,二叉查詢樹在其他方面的效能優點會變得微不足道,因為這種方法需要不斷的訪問輔助儲存器,嚴重降低了效能。
在磁碟上一次存取大量資料比在磁碟上的不同部分存取少量資料更好,比如給磁碟傳送10KB資料時:
- 一個10KB片段上:
訪問時間=40ms(尋道)+10ms(轉動延遲)+10ms(資料傳送)=60ms
兩個5KB片段上:
訪問時間=2*(40 + 10 +5)=110ms
訪問時間幾乎是在一個片段上的兩倍,因為每次磁碟訪問都是很浪費時間的。如果可能,資料應該儘量使訪問磁碟的次數減少。
B樹
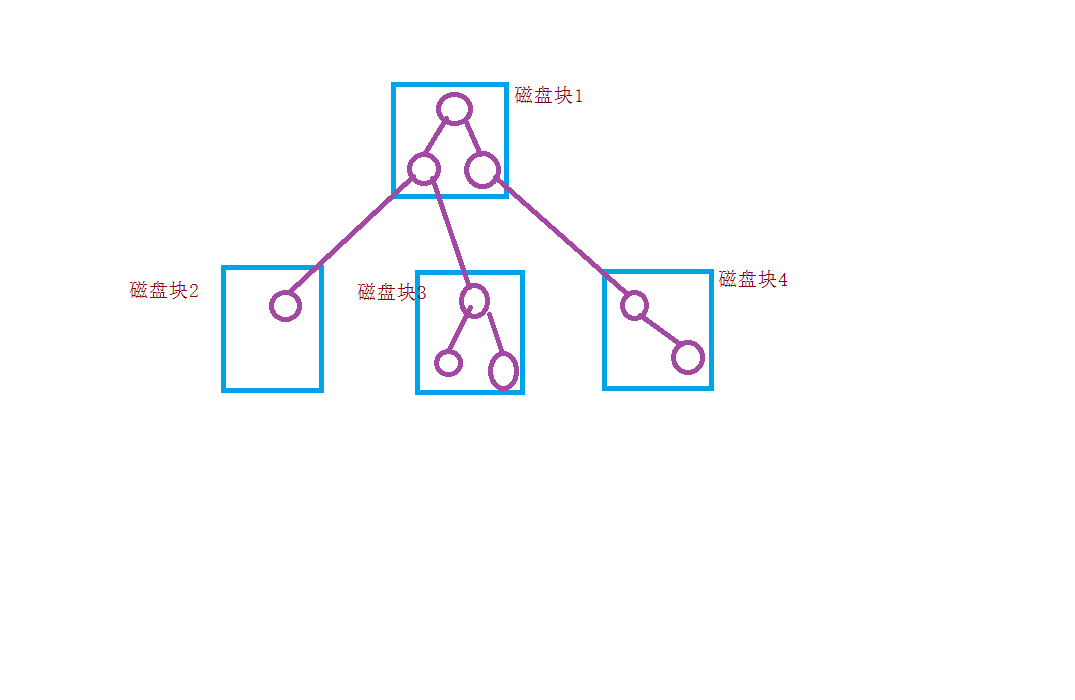
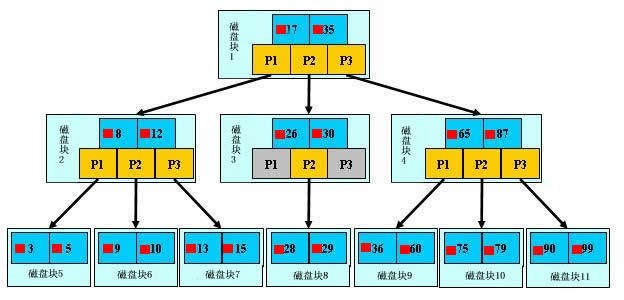
B樹主要操作輔助儲存器,並儘可能減小由這類儲存器帶來的影響。它的一個重要的特點是每個節點的大小可以與磁碟塊的大小相等。節點中鍵值的數量可以根據可以根據鍵值的大小,資料的組織方式和磁碟塊的大小而定。
一個M階B樹是具有以下性質的多叉查詢樹:
- 1 . 根節點至少有兩個孩子
- 2 . 每個非根節點有[M/2 , M]個孩子
- 3 . 每個非根節點有[ M-1/2 , M-1 ]個關鍵字,並且以升序排列
- 4 . key [i]和key [i+ 1 ]之間的孩子節點的值介於key [i]、key [i+ 1 ]之間
- 5 . 所有的葉子節點都在同一層
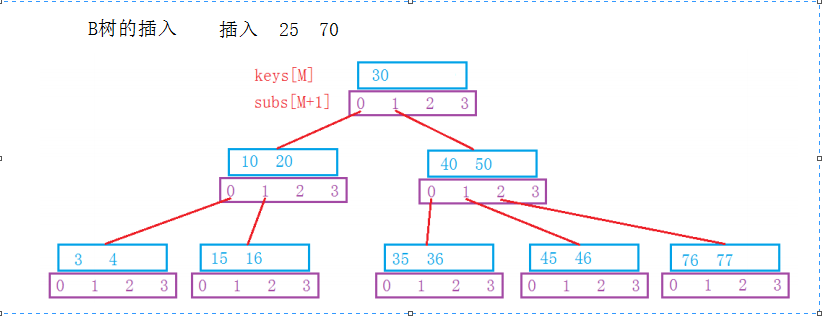
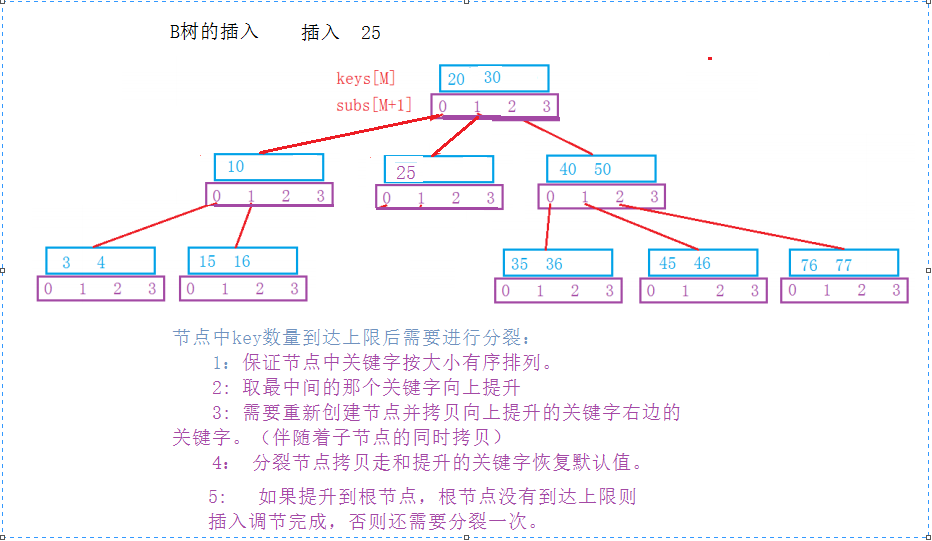
B樹鍵值的插入
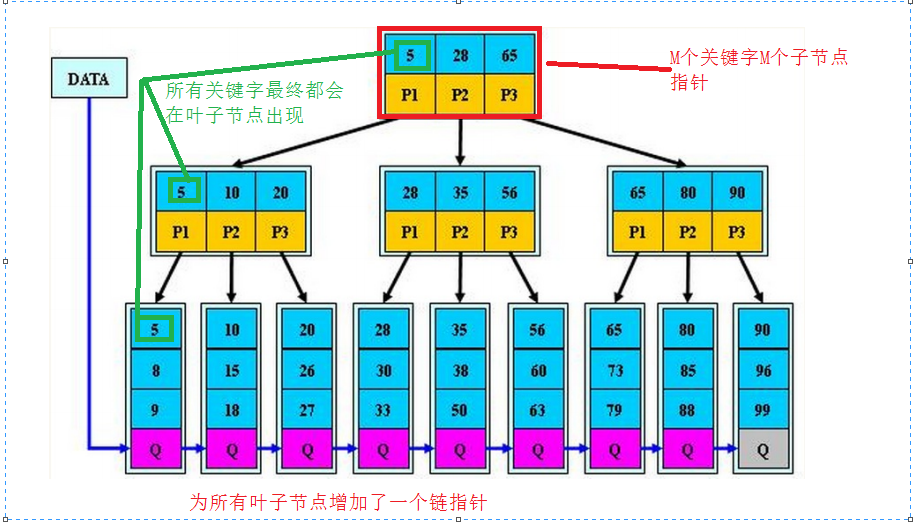
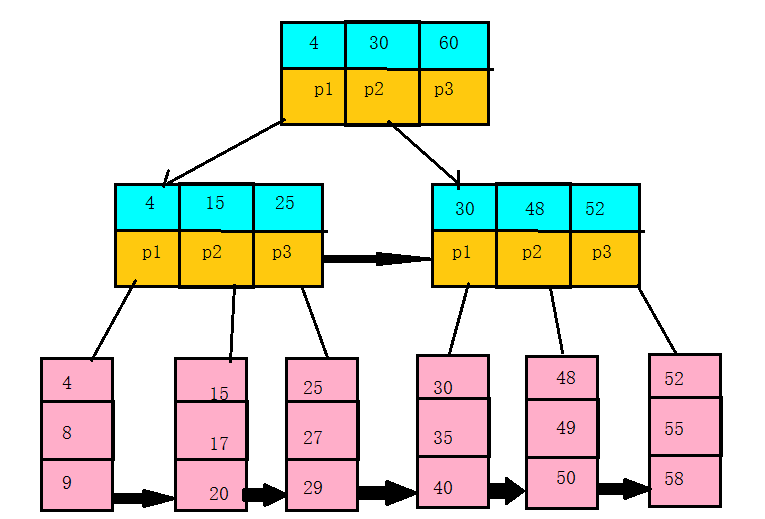
B+樹
B+樹其實是B樹的變體,它的基本定義與B樹相同,除了以下部分:
- 非葉子節點指標和節點中關鍵字的個數相等。
- 非葉子節點的指標p[i]指向關鍵字在_keys[i]和_keys[i+1]之間的子樹(前開後閉區間)。
為所非葉子節點增加一個鏈指標,方便遍歷。
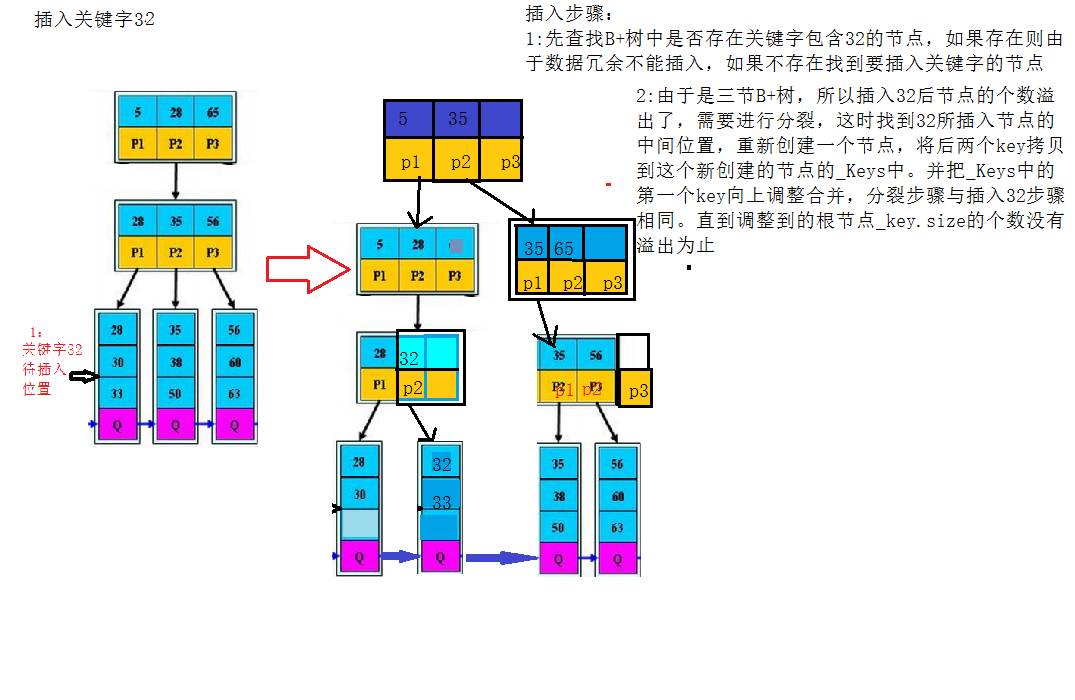
B+樹鍵值的插入
B*樹
B*樹也是B樹的一個變種。在B*樹中除了根節點外,其他節點都必須至少2/3滿,而不能像樹一樣半滿,並且B*樹相比於B樹在非葉子節點和葉子節點上都增加了指向兄弟節點的指標。
B*樹的插入
在B*樹中,為了延遲分解,當節點溢位時,會嘗試在節點及其同級節點之間重新分配鍵值,如果其同級節點也是滿的,就要分解節點建立一個新節點,將原節點及其同級節點以及父節點的鍵值重新分配到三個節點,用於劃分三個節點的兩個鍵值放入父節點,從而保證了2/3的填充率。