資料結構

一、概述

1、資料結構三要素

答：分別是：邏輯結構、儲存結構、資料的運算

2、資料結構構成

答：資料構成見下圖：

資料項：最小的資料單位； 資料元素：是組成資料的、有一定意義的基本單位，主要由資料項構成； 資料物件：是性質相同的資料元素的集合，是資料的子集，主要由資料元素構成； 抽象資料型別：一個數學模型以及定義在此模型上的一組操作。其三個組成部分為：資料物件、資料關係和基本操作。可以用抽象資料型別完整定義資料結構。

3、常見線性與非線性資料結構 && 順序儲存結構與鏈式儲存結構

答：（1）線性結構指的是邏輯結構，而不是物理儲存結構。

常用的線性結構有:線性表，棧（順序棧和鏈式棧），佇列，雙佇列，迴圈佇列、一維陣列，串。（其中棧和佇列只是一種邏輯存在的，實際中不存在）

常見的非線性結構有:二維陣列，多維陣列，廣義表，樹(二叉樹等)，圖。

（2）常見的順序儲存結構很多，如陣列就是順序儲存，注意幾種資料結構中：棧和佇列都可以使用順序儲存結構，也可以鏈式儲存結構；堆由於本來就是由一維陣列進化而來，故也可以順序儲存；最重要注意，二叉樹只有完全二叉樹或滿二叉樹才可以順序儲存。

二、線性表

1、線性表

（1）定義：就是一個表，一個記錄就是線性表的一個數據元素，表的長度就是資料元素的個數。

如圖，線性連結串列由一個個結點組成，每個節點有資料域和指標域兩部分組成：資料域（本結點儲存的資料資訊）與指標域（下一個結點的儲存位置）；

（2）線性連結串列不要求書寫格式上連續，存線上性儲存和鏈式儲存，兩種儲存方式各有優劣，需根據資料操作型別選擇合適的儲存方式，沒有優先級別。

（3）補充：迴圈連結串列：最後一個結點指向頭結點，形成一個環；雙向連結串列：比線性連結串列多一個指標域，用於指向直接前趨。

三、棧和佇列、串、陣列和廣義表

1、棧

答：（1）分為順序棧和鏈棧（不需要頭結點）；若陣列實現，需要事先確定棧的容量；若用指標實現，可以無限增長。

（2）棧是在記憶體中開闢的一段連續的儲存區，將棧中資料從棧底到棧頂依次存放。同時設定base和top指標，base指向棧底元素位置，top指向棧頂元素後一個位置。
①棧的插入與刪除（入棧與出棧）都在棧頂操作；
棧為空時，base=top，若為順序棧例如S(1:m)，用下標代表地址的話，空棧base=top=1，向棧中插入一個元素，top就向棧頂方向自增1，這也是為什麼非空時，top指向棧頂元素後一個位置。
棧為滿時，top指標指向最後一個棧元素的後一位置，就是指向棧外。若為順序棧S(1:m)，那麼棧滿可以表示為top=m+1。
注：棧的資料溢位時，可以根據棧自增量進行拓展棧的容量。
②棧就是一種特殊的線性表。

2、佇列

答：（1）順序佇列：需設定隊首指標和隊尾指標，需事先設定隊的容量；鏈佇列（指標實現，不需設定容量，可以設定頭結點）
（2）佇列是將資料從隊頭至隊尾依次存放在一段連續的儲存區中，該儲存區不可拓展。分別設定front和rear指向隊頭元素位置和隊尾元素的後一個位置。注意：front=rear時，隊為空。
（3）佇列的插入與刪除
佇列用陣列表示，一般front在陣列低下標處，rear在陣列高下標處。所以插入刪除如下：
①插入（入隊）在隊尾操作，rear自增1；刪除（出隊）在隊頭處操作，front自增1（注意，刪除與棧操作不同）。
②佇列的插入刪除時間複雜度都為o(1)，刪除直接用尾指標即可；

（4）佇列和線性表類似，也有順序儲存和鏈式儲存兩種方式。佇列就是一種特殊的線性表。

3、迴圈佇列

答：（1）因為佇列的刪除會造成rear-front小於佇列容量，故常常使用迴圈佇列解決此問題。
迴圈佇列就是當rear出界但佇列因為刪除使得front前空出一段儲存空間時，可將rear對應資料移到front前面的區域，並依次儲存，同時rear也要移到對應資料後一個位置。如果front=(rear+1 )%QueueSIze，則表示迴圈佇列已滿（迴圈佇列滿時，最後一個數據和首資料之間還空一個，rear此時指向這裡）。
（2）判斷迴圈佇列中元素個數（m為佇列設定容量）：
如果 rear>front，n=rear-front；
如果 rear<front，n=m-(front-rear)；

4、串

答：定義：就是字串，有子串和主串之分。分為定長順序儲存（儲存容量有限）和堆分配儲存（儲存容量動態分配）。

5、陣列和廣義表

答：（1）陣列略；

（2）廣義表定義：是一種非線性的資料結構，是線性表的一種推廣。即廣義表中放鬆對錶元素的原子限制，容許它們具有其自身結構。廣義表的資料元素除了可以是線性表中定義的原子外，還可以是表，具體的元素如下：

表結點hp:子表頭指標域， tp:子表尾指標域

注：廣義表採用鏈式儲存結構

6、廣義表及其運算

答：廣義表是線性表的推廣，只不過其原子型別不受限制，容許它們具有其自身結構,可以是子表等。例如：廣義表LS=((a,b,c),(d,e,f))。
廣義表可以用樹結構表示； 廣義表中的兩個基本運算：head和tail：
head(LS)：取表頭，返回值可以是單元素也可以是子表，即廣義表第一個元素。
tail(LS)：取表尾，將原廣義表去掉表頭後新生成的廣義表就是返回值，注：tail返回值一定是廣義表，而且是和原表同級別的表。比如上述LS的tail運算結果就是((d,e,f))，就是原表去掉首元素後的結果。

5、稀疏矩陣與三元組

答：（1）稀疏矩陣：對於那些零元素數目遠遠多於非零元素數目，並且非零元素的分佈沒有規律的矩陣稱為稀疏矩陣（sparse）；

①稀疏矩陣的壓縮：由於稀疏矩陣中非零元素較少，零元素較多，因此可以採用只儲存非零元素的方法來進行壓縮儲存。因為非

零元素分佈沒有任何規律，所以在進行壓縮儲存的時侯需要儲存非零元素值的同時還要儲存非零元素在矩陣中的位置，即非零元素

所在的行號和列號。

②壓縮方式：三元組、十字連結串列法（其中十字連結串列更適合矩陣的加法乘法等操作）；

（2）三元組：

三元組可以採用順序表示方法，也可以採用鏈式表示方法，這樣就產生了對稀疏矩陣的不同壓縮儲存方式。順序儲存可如下：

順序表中除了儲存三元組外，還應該儲存矩陣行數、列數和總的非零元素數目，這樣才能唯一的確定一個矩陣，如圖：

三元組做到下面三條便可實現矩陣的轉置：

①將矩陣的行列值交換。

②將每個三元組中的 i 和 j 相互調換。

③重排三元組之間的次序，即行列互換後，還要恢復原儲存的順序。

四、樹與二叉樹

1、樹和二叉樹

答：（1）樹的作用：用於表示元素和元素之間有分支和層次關係的資料結構；
（2）樹的幾個概念：度——結點的子樹分支樹個數；葉子——最下面的結點；深度——一個樹的最大層次。
（3） 二叉樹：二叉樹的儲存結構分為順序儲存和鏈式儲存；
一個二叉樹，葉子結點為N0，度為2的結點數為N2，那麼N0=N2+1；
一個擁有N個結點的完全二叉樹的深度為[log2N]+1；
順序儲存：只適合完全二叉樹，按照二叉樹的結點序號依次從左到右（或從上到下）儲存。
鏈式儲存：有兩種形式（2指標域和3指標域），如下圖。

2、線索二叉樹

答：線索二叉樹：以連結串列形式儲存，結點結構如下：

3、二叉樹線索化

答：（1）對二叉樹線索化，實際上就是遍歷二叉樹，檢查當前結點的左、右指標是否為空，如果為空，將它們改為指向前驅結點或後繼結點的線索。

前驅與後繼根據不同遍歷有不同的值，如前序遍歷ABC中B是A的後繼，中序遍歷結果為BAC，B就變成了A的前驅。

（2）過程：

實現二叉樹線索化，樹結點的結構需要增加左右兩個tag，用於標識左右指標域是指向左右子樹還是指向前繼後驅。如圖：

1）先將二叉樹中左右指標域有空的結點標記出來，左指標空就Lf=1，右則Rf=1；

2）然後進行遍歷（根據要求進行前序、中序或後序遍歷），將遍歷結果放在佇列中；

3）根據1）的結果給有空指標的結點新增線索，Lf=1則將相應結點的左指標指向其所在佇列位置的前一個元素（前驅），Rf=1則將相應結點的右指標指

向其所在佇列位置的後一個元素（後繼）。佇列第一個元素左指標忽略，佇列最後一個元素右指標忽略。

（3）二叉樹線索化的意義：

若給二叉樹每個節點增加一個左指標和右指標，那麼共有2n個指標域。由於二叉樹只有n-1個邊，那麼就會有n+1個指標域空著。所以，為了充分利用這些指標域，並把二叉樹遍歷資訊儲存下來，就可以使用二叉樹線索化來實現。線索化後，只要根據線索表中的節點前驅後繼關係進行連線就可以得到二叉樹遍歷序列。

4、赫夫曼樹及應用

答：定義：赫夫曼樹又名最優二叉樹，是帶全路徑長度最小的二叉樹。如下圖：

注意：赫夫曼樹並不是滿二叉樹，是正則二叉樹（也叫正規二叉樹或最優二叉樹），在構造哈夫曼樹時,是從葉子節點向根節點的方向進行的,每次都是兩個兩個成對來形成一個新的分支節點，所以不存在度為1的節點，即其中只有度為0和度為2的結點，因為：
n0 = n2 + 1；//這是二叉樹中固有的公式（n0是度為0的結點數，n2是度為2的結點數），具體可見公式推理
n = n0 + n2；//n為所有結點數
所以 n = 2n0 - 1，即n0 = (n + 1) / 2；
又葉子結點n0對應的即是不同的編碼，所以在赫夫曼編碼中有多少個葉子節點就能得到多少個碼字。

5、赫夫曼樹編碼

答：赫夫曼樹並不是滿二叉樹，是正則二叉樹（也叫正規二叉樹或最優二叉樹），在構造哈夫曼樹時,是從葉子節點向根節點的方向進行的,每次都是兩個兩個成對來形成一個新的分支節點，所以不存在度為1的節點，即其中只有度為0和度為2的結點(附帶一個二叉樹結論：n0=n2+1，其中，n0是度為0的結點數，n2是度為2的結點數)。結點關係有如下：
n=n0+n2;
n=2*n2+1;同時。赫夫曼樹的帶權值最優路徑是所有葉子節點的帶權路徑之和。
此外，赫夫曼樹還有一條規定：左右孩子權值之和為父結點權值，WPL=∑w*l（w為個葉子權值，l為葉子的(深度-1)）。注意：上述是常見的赫夫曼樹，除此之外還有度不為2的，也叫最優m叉樹。其結點也只有度為0和度為m兩種，即X+n0=n（X為度m的結點數，n為總結點數）。那麼其結點關係也有如下：
n=X+n0;
n=m*X=1；赫夫曼樹的生成：前提是給定所有葉子結點的權值序列。
1）從序列中找出權值最小的兩個節點，作為最底層葉子節點並求和得到父節點，生成子樹；
2）然後從剩下的序列和上述子樹根節點中找出最小的兩個並求和，生成新的子樹；
3）重複1）、2）步驟。
如圖：
赫夫曼編碼（字首編碼）：
1）將給定字串根據每個符號出現次數的大小，重新排序成一個字元頻率由小到大的表格，如圖：

2）將字元頻率作為權值，對字元進行赫夫曼樹生成，如下圖：

3）再對葉子進行編碼，從上到下，所有左鏈結0，右連結為1。結果如下圖：
故字串”alibaba“佔用的編碼空間為：1*3+2*2+（3+3）*1=13（bit）。

6、樹的孩子-兄弟連結串列儲存方式（樹轉化為二叉樹的方法）和  二叉樹轉化為森林

答：（1）孩子-兄弟連結串列儲存方式是左指標指向孩子鏈，右指標指向兄弟鏈。這樣就可以將普通樹結構轉化為二叉樹結構，經過此轉化後，原樹的後序遍歷變為二叉樹的中序遍歷，前序遍歷依然是前序遍歷（注意：樹是沒有中序遍歷的，二叉樹才有中序遍歷）。

例如：

注意：樹變成二叉樹的情況下，

根節點無右兄弟，右指標域一定為空；  -----------------1個 
除根節點之外的每個非終端節點都有孩子，其下的分支一定有最終的葉子節點，右指標域為空；-----------------n-1個 
其中最後一個非終端節點無右兄弟，右指標域也為空。-------------------加1個 
因此，若樹有N個非終端結點，那麼右指標為空的結點共有n+1個。

（2）二叉樹轉化為森林正好與森林轉化為二叉樹相反，即：將二叉樹結點的左孩子保留，右孩子變為結點的兄弟。

五、圖

1、圖的相關基礎知識

答：由頂點和邊構成圖，根據邊是否有向分為有向圖和無向圖，有向圖記為G1=（V1，{A1}），無向圖記為G2=（V2{E2}）。邊較少的稱為稀疏圖，反之稠密圖。
路徑：無向圖中從頂點v到v'稱為路徑； 簡單路徑：路徑中所有頂點不重複出現的稱為; 關鍵路徑：從源點到匯點的路徑長度最長的路徑叫關鍵路徑；第一和最後頂點相同的路徑稱為環，除了第一和最後頂點外，其餘頂點不重複出現的稱為簡單環。 連通分量：連通分量是指無向圖中的極大連通子圖；有向圖中的極大強連通子圖稱做有向圖的強連通分量。 有向完全圖：有向完全圖是指圖中各邊都有方向，且每兩個頂點之間都有兩條方向相反的邊連線的圖。故n個頂點的有向完全圖有n(n-1)條邊。
圖的儲存：可以用鄰接矩陣、鄰接表、十字連結串列、鄰接多重表儲存。鄰接矩陣：為方陣，階數等於頂點數，矩陣元素就是邊的權值（若兩點無連線則權值為無窮大），元素所在行列則為邊兩端的頂點。注意：無向圖的鄰接矩陣具有對稱性，所以一般採用壓縮模式，只填寫矩陣上三角或下三角。（可見，鄰接矩陣大小隻和圖的頂點數有關）鄰接表：圖的每一個頂點都建立一個單鏈表，該連結串列中的每個結點是以該頂點為尾的邊（無向圖則為依附於該頂點的邊）。故同頂點數的有向圖的鄰接表結點數是無向圖一半。 有向圖的拓撲排序：
（1）從圖中找到無前驅的頂點輸出；
（2）刪除該頂點及以其為尾弧；
（3）重複（1）（2），直至刪完所有頂點。

2、圖的遍歷：

答：（1）深度優先搜尋：類似樹的先根遍歷；（用棧作為輔助資料結構，這是根據結點遍歷順序決定的）
（2）廣度優先搜尋：類似樹的按層搜尋。（用佇列作為輔助資料結構，這是根據結點遍歷順序決定的）
廣度優先搜尋（BFS）是最適合解決無權值或權值相等的單源最短路徑問題的。無權值或權值相等的單源最短路徑是指：從圖中某一點作為頂點出發，向終點搜尋，找到最短的一條路徑。

深度優先遍歷圖的方法是，從圖中某頂點v出發：

①訪問頂點v;
②依次從v的未被訪問的鄰接點（任何一個鄰接點即可，不一定是深度最大的那個鄰接點）出發，對圖進行深度優先遍歷;直至圖中和v有路徑相通的頂點都被訪問;
③若此時圖中尚有頂點未被訪問，則從一個未被訪問的頂點出發，重新進行深度優先遍歷，直到圖中所有頂點均被訪問過為止。

（3）BFS和DFS生成樹演算法 ①根據深度優先遍歷思想，BFS生成樹演算法所生成的樹高是要小於或等於DFS演算法省的樹高； ②有向環的判斷方式： 拓撲排序（找不到無前驅，但頂點未刪完，表示有環）；
深度優先排序（找到重複訪問的頂點表示有環）。

有人說還有”最短路徑“，我不太明白。

3、圖的尤拉路與歐拉回路

答：如下： （1）尤拉路
圖G存在一條路，經過G中每條邊有且僅有一次，稱這條路為尤拉路；
判斷條件：
有向圖：圖連通，有一個頂點：出度-入度=1，有一個頂點：入度-出度=1，其餘都是出度=入度。出度-入度=1的點做起點，入度-出度=1的點做終點；
無向圖：圖連通，只有兩個頂點是奇數度，其餘都是偶數度的。起點必須是奇數度點；
（2）歐拉回路
如果圖G存在一條迴路，經過G每條邊有且僅有一次，稱這條迴路為歐拉回路。
判斷條件：
有向圖：圖連通，所有的頂點出度=入度。
無向圖：圖連通，所有頂點都是偶數度。

4、圖在含有共享子式的表示式中應用：

答：圖在這種表示式中的應用可以避免二叉樹表示的表示式不能對共享子式的記憶體重用。
首先介紹二叉樹表示式：(a+b)*(b*(c+d)+(c+d)*e)*((c+d)*e

即：按表示式順序設定結點，父節點用作符號位，葉子結點用作資料位（左葉子用作左運算元，右葉子用作右運算元），結果傳到父節點。然後介紹圖對該表示式的表示：

與二叉樹表示式對比，即：將重複的結點去掉，有向弧重新連線。故圖對錶達式的表示中：結點數=去除重複後運算元+符號數（不去重複）。

5、圖表示的事件與活動之最早、最遲發生/開始時間

答：如圖：

圖中節點代表事件，邊代表活動（注意無向圖中邊都是從左-> 右， 即 a3 對應的是 <B,D> B->D 這個方向）；

事件是瞬間發生就結束，活動發生後要持續一段時間；

（1）事件發生時間

事件 D 的最早發生時間： 
從源點 A 開始到達 D 的所有路徑加和的最大值 max{<a1,a3>,<a2,a5>} = 6；事件 D 的最遲發生時間 ：  
首先求出匯點 F  的最早發生時間 max{<a1,a4,a8>,<a1,a3,a7>,<a2,a5,a7>,<a2,a6>} = 8
匯點 F 的最早發生時間 - max{匯點逆向到事件 D 的路徑累加之和} = 8- max{<a7>} = 5；

（2）活動發生時間

活動a3的最早發生時間：
以 a3 該活動為出發點的事件 
B---a3--->D ， 即， B 事件的最早發生時間； 活動a3的最遲發生時間： 
以a3 該活動對應的箭頭所指向的事件的最遲發生時間 - a3 活動持續時間 
B---a3--->D ， 即， D 事件的最遲發生時間 - a3 活動的持續時間 = 5 - 2 = 3 。

綜上所述，無論事件還是活動：
最早發生時間，事件=活動，是從前往後計算；
最遲發生時間，都是從後往前計算（活動最遲發生時間與活動持續時間有關）。

（3）補充：

AOE網( Activity On Edge Network )： 在帶權有向無環圖中，以頂點表示事件，有向邊表示活動，邊上的權值表示該活動持續的時間（上述例子就是AOE）；

AOV網( Activity On Vertex Network )： 在有向圖中若以頂點表示活動，有向邊表示活動之間的先後關係。

6、求圖的最短路徑——迪傑斯特拉演算法與弗洛伊德演算法

答：（1）迪傑斯特拉演算法

①迪傑斯特拉演算法是典型的單源最短路徑演算法，用於計算圖中一個源節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴充套件，直到擴充套件到終點為止。

②演算法過程：
(a)初始化：用起點v到該頂點w的直接邊(弧)初始化最短路徑，否則設為∞；
(b)從未求得最短路徑的終點中選擇路徑長度最小的終點u：即求得v到u的最短路徑；
(c)修改最短路徑：計算u的鄰接點的最短路徑，若(v,…,u)+(u,w)<(v,…,w)，則以(v,…,u,w)代替；
(d)重複(b)(c)，直到求得v到其餘所有頂點的最短路徑。

③舉例1：

④舉例2：若給出的是鄰接矩陣，那麼應該如下過程：

⑤時間複雜度=O(n^2)；

（2）弗洛伊德演算法

①弗洛伊德演算法是求解圖中任意兩點間的最短路徑的一種演算法，它是一種經典的動態規劃演算法；

②演算法思想：每次從 vi 到 vj 的所有可能存在的路徑中，選出一條長度最短的路徑。一共進行n次；

③時間複雜度=O(n^3)；

7、二分圖以及最大匹配

答：二分圖：

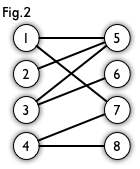
把一個圖的頂點劃分為兩個不相交集 U 和V ，使得每一條邊都分別連線U、 V 集中的頂點。如果存在這樣的劃分，則此圖為一個二分

圖。如圖1就是二分圖，圖2是圖1的規範表現模式。

匹配：

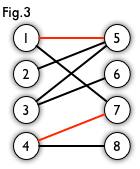
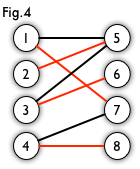
在圖論中，一個匹配（matching）是一個邊的集合，匹配集合中任意兩條邊都沒有公共頂點。例如，圖3、圖4 中紅色的邊就是圖2 的匹配。

最大匹配：一個圖所有匹配中，所含匹配邊數最多的匹配，稱為這個圖的最大匹配。圖 4 是一個最大匹配，它包含 4 條匹配邊。

六、查詢

1、查詢及查詢表

答：查詢即從一種資料儲存容器中查詢到指定資料，需要使用的資料結構稱為查詢表，查詢表分為：靜態查詢表和動態查詢表；

（1）靜態查詢表：表固定，只用於查詢元素資訊。如順序表（折半查詢）、靜態二叉樹等；

（2）動態查詢表：不僅用於查詢元素，還有元素插入與刪除，插入刪除後查詢表資料結構要進行調整。如二叉排序樹、平衡二叉樹、B樹和B+樹等；

2、最小堆（小根堆）與最大堆（大根堆）

答：堆是一種經過排序的完全二叉樹。
n個元素的序列{k1,k2,…,kn}，當且僅當滿足如下關係時被成為堆；

 (1)Ki <= k2i 且 ki <= k2i+1 ；

 (2) Ki >= k2i 且 ki >= k2i+1 ；(i = 1,2,…[n/2])

當滿足(1)時為最小堆，當滿足(2)時為最大堆。

注意：優先佇列實質就是最大/最小堆，最大優先佇列就是大根堆實現的，最小優先佇列就是小根堆實現的。

用二叉樹表示就是：二叉樹的父節點總是大於或小於任一子節點。

將陣列轉化為堆二叉樹的過程叫“堆化樹”，如下：

先按陣列順序一層層填從二叉樹，然後從最底層開始與父節點交換不符合堆規定的結點。

堆的插入與刪除：

①C++的STL中有大根堆和小根堆的實現：

priority_queue<int> qmax;//預設大根堆
priority_queue<int,vector<int>,greater<int>> qmin;//小根堆

上述插入、刪除、讀取堆頂元素分別使用：qmin.push(num)、qmin.pop()、num=qmin.top()函式，插入或刪除元素後自動進行堆調整。

②除上述優先隊列表示大根堆、小根堆外，還可以直接使用make_heap函式直接將vector構造成堆，只是這樣每次插入刪除後需要程式設計師自己重新呼叫make_heap函式調整堆結構。如下：

vector<int> v;//用於建堆的陣列
make_heap(v.begin(),v.end());//建堆，預設最大堆，要建立最小堆可以新增第三個引數greater<int>() 
v.push_back(input);  //插入元素到陣列尾部
make_heap(v.begin(),v.end());       //調整堆
v.pop_back();  //彈出陣列末尾元素
make_heap(v.begin(),v.end());//調整堆

3、二叉排序樹（又叫二叉搜尋樹或二叉查詢樹）

答：（1）二叉排序樹： 首先不一定是完全二叉樹，或者是一棵空樹；或者是具有下列性質的二叉樹： ①若左子樹不空，則左子樹上所有結點的值均小於它的根結點的值； ②若右子樹不空，則右子樹上所有結點的值均大於它的根結點的值； ③左、右子樹也分別為二叉排序樹； ④對任意點，它的左子樹的元素全部小於它，右子樹的所有元素全部大於它； 二叉排序樹查詢法：查詢一個元素x，從根節點開始，若x小於根結點，則到左子樹繼續查詢，否則到右子樹，以此類推；

（2）二叉排序樹的ASL是什麼？

ASL就是平均查詢長度。

ASL =∑PiCi（Pi 為查詢第i個記錄的概率，Ci為找到第i個記錄資料需要比較的次數，Ci隨查詢過程的不同而不同。

1）滿二叉樹時，若每個記錄的查詢概率相等時，Pi =1/n；ASL = 1/n（1*20+2*21+.....+n*2n-1）=log2（n+1）-1；

2）要求查詢成功的ASL最大，就是隻有左子樹或者只有右子樹的情況，即順序表以第一個數或最後一個數為根節點作二叉排序樹。同樣，若每個記錄的查詢概率相等時，Pi =1/n。∑PiCi=1/n∑(n-i+1)=(n+1)/2。

（3）採用插入結點法將一資料序列生成二叉排序樹的方法：
第一個資料做根節點，第二個資料與根節點比較，小於則放左孩子結點，大於則右孩子結點；第三個資料再與根節點比較，小於則表示屬於左子樹，若左子樹已有結點，則像與根節點比較方式一樣與左子樹根節點比較及插入，大於則屬於右子樹，插入方式同左子樹；第四個資料……，方法同上，直至插入完成。例如，資料元素為(34,76,45,18,26,54,92,65),按照依次插入節點的方法生成一棵二叉排序樹為：

4、二叉平衡樹

答：二叉平衡樹（AVL樹）：或者是一顆空樹，或者具有以下性質的二叉樹：它的左子樹和右子樹的深度之差的絕對值不超過1，且它的左子樹和右子樹都是一顆平衡二叉樹。 （1）平衡因子(bf)：結點的左子樹的深度減去右子樹的深度，那麼顯然-1<=bf<=1；很顯然，平衡二叉樹是在二叉排序樹(BST)上引入的，就是為了解決二叉排序樹的不平衡性導致時間複雜度大大下降，那麼AVL就保持住了(BST)的最好時間複雜度O(logn)。但是其每次的插入和刪除都要確保二叉樹的平衡，所以造成了插入和刪除運算的複雜化。 （2）二叉平衡樹的插入：插入根節點後，不平衡就用旋轉來轉化為平衡。如下四種情況： 右旋: 在最小平衡子樹根節點平衡因子>=2且在根節點的左孩子的左孩子插入元素，進行右旋； 左旋: 在最小平衡子樹根節點平衡因子>=-2且在根節點的右孩子的右孩子插入元素，進行左旋；
右旋左旋：最小平衡子樹根節點的右孩子的左孩子的子節點插入新元素，先繞根節點的右孩子節點右旋，再圍根節點左旋；
左旋右旋：最小平衡子樹根節點的左孩子的右孩子的子節點插入新元素，先繞根節點的左孩子節點右旋，再圍根節點左旋。
具體方式圖解：http://www.cnblogs.com/guyan/archive/2012/09/03/2668399.html
（3）這裡有兩點要注意： ①如果根結點和其子節點都不平衡，先旋轉子節點使子樹先平衡，如下圖(a)； ②旋轉後，某結點的度大於2，需要將其拆下用於補齊下一層的，補齊左子樹還是右子樹需要根據其值大小與根節點的比值確定。

5、B樹（或叫B-樹）

答：（1）B樹： B樹是一種多路平衡樹或叫做一種平衡的多路搜尋樹，其相比二叉搜尋樹（後面叫做BST）區別： ①BST每個節點只有1個關鍵字，所以每個節點最多隻有2叉；而B樹每個節點最多有m-1個關鍵字，所以最多可有m叉； ②BST的葉子結點可在不同層，即使是二叉平衡樹也可在不同層；而B樹所有葉子結點都在最底下同一層。 注意：B樹和B-樹是一個東西，英文都是B-Tree，翻譯過來保留-就是B-樹，否則就是B樹； （2）一棵m階的B樹滿足下列條件（這裡的m階是指樹中每個節點最多含有m個子樹）： ①若根結點不是葉子結點，則至少有2個孩子；
② 除根結點和葉子結點外，其它每個結點至少有ceil(m/2)個孩子，至多有m個孩子；
③所有葉子結點都出現在同一層（這是與多路排序樹或者多路平衡樹不同的地方）；
④每個結點存放至少M/2-1（取上整）和至多M-1個關鍵字；
⑤非葉子結點包含有兒子數-1個關鍵字；
⑥非葉子結點的關鍵字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；
⑦非葉子結點的指標：P[1], P[2], …, P[M]；其中P[1]指向關鍵字小於K[1]的子樹，P[M]指向關鍵字大於K[M-1]的子樹，其它P[i]指向關鍵字屬於(K[i-1], K[i])的子樹； （3）補充：B樹是多路（叉）平衡樹或者說平衡的多路（叉）排序樹，並不代表多路平衡樹就是B樹。因為多路平衡樹無法保證葉子結點都在同一層。 （4）分裂的方法： ①在插入時，結點關鍵字個數超標，則生成一新結點。把原結點上的關鍵字和k按升序排序後，從中間位置把關鍵字（不包括中間位置的關鍵字）分成 兩部分。 ②左部分所含關鍵字放在舊結點中，右部分所含關鍵字放在新結點中，中間位置的關鍵字連同新結點的儲存位置插入到父結點中。 ③如果父結點的關鍵字個數也超過（m-1），則要再分裂，再往上插。直至這個過程傳到根結點為止。
插入時分裂方法如下：

（5）刪除方法： ①被刪關鍵字Ki所在結點的關鍵字數目不小於ceil(m/2)，則只需從結點中刪除Ki和相應指標Ai，樹的其它部分不變。

②被刪關鍵字Ki所在結點的關鍵字數目等於ceil(m/2)-1，則需調整。調整過程如上面所述。

③被刪關鍵字Ki所在結點和其相鄰兄弟結點中的的關鍵字數目均等於ceil(m/2)-1，假設該結點有右兄弟，且其右兄弟結點地址由其雙親結點指標Ai所指。則在刪除關鍵字後，它所在結點的剩餘關鍵字和指標，加上雙親結點中的關鍵字Ki一起，合併到Ai所指兄弟結點中。

6、B+ 樹和B*樹

答：B+ 樹的+後面要空一格，英文名為B+ Tree；

（1）B+樹是B樹的一種變形樹，它與B樹的差異在於：

①非葉子結點僅僅儲存索引並用於指向分支，實際資料都存放在葉子結點中，並且有一個鏈頭在樹結構外的連結串列將所有的葉子結點連結在一起；

②由①，一個節點有m各分支，該節點就有m個關鍵字，即有k個子分支的結點必然有k個關鍵字；

（2）B*樹是B+樹的變形，在B+樹基礎上將每層非葉子結點層也用一個連結串列連結起來；

（2）總結B樹和B+ 樹：

①概括：B樹是葉節點在同一層的多叉排序樹，B+ 是在B樹基礎上將非葉節點改為用於儲存指向子節點指標索引的多路平衡樹（葉節點也在同一層）；

②為什麼要B樹？在磁碟讀寫過程中，磁碟尋道（或叫做磁碟定位）是一個非常花費時間的過程，B樹作用就是對磁碟儲存結構進行優化，提高磁碟讀取時定位的效率。

③為什麼要B+ 樹？由於B+樹的分支結點均為索引且資料都儲存在葉子結點中，葉子節點形成了一個有序的連結串列。所以B+ 樹適合掃庫，只需要掃一遍葉子結點就可進行掃庫。

④通常B和B+樹用於資料庫索引，B一般適合資料庫的磁碟節點查詢，B+樹適合資料庫分段範圍內查詢以及插入刪除操作，而hash_map適合記憶體

查詢；

⑤B*樹：在B+樹基礎上，為非葉子結點也增加連結串列指標，將結點的最低利用率從1/2提高到2/3；

7、紅黑樹以及其查詢複雜度

相關推薦