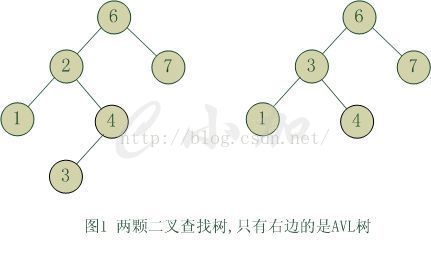
平衡二叉樹（Balanced Binary Tree）是二叉查詢樹的一個進化體，也是第一個引入平衡概念的二叉樹。1962年，G.M. Adelson-Velsky 和 E.M. Landis發明了這棵樹，所以它又叫AVL樹。平衡二叉樹要求對於每一個節點來說，它的左右子樹的高度之差不能超過1，如果插入或者刪除一個節點使得高度之差大於1，就要進行節點之間的旋轉，將二叉樹重新維持在一個平衡狀態。這個方案很好的解決了二叉查詢樹退化成連結串列的問題，把插入，查詢，刪除的時間複雜度最好情況和最壞情況都維持在O(logN)。但是頻繁旋轉會使插入和刪除犧牲掉O(logN)左右的時間，不過相對二叉查詢樹來說，時間上穩定了很多。

平衡二叉樹實現的大部分過程和二叉查詢樹是一樣的（學平衡二叉樹之前一定要會二叉查詢樹），區別就在於插入和刪除之後要寫一個旋轉演算法去維持平衡，維持平衡需要藉助一個節點高度的屬性。我參考了機械工業出版社的《資料結構與演算法分析-C語言描述》寫了一個C++版的程式碼。這本書的AVLTree講的很好，不過沒有很完整的去描述。我會一步一步的講解如何寫平衡二叉樹，重點是平衡二叉樹的核心部分，也就是旋轉演算法。

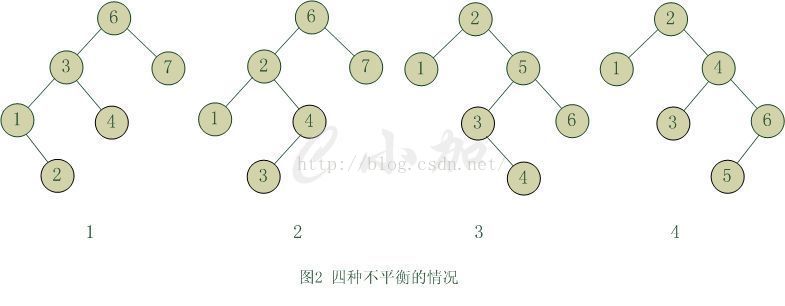
四種不平衡的情況：

      1、6節點的左子樹3節點高度比右子樹7節點大2，左子樹3節點的左子樹1節點高度大於右子樹4節點，這種情況成為左左。

　　2、6節點的左子樹2節點高度比右子樹7節點大2，左子樹2節點的左子樹1節點高度小於右子樹4節點，這種情況成為左右

　　3、2節點的左子樹1節點高度比右子樹5節點小2，右子樹5節點的左子樹3節點高度大於右子樹6節點，這種情況成為右左。

　　4、2節點的左子樹1節點高度比右子樹4節點小2，右子樹4節點的左子樹3節點高度小於右子樹6節點，這種情況成為右右。

　　從圖2中可以可以看出，1和4兩種情況是對稱的，這兩種情況的旋轉演算法是一致的，只需要經過一次旋轉就可以達到目標，我們稱之為單旋轉。2和3兩種情況也是對稱的，這兩種情況的旋轉演算法也是一致的，需要進行兩次旋轉，我們稱之為雙旋轉。

左左和右右的旋轉方式對稱，且都只需要一次旋轉就能恢復平衡。

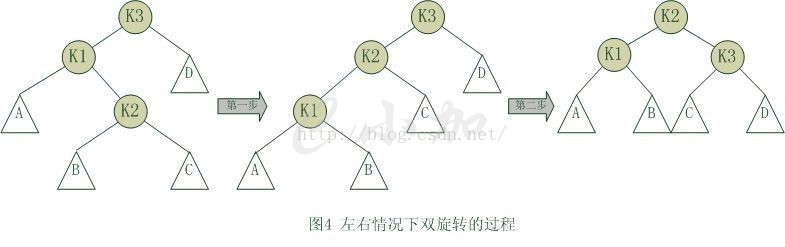
雙選裝：

對於左右和右左這兩種情況，單旋轉不能使它達到一個平衡狀態，要經過兩次旋轉。