0. 資料結構圖文解析系列

1. 二叉堆的定義

二叉堆是一種特殊的堆，二叉堆是完全二叉樹或近似完全二叉樹。二叉堆滿足堆特性：父節點的鍵值總是保持固定的序關係於任何一個子節點的鍵值，且每個節點的左子樹和右子樹都是一個二叉堆。
當父節點的鍵值總是大於或等於任何一個子節點的鍵值時為最大堆。 當父節點的鍵值總是小於或等於任何一個子節點的鍵值時為最小堆。

2. 二叉堆的儲存

二叉堆一般使用陣列來表示。請回憶一下二叉樹的性質，其中有一條性質：

性質五：如果對一棵有n個節點的完全二叉樹的節點按層序編號（從第一層開始到最下一層，每一層從左到右編號，從1開始編號），對任一節點i有：

1. 如果i=1 ，則節點為根節點，沒有雙親。
2. 如果2 * i > n ，則節點i沒有左孩子 ；否則其左孩子節點為2*i . （n為節點總數）
3. 如果2 * i+1>n ，則節點i沒有右孩子；否則其右孩子節點為2*1+1.

簡單來說：

1. 如果根節點在陣列中的位置是1，第n個位置的子節點分別在2n 與 2n+1，第n個位置的雙親節點分別在⌊i /2⌋。因此，第1個位置的子節點在2和3.
2. 如果根節點在陣列中的位置是0，第n個位置的子節點分別在2n+1與2n+2，第n個位置的雙親節點分別在⌊（i-1） /2⌋。因此，第0個位置的子節點在1和2.

得益於陣列的隨機儲存能力，我們能夠很快確定堆中節點的父節點與子節點。

下面以大頂堆展示一下堆的陣列儲存。

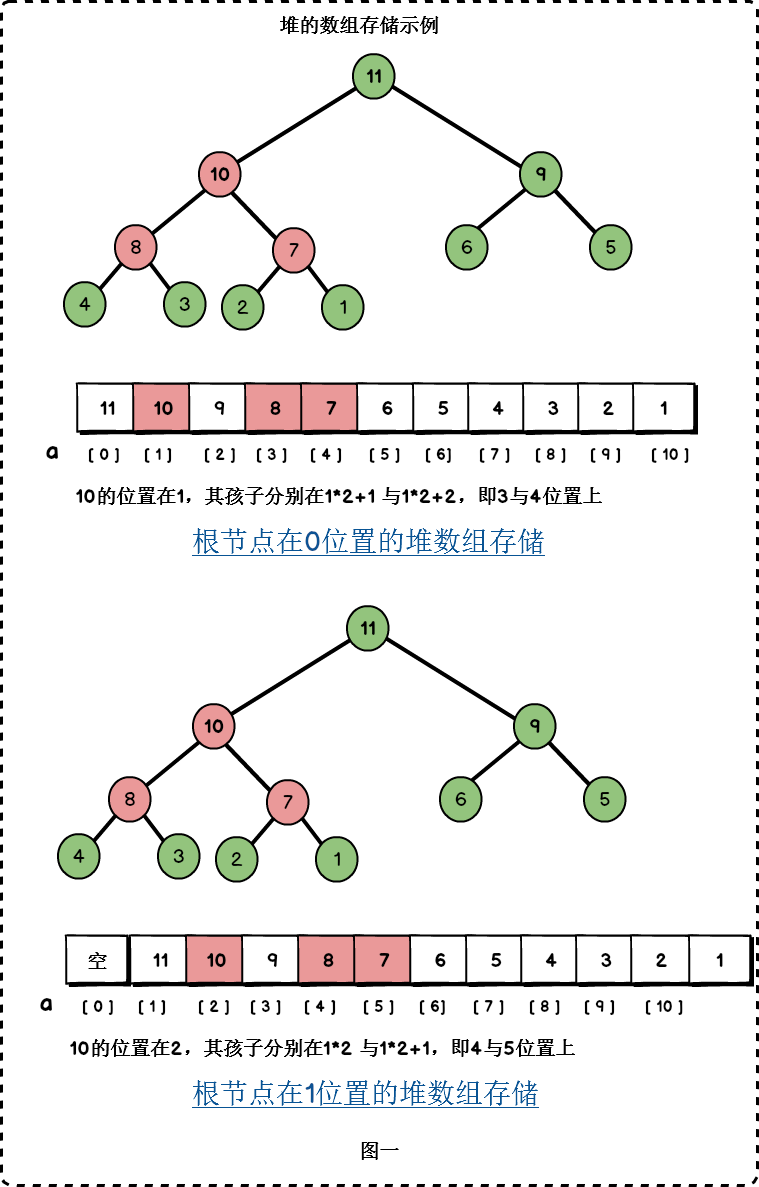
在本文中，我們以大頂堆為例進行堆的講解。本文大頂堆的根節點位置為0.

3. 二叉堆的具體實現

在二叉堆上可以進行插入節點、刪除節點、取出堆頂元素等操作。

3.1 二叉堆的抽象資料型別

/*大頂堆類定義*/
template <typename T>
class MaxHeap
{
public:
    bool insert(T val);     //往二叉堆中插入元素
    bool remove(T data);    //移除元素
    void print();           //列印堆
    T getTop();             //獲取堆頂元素
    bool createMaxHeap(T a[], int size);//根據指定的陣列來建立一個最大堆

    MaxHeap(int cap = 10);
    ~MaxHeap();

private:
    int capacity;   //容量，也即是陣列的大小
    int size;       //堆大小，也即是陣列中有效元素的個數
    T * heap;       //底層的陣列
private:
    void filterUp(int index); //從index所在節點，往根節點調整堆
    void filterDown(int begin ,int end ); //從begin所在節點開始，向end方向調整堆
};
 

1. 注意capacity與size的區別。capacity指的是陣列的固有大小。size值陣列中有效元素的個數，有效元素為組成堆的元素。
2. heap為陣列。

3.2 二叉堆的插入

在陣列的最末尾插入新節點，然後自下而上地調整子節點與父節點的位置：比較當前結點與父節點的大小，若不滿足大頂堆的性質，則交換兩節點，從而使當前子樹滿足二叉堆的性質。時間複雜度為O(logn)。
當我們在上圖的堆中插入元素12：

調整過程：

1. 節點12新增在陣列尾部，位置為11；
2. 節點12的雙親位置為⌊11/2⌋ = 5，即節點6；節點12比節點6大，與節點6交換位置。交換後節點12的位置為5.
3. 節點12的雙親位置為⌊ 5 /2⌋ = 2,即節點9；節點12比節點9大，與節點9交換位置。交換後節點12的位置為2.
4. 節點12的雙親位置為⌊2/2⌋ = 1，即節點11；節點12比節點11大，與節點11交換位置。交換後節點12的位置為1.
5. 12已經到達根節點，調整過程結束。

這個從下到上的調整過程為：

/*從下到上調整堆*/
/*插入元素時候使用*/
template <typename T>
void MaxHeap<T>::filterUp(int index)
{
    T value = heap[index];  //插入節點的值，圖中的12

    while (index > 0) //如果還未到達根節點，繼續調整
    {
        int indexParent = (index -1)/ 2;  //求其雙親節點
        if (value< heap[indexParent])
            break;
        else 
        {
            heap[index] = heap[indexParent];
            index = indexParent;
        }
    }
    heap[index] = value;    //12插入最後的位置
};

在真正程式設計的時候，為了效率我們不必進行節點的交換，直接用父節點的值覆蓋子節點。最後把新節點插入它最後的位置即可。

基於這個調整函式，我們的插入函式為：

/*插入元素*/
template <typename T>
bool MaxHeap<T>::insert(T val)
{
    if (size == capacity) //如果陣列已滿，則返回false
        return false;
    heap[size] = val;
    filterUp(size);
    size++;
    return true;
};

3.3 二叉堆的刪除

堆的刪除是這樣一個過程：用陣列最末尾節點覆蓋被刪節點，再從該節點從上到下調整二叉堆。我們刪除根節點12：

可能有人疑惑，刪除後陣列最末尾不是多了一個6嗎？
的確，但我們把陣列中有效元素的個數減少了一，最末尾的6並不是堆的組成元素。

這個從上到下的調整過程為：

/*從上到下調整堆*/
/*刪除元素時候使用*/
template<typename T>
void MaxHeap<T>::filterDown(int current,int end)
{

    int child = current * 2 + 1; //當前結點的左孩子

    T value = heap[current];    //儲存當前結點的值

    while (child <= end)
    {
        if (child < end && heap[child] < heap[child+1])//選出兩個孩子中較大的孩子
            child++;
        if (value>heap[child])  //無須調整；調整結束
            break;
        else
        {
            heap[current] = heap[child];    //孩子節點覆蓋當前結點
            current = child;                //向下移動
            child = child * 2 + 1;          
        }
    }
    heap[current] = value;
};

基於調整函式的刪除函式：

/*刪除元素*/
template<typename T>
bool MaxHeap<T>::remove(T data)
{
    if (size == 0) //如果堆是空的
        return false;
    int index;
    for (index = 0; index < size; index++)  //獲取值在陣列中的索引
    {
        if (heap[index] == data)
            break;
    }
    if (index == size)            //陣列中沒有該值
        return false; 
 
    heap[index] = heap[size - 1]; //使用最後一個節點來代替當前結點，然後再向下調整當前結點。
 
    filterDown(index,size--);  
 
    return true;
};

3.4 其餘操作

其餘操作很簡單，不在這裡囉嗦。

/*列印大頂堆*/
template <typename T>
void MaxHeap<T>::print()
{
    for (int i = 0; i < size; i++)
        cout << heap[i] << " ";
};
/*獲取堆頂元素*/
template <typename T>
T MaxHeap<T>::getTop()
{
    if (size != 0)
        return heap[0];
};

/*根據指定的陣列來建立一個最大堆*/
template<typename T>
bool MaxHeap<T>::createMapHeap(T a[], int size)
{
    if (size > capacity)    //  堆的容量不足以建立
        return false;
    for (int i = 0; i < size; i++)
    {
        insert(a[i]);
    }
    return true;
};

4. 二叉堆程式碼測試

測試程式碼：

int _tmain(int argc, _TCHAR* argv[])
{
    MaxHeap<int> heap(11);
    //逐個元素構建大頂堆
    for (int i = 0; i < 10; i++)
    {
        heap.insert(i);
    }
    heap.print();
    cout << endl;
    heap.remove(8);
    heap.print();
    cout << endl;

    //根據指定的陣列建立大頂堆
    MaxHeap<int> heap2(11);
    int a[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
    heap2.createMaxHeap(a, 10);
    heap2.print();
    getchar();
    return 0;
}

執行結果：

9 8 5 6 7 1 4 0 3 2
9 7 5 6 2 1 4 0 3
10 9 6 7 8 2 5 1 4 3

5. 大頂堆、小頂堆完整程式碼下載