Heap排序法演算法分析

選擇排序法的概念簡單，每次從未排序部份選一最小值，插入已排序部份的後端，其時間主要花費於在整個未排序部份尋找最小值，如果能讓搜尋最小值的方式加 快，選擇排序法的速率也就可以加快，Heap排序法讓搜尋的路徑由樹根至最後一個樹葉，而不是整個未排序部份，因而稱之為改良的選擇排序法。

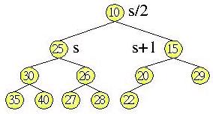
Heap排序法使用Heap Tree（堆積樹），樹是一種資料結構，而堆積樹是一個二元樹，也就是每一個父節點最多隻有兩個子節點（關於樹的詳細定義還請見資料結構書籍），堆積樹的 父節點若小於子節點，則稱之為最小堆積（Min Heap），父節點若大於子節點，則稱之為最大堆積（Max Heap），而同一層的子節點則無需理會其大小關係，例如下面就是一個堆積樹： 

可以使用一維陣列來儲存堆積樹的所有元素與其順序，為了計算方便，使用的起始索引是1而不是0，索引1是樹根位置，如果左子節點儲存在陣列中的索引為s，則其父節點的索引為s/2，而右子節點為s+1，就如上圖所示，將上圖的堆積樹轉換為一維陣列之後如下所示：

首先必須知道如何建立堆積樹，加至堆積樹的元素會先放置在最後一個樹葉節點位置，然後檢查父節點是否小於子節點（最小堆積），將小的元素不斷與父節點交換，直到滿足堆積樹的條件為止，例如在上圖的堆積加入一個元素12，則堆積樹的調整方式如下所示：

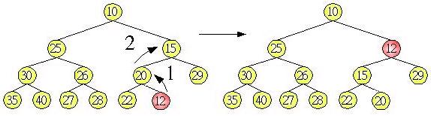
建立好堆積樹之後，樹根一定是所有元素的最小值，您的目的就是：

將最小值取出

然後調整樹為堆積樹

不斷重複以上的步驟，就可以達到排序的效果，最小值的取出方式是將樹根與最後一個樹葉節點交換，然後切下樹葉節點，重新調整樹為堆積樹，如下所示：

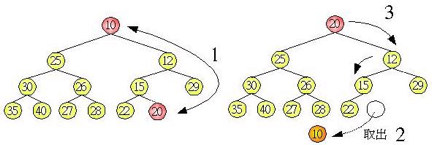
調整完畢後，樹根節點又是最小值了，於是我們可以重覆這個步驟，再取出最小值，並調整樹為堆積樹，如下所示：

如此重覆步驟之後，由於使用一維陣列來儲存堆積樹，每一次將樹葉與樹根交換的動作就是將最小值放至後端的陣列，所以最後陣列就是變為已排序的狀態。

其實堆積在調整的過程中，就是一個選擇的行為，每次將最小值選至樹根，而選擇的路徑並不是所有的元素，而是由樹根至樹葉的路徑，因而可以加快選擇的過程， 所以Heap排序法才會被稱之為改良的選擇排序法。

程式碼實現（C/OC）

#define MAX 10
#define SWAP(x,y) {int t; t = x; x = y; y = t;}

void createheap(int[]);
void heapsortt(int[]);
 

//主程式（C/OC）
int number[MAX+1] = {-1};
int i, num;

srand(time(NULL));

printf("排序前：");
for(i = 1; i <= MAX; i++) {     //生成排序前的陣列
    number[i] = rand() % 100;
    printf("%d ", number[i]);
}

printf("\n建立堆積樹：");
createheap(number);             //建立堆積樹
for(i = 1; i <= MAX; i++)       //列印堆積樹
    printf("%d ", number[i]);
printf("\n");

heapsortt(number);              //利用堆積樹進行選擇排序
printf("\n");

//建立堆積樹
void createheap(int number[]) {     
    int i, s, p;
    int heap[MAX+1] = {-1};         //臨時陣列
    
    for(i = 1; i <= MAX; i++) {     //依次排列堆積樹中的每個元素的值，i為多少，就排第幾個
        heap[i] = number[i];
        s = i;
        p = i / 2;                  //除以2，正好可以獲得父節點的下標
        while(s >= 2 && heap[p] > heap[s]) {//如果父節點大於子節點的值，交換
            SWAP(heap[p], heap[s]);
            s = p;
            p = s / 2;
        }
    }
    
    for(i = 1; i <= MAX; i++)       //賦值
        number[i] = heap[i];
}

//選擇排序
void heapsortt(int number[]) {      
    int i, m, p, s;
    
    m = MAX;
    while(m > 1) {
        SWAP(number[1], number[m]);         //交換堆積樹的首尾節點的值
        m--;
        
        p = 1;                              //父節點以頂點開始
        s = 2 * p;                          //指向左子節點
        
        while(s <= m) {
            if(s < m && number[s+1] < number[s])//兩個子節點進行比較，右子節點較小，s指向兩個中最小的子節點
                s++;
            if(number[p] <= number[s])          //父節點更小，而且因為之前為最小堆積樹，所以跳出
                break;
            SWAP(number[p], number[s]);         //沒有跳出，交換較小子節點與父節點
            p = s;                              //p指向新的父節點
            s = 2 * p;                          //s指向新的子節點
        }
        
        printf("\n排序中：");
        for(i = MAX; i > 0; i--)                //最小值已經放到較大下標處（已在堆積樹外），故倒序列印
            printf("%d ", number[i]);
    } 
}