演算法分析神器—時間複雜度
時間複雜度是學習演算法的基石,今天我們來聊聊為什麼要引入時間複雜度,什麼是時間複雜度以及如何去算一個演算法的時間複雜度
刻畫演算法的執行時間
某日,克叫來了慧子打算給他補習補習一下基礎知識,只見克寫了一段非常簡單的程式碼


克
你說一下這段程式碼會執行多長時間
這個...,得在計算機上跑一下才可以知道吧

慧子

克
恩恩,對的,那如果我改變n的大小為10000,你能夠預測它的執行時間嗎?
這個...,要不再測一次

慧子

克面無表情

克
我們要善於發現事物的內在規律
克看了一下慧子
這個程式的內在規律是什麼呢?

慧子
慧子看老師有點生氣,開始虛心請教了

克
你要預測當n=10000的時候,這個程式會執行多長時間,你首先要知道程式的執行時間都花在哪了?


克
當電腦執行這段程式碼的時候,執行任何一條語句都需要花費時間,這是時間花費的主要地方
為了方便討論,這裡我們把每一條語句的執行時間都看做是一樣的,記為一個時間單元

克
你看一下剛才的程式都有哪些語句


克
你看,這個程式有這麼幾個地方消耗了時間
① 藍色框的兩條語句,花費兩個時間單元
②黑色框的一條語句,花費n+1個時間單元
③紅色框的兩條語句,花費2*n個時間單元

克
那麼一共花費了3n+3個時間單元,可以看出,程式消耗的時間和你的n成線性關係
這不是數學嗎,慧子心裡想到

克
現在我用T(n)表示這個程式運行了多長時間,那麼這個程式執行的時間就可以寫成T(n)=3n+3
其中的n被我們稱為問題的規模,其實就是你處理問題的大小
克順手畫了這個函式的圖
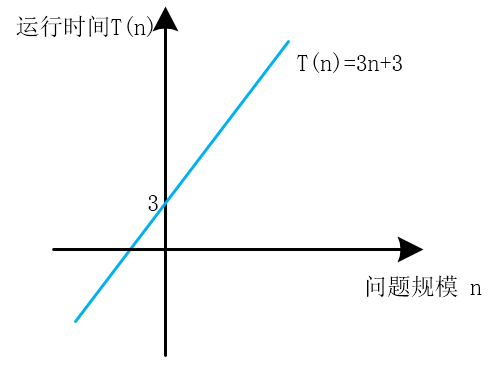
本文主要討論問題規模和執行時間的關係,假定不同輸入和執行時間基本無關
哦,我懂了,要預測程式的時間,我可以把執行時間函式求出來

慧子

克
恩恩,對的
這個函式表示式看起來挺複雜的

慧子

克
我們常常會對這個函式進行簡化,使得它既簡單又不失函式的主要特性
哦?怎麼簡化

慧子
時間複雜度

克
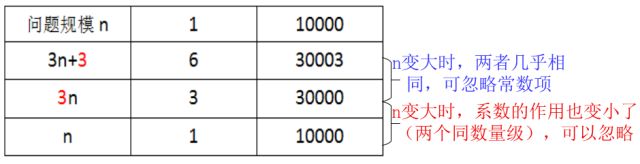
我們一般只關心隨著問題規模n趨於無窮時函式中對函式結果影響最大的項,也就是最高次項
比如說:T(n)=3n+3,當n非常大的時候常數3和n的係數3對函式結果的影響就很小了

克
所以一般我們會保留最高次項並忽略該項的係數
比如: T(n)=n+1忽略常數項 T(n)~n T(n)=n+n^2 忽略低階項 T(n)~n^2
T(n)=3n 忽略最高階的係數 T(n)~n
這個忽略低階項是什麼意思

慧子

克
所謂低階項,簡單地說就是當n非常大時,這個項相對於另外一個項很小,可以忽略,比如n相對於n^2,n就是低階項
哦,我怎麼判斷哪個是高階,哪個是低階呢?

慧子

克
具體要用數學知識,對你而言,你只需記住下面的大小關係就行了,到時按照這個進行忽略(相對較小的忽略)
還好不用掌握那頭疼的數學,慧子心中想到
簡化完了之後呢?

慧子
慧子把話題又拉了回來

克
化簡完後的函式可以近似地代表原來函式的總體趨勢


克
簡化後的式子被稱為這個程式演算法的時間複雜度,記做O(f(n)),f(n)就是簡化後的式子,比如說剛開始討論的T(n)=3n+3,簡化後T(n)~f(n)=n,那我們記為O(n)
更準確地說O代表了執行時間函式的一個漸進上界,即T(n)在數量級上小於等於f(n)
哦,原來時間複雜度可以表示某個演算法的執行時間的趨勢,大致地度量演算法效率的好壞, 那我該如何算這個時間複雜度呢?

慧子
時間複雜度的計算

克
從前面可以總結出計算演算法複雜度大O的方法
一、得出執行時間的函式 二、對函式進行簡化
①用常數1來取代執行時間中所有加法常數
②修改後的函式中,只保留最高階項 ③如果最高階項存在且不是1,則忽略這個項的係數

克
舉個例子吧,先來看這樣一段程式碼


克
顯然,T(n)=3,對這個函式進行簡化,用常數1取代常數3,然後取代後的函式沒有最高階項,那麼這個演算法的時間複雜度就是O(1).
O(1)也被稱為常數階
每次都要把時間函式算出來,好複雜,有沒有簡便一點的方法

慧子

克
這個還真可以耍耍小聰明,一般來說,最內層執行次數最多的語句就決定了整個演算法的趨勢


克
你只要看看最內層的語句執行次數的規律就行了,這個內層列印語句隨著問題規模n的增加會呈線性增加,直接就可以判定複雜度為O(n)
這個方法真棒,那麼按照這個方法就很容易得出下面這個巢狀的兩層for迴圈的複雜度為O(n^2)了

慧子
慧子隨手寫了一段巢狀迴圈的程式碼


克
恩恩,對的,最內層的語句隨n的增加會呈二次函式的規律執行,代表了這個演算法執行時間的一個趨勢
我聽說有一個很神奇的函式叫對數函式,它隨著自變數的增大,因變數增長的很慢,這個應該很受歡迎吧

慧子

克
嗯嗯,對的,對數函式的趨勢顯然比線性函式好(對數函式隨著自變數的增大因變數增長的很慢)

接著,克又寫了一段時間複雜度為對數的程式碼


克
你看,這段程式碼的複雜度就為對數級別的,O(logn)
這個怎麼分析

慧子
一向數學不太好的謙子此時有點懵

克
和之前的分析方法一樣,我們著重看執行次數最多的內層程式碼語句


克
每迴圈一次,sum就給自身乘以2,乘了多少次就跳出迴圈了呢(大於等於n)?不知道,就設為x吧,那麼2^x=n,解出x=logn,這說明隨著n的增大,最消耗時間的內層語句是呈指數變化的
哦,我懂了,原來如此

慧子

克
複雜度的內容很多,你只要理解它的含義以及會分析簡單的演算法就行了,以後遇到複雜的,為師會給你傳授的
好的

慧子
慧子與老師道了別
轉載:
