演算法時間複雜度用來度量演算法執行時間的多少，用大O階表示，即T(n)=O(f(n))，其中n為問題規模，也就是問題的大小。

既然要理解時間複雜度，我們首先理解術語中的兩個關鍵詞——“演算法”和“時間”，理解了它倆就成功一半了。

首先看“演算法”，演算法是解決特定問題的方法，在計算機領域裡需要將演算法用計算機能聽懂的語言描述給它聽，明白之後它才能使用運算能力解決問題。計算機能聽懂的語言，當然是程式程式碼了(還需編譯器將程式碼翻譯成2進位制流)，也就是一系列的指令。

再看“時間”，此處的時間指執行演算法消耗的時間，也就是計算機執行前面所說的一系列指令的時間。這個時間受

• 計算機執行每條指令的速度->硬體層面
• 編譯產生的程式碼質量->軟體層面
• 演算法的好壞(演算法使用的策略)
• 問題規模

的影響。在給定軟硬體環境下，其實就是你在自己電腦上寫演算法的時候，演算法執行時間只受演算法本身的好壞和要處理的問題的規模影響。這樣就將4個影響因素減少為2個，簡化了問題。

既然執行時間受演算法好壞和問題規模n的影響，那麼執行時間就是它倆的函式。

那這個函式到是啥樣的呢？

我們繼續分析，給定問題規模n之後，優秀的演算法可能哐哐哐執行幾次就搞定了，一般的演算法可能吭哧吭哧執行很多很多次才搞定；當給定演算法時，問題規模n很小時，可能執行幾次就搞定，而n很大時，就得執行很多次了。所以演算法優劣和問題規模n改變時，執行次數（基本運算元）將改變，所以執行次數就是演算法優劣和問題規模n的函式。

到此為止，我們得出一個簡單的結論：演算法執行時間可以用執行次數表示。

世界豐富多彩，同一個問題有不同的解決辦法，比如餓了，可以吃米粉也可以吃包子，可以一個人吃也可以一個人吃(hh)。對應演算法領域，同一個問題也可以用不同的演算法解決，既然這樣，那不同的演算法之間肯定有優劣之分，如何評價呢？

最簡單的評價方法是把兩個演算法拉過來比誰解決問題的速度快，誰的執行時間短，誰的執行次數少。

給定演算法時，執行次數變為問題規模n的函式。比如一個演算法是a，一個演算法是b，問題規模為n，那麼執行次數分別為Ca=f(n),Cb=g(n)。現在將比較兩個演算法的執行次數的問題轉換為比較兩個函式f(n)，g(n)的問題

要比較兩個函式的增長情況，最好的辦法是比較函式的一階導，這樣最精確，但是考慮到很多時候只需要大體瞭解演算法的優劣就可以了，所以我們就直接考察對增長速度影響最大的一項，這一項就是函式的最高階數。為了說明最高階數對函式增長影響最明顯，我們看兩幅圖。

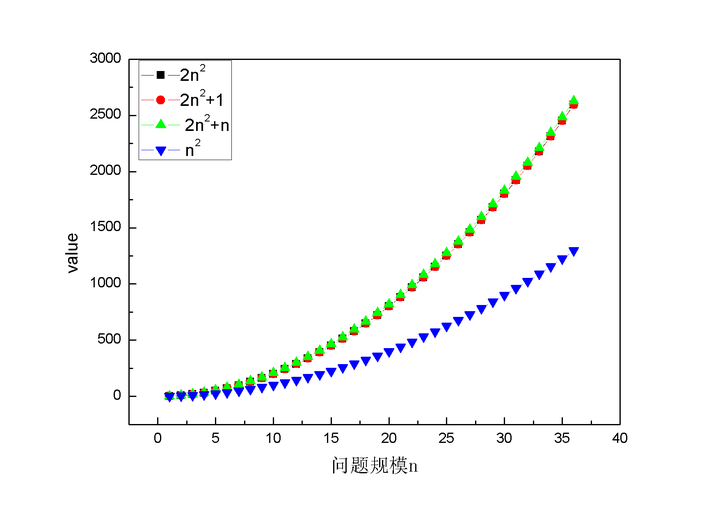
圖中4條曲線分別表示4種不同的執行次數表示式，從圖中可以看出，只要最高項的階數相同，4種表示式值受其他項的影響很小，隨著n增大，幾乎可以忽略不計，甚至可以忽略與最高項相乘的常數。

既然可以只考慮最高項的階數，以簡化問題，達到估算的目的，為何不這樣做呢？

那總得給這種情況一個恰當的表示方式吧？和其他領域一樣，還得用符號來表示，這個符號就是大名鼎鼎的大O。

T(n)=O(f(n))

其中，T(n)就是演算法的時間複雜度；

f(n)表示執行與演算法優劣和問題規模有關的執行數；

O()表示一種運算子號，和+-*/類似。作用就是去除其他項，包括與最高項相乘的常數，只保留最高項，比如f(n)=2n^2+1,O(f(n))=O(n^2)

好了，我們已經推匯出了時間複雜度的大O表示，應該對演算法時間複雜度有個不錯的認識了吧。

最後回顧一下推導過程：

演算法執行時間->4種因素影響->去除軟硬體因素，考慮演算法優劣和問題規模n兩種因素->演算法執行次數->簡化：忽略其他項->大O表示法表示演算法時間複雜度