作者：jliang

https://blog.csdn.net/jliang3

1.重點歸納

1）支援向量機（SVM）是一種二分類模型

（1）它的基本模型定義在特徵空間上的間隔最大化的線性分類器，間隔最大使它有別於感知機（感知機的損失函式只判斷是否正確分類）。

（2）SVM還包含核技巧，使它稱為實質上的非線性分類器。

（3）學習策略：間隔最大化，最終可轉化為一個凸二次規劃問題進行求解。

2）分類

• 硬間隔支援向量機：資料是線性可分
• 軟間隔支援向量機：資料近似線性可分
• 非線性支援向量機：資料線性不可分，使用核技巧及軟間隔最大化

3）核函式表示將輸入從輸入空間對映到特徵空間得到特徵向量之間的內積。通過使用核函式可以學習非線性支援向量機。

4）線性支援向量機原始問題目標函式

         目標函式：

         約束條件：

5）線性支援向量機使用拉格朗日對偶轉換的目標函式

         目標函式：

         約束條件：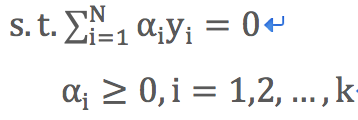

6）軟間隔線性支援向量機原始目標函式

         目標函式：

         約束條件：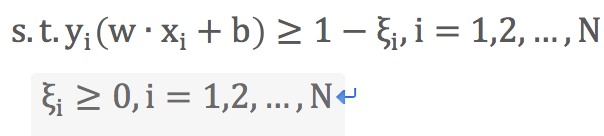

7）軟間隔線性支援向量機使用拉格朗日對偶轉換的目標函式

         目標函式：

         約束條件：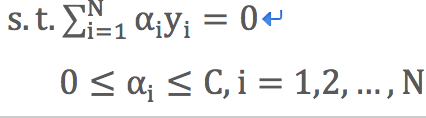

8）軟間隔線性支援向量機合頁損失函式

         取正值函式：

9）非線性支援向量機損失函式

         目標函式：

         約束條件：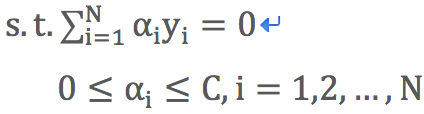

10）決策函式

       線性支援向量機時

2.線性可分支援向量機與硬間隔最大化

1）當訓練資料集線性可分時，存在無窮個分離超平面可將兩類資料正確分開。

（1）感知機利用誤分類最小的策略求得分離超平面，此時有無窮多個解。

（2）SVM利用間隔最大化求得最優分離超平面，這是的解是唯一的。

（3）分類超平面：w*∙x+b*=0

（4）分類決策函式：

         符號函式：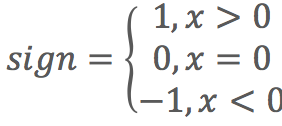

2）函式間隔：

（1）表示點x距離超平面的遠近，可以表示分類預測的確信程度；與類標y符號是否一致能夠表達分類是否正確。所以表示分類的正確性及確信度。

（2）當成倍地改變w和b值時（例如改為2w和2b），超平面沒有變化，但是函式間隔卻也成倍地改變了（上面例子變為2倍）。

3）幾何間隔：

（1）在函式間隔的基礎上，對分離超平面的法向量w加約束，規範化w=1使得間隔不變化。

（2）w為w的L2範數。

（3）函式間隔與幾何間隔的關係：

4）線性可分支援向量機目標函式：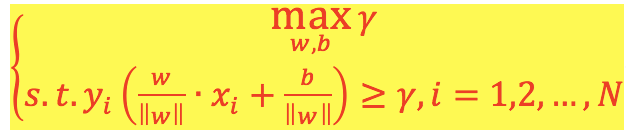

（1）最大化幾何間隔γ，約束條件為超平面(w,b)對每個訓練樣本點的幾何間隔至少為γ。

（2）使用代入函式得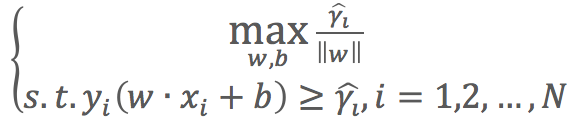：，的取值並不影響最優化問題的解。

（3）最大化和最小化是等價的，是凸函式，可以求最小值。

（4）簡化後的目標函式（原始目標函式）：

         目標函式：

         約束條件：

（5）求解目標函式可得分離超平面w*∙x+b*=0和分類決策函式w*∙x+b*=0

5）凸二次規劃問題

（1）凸優化問題：是指約束最優化問題

         目標函式：

         約束條件：

（2）目標函式f(w)和約束函式都是上的連續可微的凸函式，約束函式是上的仿射函式。

（3）當目標函式f(w)是二次函式且約束函式是仿射函式時，上述凸最優化問題成為凸二次規劃問題。

6）支援向量和間隔邊界

（1）訓練樣本中與分離超平面距離最近的樣本點稱為支援向量，支援向量使公式成立。

（2）由正負樣本支援向量組成的距離稱為間隔，間隔的兩個邊界稱為間隔邊界，即：

（3）只有支援向量了對決定分離超平面起作用，其他例項點不起作用。支援向量的個數一般很少，所以SVM由很少的“重要”訓練樣本確定。

7）對偶演算法

（1）通過拉格朗日對偶性變換到對偶變數的優化問題，即通過求解與原問題等價的對偶問題得到原始問題的最優解，這就是線性可分條件下支援向量機的對偶演算法。

（2）優點

• 對偶問題往往更容易求解
• 可以自然引入核函式，進而推廣到非線性分類問題

（3）拉格朗日對偶性求解過程

         目標函式：

         約束條件：