統計學習方法(李航)筆記
感知機/k近鄰/貝葉斯/決策樹
前言:有時候公式實在不好理解的時候可以看一道例題理解,或者執行程式debug除錯逐步看輸入輸出變化進行理解!
第二章感知機
感知機概念
輸入到輸出空間的對映:f(x) =sign(w*x+b)
sign函式如下:
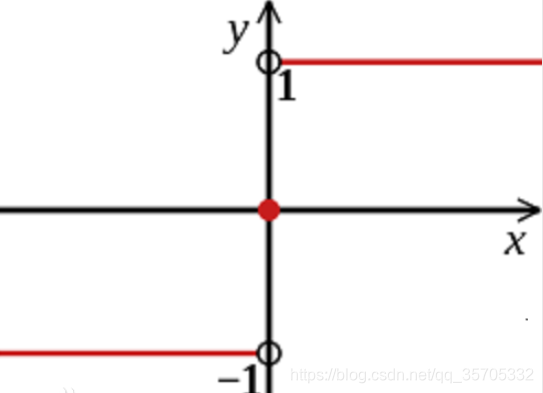
感知器是一種線性分類器模型,屬於判別模型。
感知機是採用隨機梯度下降,是在所有誤分點中隨機選一個誤差點的梯度下降來跟新其的權重和偏執。
感知機學習演算法原始形式
跟新權重與bias的方法也是梯度下降法:

具體演算法實現步驟如下:

感知機的對偶形式
推導過程:
原始公式中權重與偏執的變化如下:
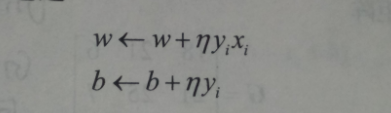
當w,b初始值設定為0時,上式可以變換為下面的式子,
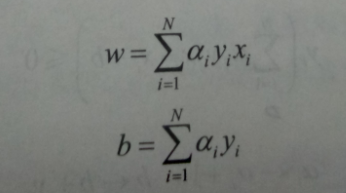
相當於w,b的迭代跟新轉換到a上,具體如下,而對於a來說,每次迭代增量都是學習率,計算到最後一次後就是累加選中相應樣本的次數*學習率。

感知機模型對偶形式:出現了內積的形式
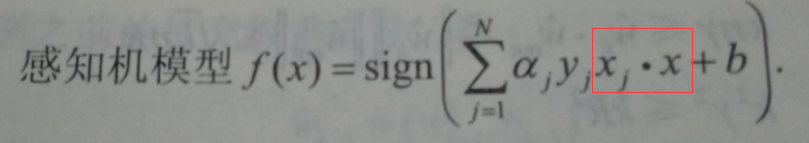
第三章 k近鄰
概念
K近鄰:利用歐氏距離衡量,計算要預測的點與已知點的距離,選取距離最近的K個樣本點作為參考,接著使用多數表決法從k個最近的樣本點判斷預測點屬於哪個類。多數表決法即K個點中屬於C的類別數目多,支援為C類的多,則判定為C類。
k近鄰演算法的實現——KDTree的構造
實質就是中位數排序,以中位數劃分子樹。如圖所示,首先利用第一維的資料進行中位數選擇,緊接著利用第二維的資料特徵做中位數排序…

k近鄰演算法的實現——KDTree的搜尋
緊接著搜尋樹,有一種2分法的感覺,比線性掃描節省了太多時間!!線性掃描就是輸入一個數對訓練例項的每一個計算距離。。。。。
輸入待檢測點為(2,2,2)
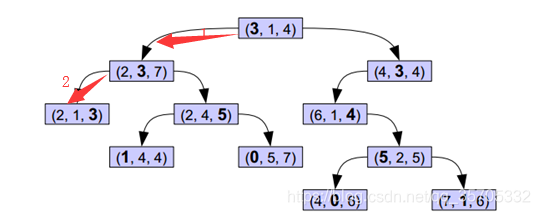
分別計算葉子結點(2,1,3),(2,3,7),(3,1,4)與待檢測點歐氏距離,回溯到根節點距離最小為最近點。。。。。當訓練資料較多依然計算量很大。
第4章 樸素貝葉斯
基本概念
先驗概率:用P(Bi)表示沒有訓練資料前假設h擁有的初始概率,稱為先驗概率。
後驗概率: P(Bi|A)為後驗概率,給定A時Bi成立的概率,稱為Bi的後驗概率;
貝葉斯公式:
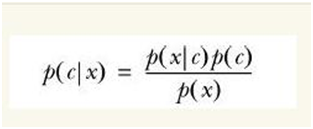
分類問題
假設之前已經統計了兩類的分佈情況,我們可以用p1(x,y)表示資料點(x,y)屬於紅色一類的概率,同時也可以用p2(x,y)表示資料點(x,y)屬於藍色一類的概率。出現一個新的點new_point (x,y),其分類未知。那要把new_point歸在紅、藍哪一類呢?
一般用貝葉斯公式的分子替代整體:
如果p(red|x,y) > p(blue|x,y), 則(x,y)屬於紅色一類。
如果p(red|x,y) < p(blue|x,y), 則(x,y)屬於藍色一類。
最大似然估計——求模型引數
給定一堆資料,假如我們知道它是從某一種分佈中隨機取出來的,可是我們並不知道這個分佈具體的參,即“模型已定,引數未知”。例如,我們知道這個分佈是正態分佈,但是不知道均值和方差;或者是二項分佈,但是不知道均值。 最大似然估計(MLE,Maximum Likelihood Estimation)就可以用來估計模型的引數。但是在實際問題中並不都是這樣幸運的,我們能獲得的資料可能只有有限數目的樣本資料,而先驗概率 和類條件概率(各類的總體分佈) 都是未知的。
貝葉斯演算法實現流程


第五章 決策樹
概念
決策樹由結點和有向邊組成。內部結點表示一個特徵或者屬性,葉子結點表示類別。樹結構如圖:
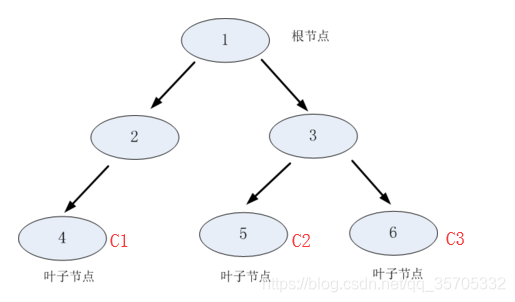
主要包含三部分:特徵選擇/決策樹的生成/決策樹剪枝;決策樹學習就是尋找最優特徵~
特徵選擇——資訊增益、資訊增益比
1.資訊增益
熵:表示隨機變數不確定性的度量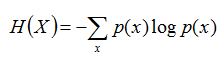
聯合熵:兩個隨機變數X,Y的聯合分佈,可以形成聯合熵Joint Entropy,用H(X,Y)表示。
條件熵:在隨機變數X發生的前提下,隨機變數Y發生所新帶來的熵定義為Y的條件熵,用H(Y|X)表示,用來衡量在已知隨機變數X的條件下隨機變數Y的不確定性。
== 資訊增益演算法==
輸入:訓練資料集D和特徵A;輸出特徵A對訓練集D的資訊增益g(D,A).

2.== 資訊增益比==
主要解決資訊增益的問題,資訊增益容易造成選擇取值較多的特徵~~

決策樹生成
-
ID3演算法
應用資訊增益準則選擇特徵,遞迴地構建決策樹

-
C4.5演算法
用資訊增益比來選擇特徵,構建決策樹

決策樹的剪枝
為了防止過擬合,需要對決策樹進行裁剪。裁剪分為事前裁剪和事後裁剪。事前裁剪髮生在建立決策樹時,通過判定規則(例如節點總數>),來決定是否進行新的分級。 事後裁剪髮生在建立決策樹後,通過判定規則進行樹的修剪。準則:極小化決策樹整體的損失函式。
理想的決策樹有三種:
1.葉子節點數最少
2.葉子加點深度最小
3.葉子節點數最少且葉子節點深度最小。
預剪枝,設定樹的深度為3,深度大於3的部分都不會構建;或者設定當分支樣本數量小於50就停止構建樹等等要求,在構建樹的時候就進行剪枝;
後剪枝,由下圖損失函式公式所示,葉子結點個數作為一個正則化項,希望葉子結點也少越好;前面一項為經驗熵。

經驗熵公式:
分別計算剪前葉子結點的損失函式與剪後葉子結點損失函式,對比,剪前大就直接減掉~
Ntk:對應葉結點中k類的樣本點個數;
Nt:對應葉結點樣本的個數
T:|T|為葉子結點個數
t:是樹T的葉子結點
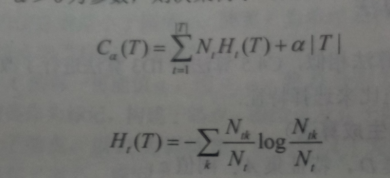
每一個葉子結點樣本數乘上葉子結點的熵


剪枝過程的理解: