[圖形學] 布料模擬(質點彈簧模型)
寫給我的室友:
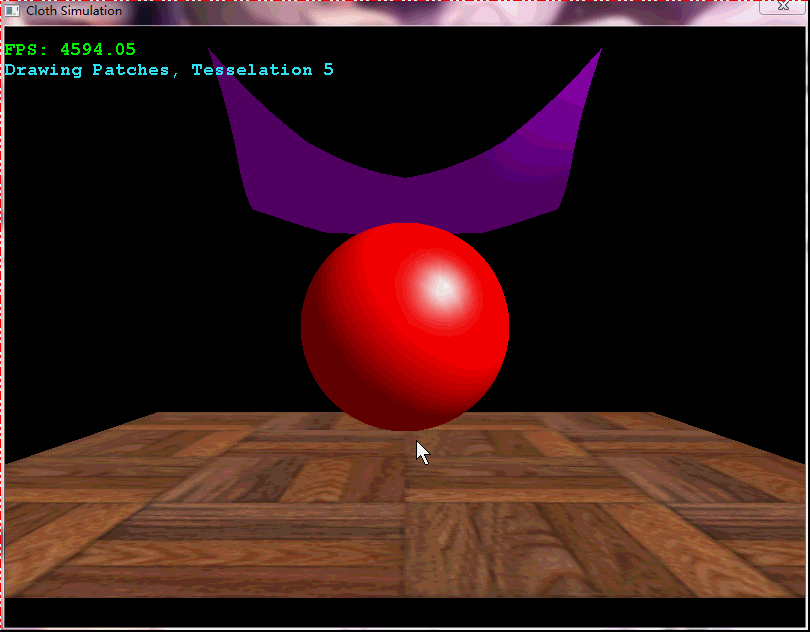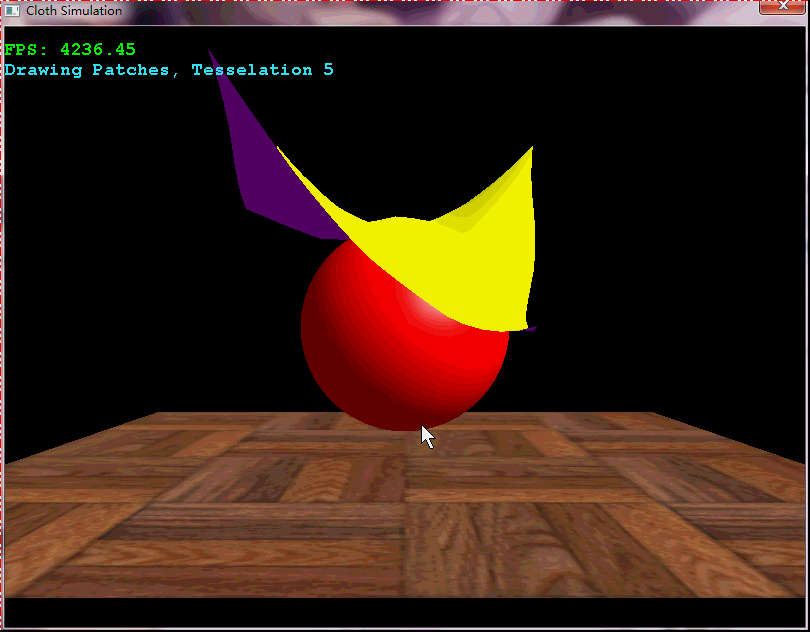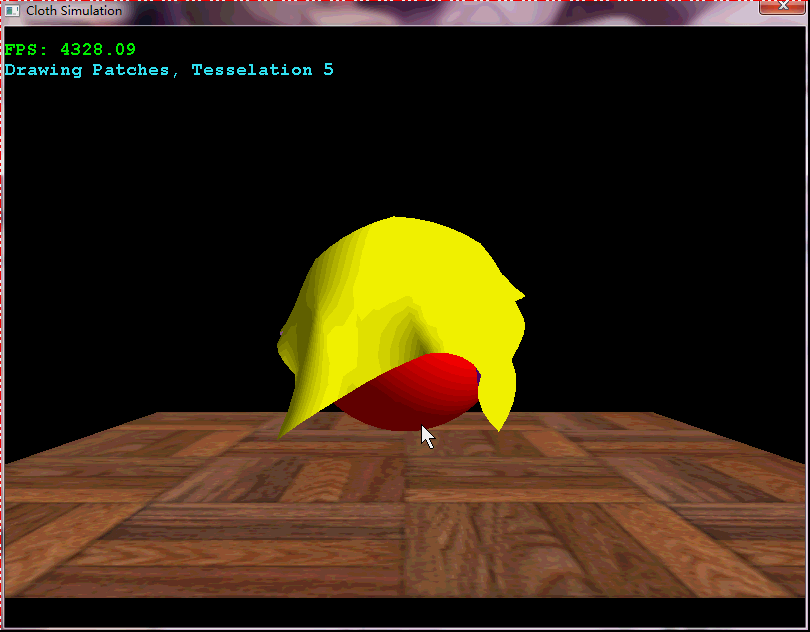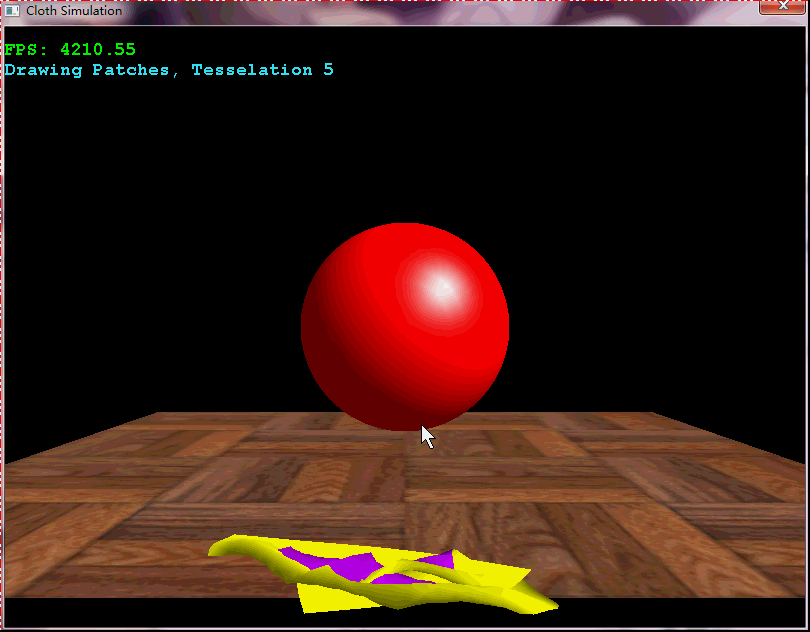
布料模擬的常用方法就是將布料表達為三維網格,然後通過彈力+外力進行布料模擬。它在遊戲中有著廣泛的應用,如衣袖的擺動,旗幟的飄動;此外,也可以用於模擬試衣等。
模型初始化
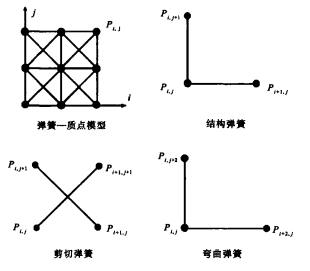
在質點彈簧模型中,整個布料由網格點表達,而點與點之間的連線,我們稱之為彈簧。
布料一個點的位置是由它周圍的12個點控制的。其中8個是相鄰點,另外4個是隔點的鄰接點。
對於彈簧而言,存在三種彈簧,一種是結構彈簧,一種是剪下彈簧,還有一種是彎曲彈簧。它們分別與上圖12根彈簧對應。
其中,結構彈簧模擬的是橫向的力,為了阻止布料在橫向產生較大的拉壓變形。
剪下彈簧同理,是為了阻止布料在斜向產生較大的拉壓變形。
而彎曲彈簧連線了兩個相隔的點,它主要作用是在布料發生彎曲形變的時候,阻止它的過度彎曲,導致布料的角一下子坍塌。這個係數有時候也可以不考慮。
在具體的程式碼實現中,我們初始化點的位置、速度(初始化為0),質量(設為統一的值),以及是否固定(固定後將不受外力,即重力)。
接下來,執行六個迴圈,來初始化彈簧,對應於上圖,可以避免重複邊計算。對於彈簧,我們需要指定兩個端點,彈性係數(所有的彈簧都一樣),初始長度(跟位置有關,上下左右為1,斜邊為根號2,紅色邊為2)
//The first (gridSize-1)*gridSize springs go from one ball to the next, //excluding those on the right hand edge for(int i=0; i<gridSize; ++i) { for(int j=0; j<gridSize-1; ++j) { currentSpring->ball1=i*gridSize+j; currentSpring->ball2=i*gridSize+j+1; currentSpring->springConstant=springConstant; currentSpring->naturalLength=naturalLength; ++currentSpring; } } //The next (gridSize-1)*gridSize springs go from one ball to the one below, //excluding those on the bottom edge for(int i=0; i<gridSize-1; ++i) { for(int j=0; j<gridSize; ++j) { currentSpring->ball1=i*gridSize+j; currentSpring->ball2=(i+1)*gridSize+j; currentSpring->springConstant=springConstant; currentSpring->naturalLength=naturalLength; ++currentSpring; } } //The next (gridSize-1)*(gridSize-1) go from a ball to the one below and right //excluding those on the bottom or right for(int i=0; i<gridSize-1; ++i) { for(int j=0; j<gridSize-1; ++j) { currentSpring->ball1=i*gridSize+j; currentSpring->ball2=(i+1)*gridSize+j+1; currentSpring->springConstant=springConstant; currentSpring->naturalLength=naturalLength*sqrt(2.0f); ++currentSpring; } } //The next (gridSize-1)*(gridSize-1) go from a ball to the one below and left //excluding those on the bottom or right for(int i=0; i<gridSize-1; ++i) { for(int j=1; j<gridSize; ++j) { currentSpring->ball1=i*gridSize+j; currentSpring->ball2=(i+1)*gridSize+j-1; currentSpring->springConstant=springConstant; currentSpring->naturalLength=naturalLength*sqrt(2.0f); ++currentSpring; } } //The first (gridSize-2)*gridSize springs go from one ball to the next but one, //excluding those on or next to the right hand edge for(int i=0; i<gridSize; ++i) { for(int j=0; j<gridSize-2; ++j) { currentSpring->ball1=i*gridSize+j; currentSpring->ball2=i*gridSize+j+2; currentSpring->springConstant=springConstant; currentSpring->naturalLength=naturalLength*2; ++currentSpring; } } //The next (gridSize-2)*gridSize springs go from one ball to the next but one below, //excluding those on or next to the bottom edge for(int i=0; i<gridSize-2; ++i) { for(int j=0; j<gridSize; ++j) { currentSpring->ball1=i*gridSize+j; currentSpring->ball2=(i+2)*gridSize+j; currentSpring->springConstant=springConstant; currentSpring->naturalLength=naturalLength*2; ++currentSpring; } }
加入外力並更新位置
對於布料,維護兩個狀態,當前狀態和下一狀態,每隔10ms,我們根據已知的當前資訊,根據公式計算下一狀態資訊,然後把下一狀態轉移為當前狀態。首先,我們計算每根彈簧形變產生的壓力。
//Calculate the tensions in the springs //計算彈簧壓力 for(int i=0; i<numSprings; ++i) {//彈簧長度 = 前一個彈簧的位置 - 下一個彈簧的位置 float springLength=( currentBalls[springs[i].ball1].position- currentBalls[springs[i].ball2].position).GetLength(); //伸展 = 現在長度 - 原始長度 float extension=springLength-springs[i].naturalLength; //壓力 = 彈性係數 * 伸展 / 自然長度 springs[i].tension=springs[i].springConstant*extension/springs[i].naturalLength; }
在這裡使用的公式為 F = k△x。在上面程式碼中,又除以了自然長度,這是因為對於物理上完全相同的彈簧而言,彈性係數與長度有關,而在這裡我們設為相同的,為了抵消這種影響,需要消除這個引數。
我們需要注意k的選取:如果k太小,布料就會過於柔軟,呈現凹陷的狀態,而如果k太大,布料會顯得過於僵硬。
如果該點不是固定的,那麼需要計算外力。
對於每個彈簧,我們對它的兩個端點加上這個彈簧的彈力以及外力(在這裡,外力為重力)。
//Loop through springs
for (int j = 0; j<numSprings; ++j)
{
//If this ball is "ball1" for this spring, add the tension to the force
if (springs[j].ball1 == i)
{
VECTOR3D tensionDirection = currentBalls[springs[j].ball2].position -
currentBalls[i].position;
tensionDirection.Normalize();
//把力加上去
force += springs[j].tension*tensionDirection;
}
//Similarly if the ball is "ball2"
if (springs[j].ball2 == i)
{
VECTOR3D tensionDirection = currentBalls[springs[j].ball1].position -
currentBalls[i].position;
tensionDirection.Normalize();
force += springs[j].tension*tensionDirection;
}
}得到外力後,我們根據牛頓第二定律計算每個控制點新的位置:
//計算加速度
//Calculate the acceleration
VECTOR3D acceleration = force / currentBalls[i].mass;
//更新速度
//Update velocity
nextBalls[i].velocity = currentBalls[i].velocity + acceleration*
(float)timePassedInSeconds;
//減少速度
//Damp the velocity
nextBalls[i].velocity *= dampFactor;
//Calculate new position
//計算新的位置
nextBalls[i].position = currentBalls[i].position +
(nextBalls[i].velocity + currentBalls[i].velocity)*(float)timePassedInSeconds / 2;
之後,對球體和地板進行碰撞檢測:
//Check against sphere (at origin)
//計算球體
if (nextBalls[i].position.GetSquaredLength()<sphereRadius*1.08f*sphereRadius*1.08f)
nextBalls[i].position = nextBalls[i].position.GetNormalized()*
sphereRadius*1.08f;
//Check against floor
if (nextBalls[i].position.y<-8.5f)
nextBalls[i].position.y = -8.5f;最終把下一狀態轉移到當前狀態,並計算新的法線(根據兩個向量的叉積):
//Calculate the normals on the current balls
for (int i = 0; i<gridSize - 1; ++i)
{
for (int j = 0; j<gridSize - 1; ++j)
{
VECTOR3D & p0 = currentBalls[i*gridSize + j].position;
VECTOR3D & p1 = currentBalls[i*gridSize + j + 1].position;
VECTOR3D & p2 = currentBalls[(i + 1)*gridSize + j].position;
VECTOR3D & p3 = currentBalls[(i + 1)*gridSize + j + 1].position;
VECTOR3D & n0 = currentBalls[i*gridSize + j].normal;
VECTOR3D & n1 = currentBalls[i*gridSize + j + 1].normal;
VECTOR3D & n2 = currentBalls[(i + 1)*gridSize + j].normal;
VECTOR3D & n3 = currentBalls[(i + 1)*gridSize + j + 1].normal;
//Calculate the normals for the 2 triangles and add on
VECTOR3D normal = (p1 - p0).CrossProduct(p2 - p0);
n0 += normal;
n1 += normal;
n2 += normal;
normal = (p1 - p2).CrossProduct(p3 - p2);
n1 += normal;
n2 += normal;
n3 += normal;
}
}
//Normalize normals
for (int i = 0; i<numBalls; ++i)
currentBalls[i].normal.Normalize();
}拓展
以上演算法提供了布料模擬的一個基本雛形,在可擴充套件性上,可以考慮到這些問題:
1) 沒有精確的碰撞檢測(包括自身的碰撞建策 和 與外物的碰撞檢測)
2) 布料是純光滑的,沒有考慮到質地(摩擦因子)
3) 外力較為單一
4)把布料抽象為面片,沒有考慮到厚度