題目連結：這裡

或者這裡

答案是很顯然的，記\(g(i)\)為在\(i\)下平衡木時的期望收益

那麼\(g(i)=max(f(i),\frac{g(i-1)+g(i+1)}{2})\)

好了做完了

TMD這個式子有和沒有有什麼區別啊（還是有區別的）

我們考察那些\(g(i)=f(i)\)的點

更特殊的，我們考慮點\((i,f(i))\)在二維座標上的分佈，同時由\(f(0)=f(n+1)=0\)我們再加入兩個新點\((0,0)\)和\((n+1,0)\)

那麼樣例的圖就是這樣子的

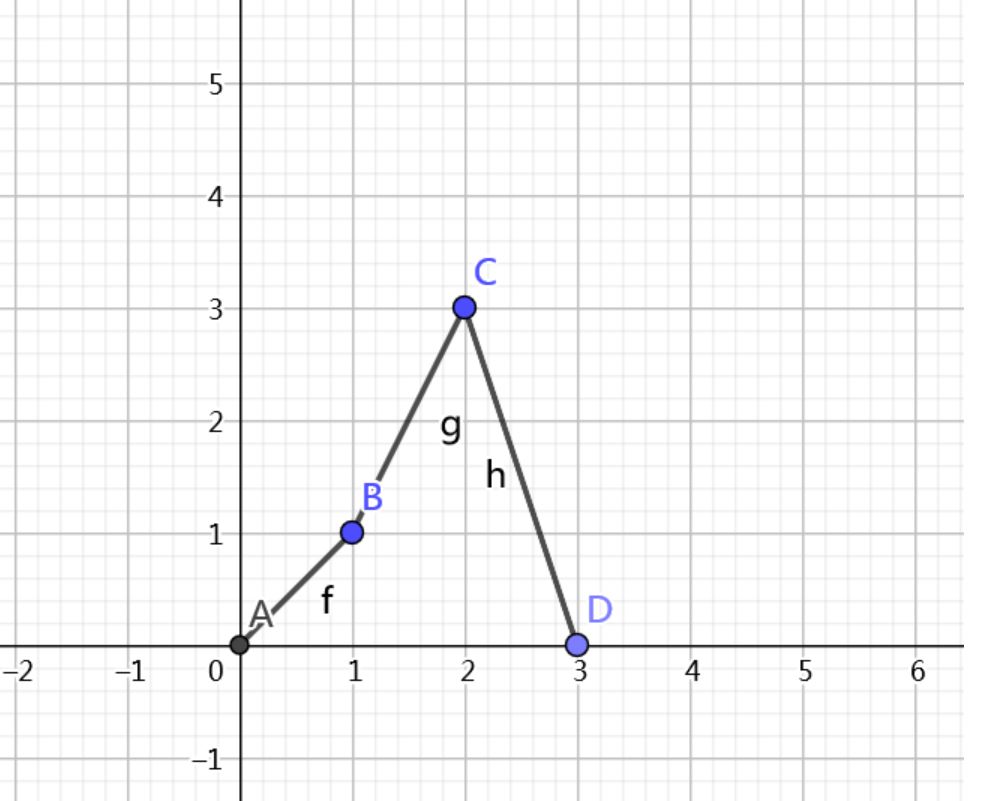
我們再來看一下期望在這個平面上的分佈（圖中的紅線）

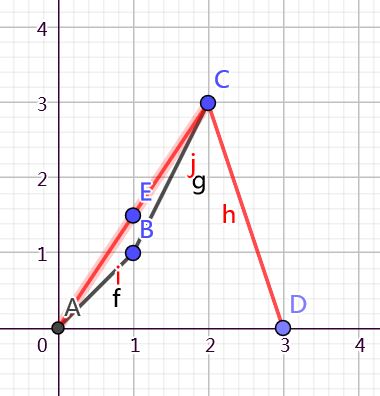
我們會發現，在1處的期望是AC兩點的連線在\(x=1\)

這是不是偶然？

我們重新回到一開始的式子\(g(i)=max(f(i),\frac{g(i-1)+g(i+1)}{2})\)

\(g(i)\)就是一開始出現在圖一中的點，而\(\frac{g(i-1)+g(i+1)}{2}\)則是這個點兩端的點的連線在\(i\)上的取值

而我們的\(g(i)\)是在這兩者之間取一個max

也就是說所有的\(g(i)\)應該在所有的\(f(i)\)的點所構成的一個上凸包上

這樣我們就可以先把凸包跑出來，再記錄下這個點兩端的凸包的點，在凸包上的點\(f(i)\)就是其期望

其它點運用一次函式的相關知識解出期望即可

#include<iostream>
#include<string>
#include<string.h>
#include<stdio.h>
#include<algorithm>
#include<math.h>
#include<vector>
#include<queue>
#include<map>
using namespace std;
#define rep(i,a,b) for (i=a;i<=b;i++)
typedef long long ll;
#define maxd 1e5
ll f[100100],l[100100],r[100100],hull[100100];
int n,top=0;

int read()
{
    int x=0,f=1;char ch=getchar();
    while ((ch<'0') || (ch>'9')) {if (ch=='-') f=-1;ch=getchar();}
    while ((ch>='0') && (ch<='9')) {x=x*10+(ch-'0');ch=getchar();}
    return x*f;
}

int main()
{
    n=read();int i,j;
    for (i=1;i<=n;i++) f[i]=read();
    hull[++top]=0;
    for (i=1;i<=n+1;i++)
    {
        while (top>=2)
        {
            int a=hull[top],b=hull[top-1];
            //cout << top << endl;
            if ((f[a]-f[b])*(i-a)<(f[i]-f[a])*(a-b)) top--;
            else break;
        }
        hull[++top]=i;
    }
    //for (i=1;i<=top;i++) cout << hull[i] << " ";cout << endl;

    for (i=1;i<top;i++)
    {
        for (j=hull[i]+1;j<hull[i+1];j++)
        {
            l[j]=hull[i];r[j]=hull[i+1];
        }
        l[hull[i]]=hull[i];r[hull[i]]=hull[i];
    }
    l[n+1]=n+1;r[n+1]=n+1;
    //for (i=0;i<=n+1;i++) cout << l[i] << " ";cout << endl;
    //for (i=0;i<=n+1;i++) cout << r[i] << " ";cout << endl;
    for (i=1;i<=n;i++)
    {
        ll ans=0;
        if (l[i]==r[i]) ans=f[i]*maxd;
        else ans=(maxd*(f[l[i]]*(r[i]-i)+f[r[i]]*(i-l[i])))/(r[i]-l[i]);
        printf("%lld\n",ans);
    }
    return 0;
}