JavaScript實現樹結構(二)
阿新 • • 發佈:2020-03-11
## JavaScript實現樹結構(二)
### 一、二叉搜尋樹的封裝
**二叉樹搜尋樹的基本屬性**:
如圖所示:二叉搜尋樹有四個最基本的屬性:指向節點的**根**(root),節點中的**鍵**(key)、**左指標**(right)、**右指標**(right)。
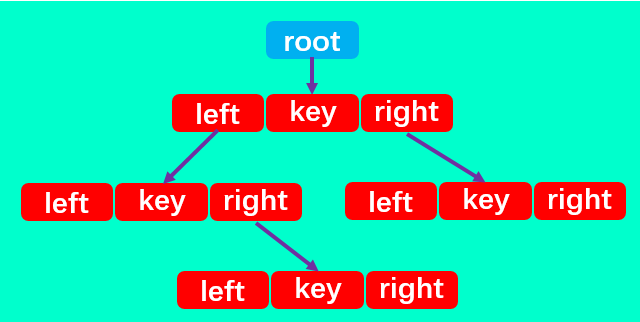
所以,二叉搜尋樹中除了定義root屬性外,還應定義一個節點內部類,裡面包含每個節點中的left、right和key三個屬性:
```javascript
//封裝二叉搜尋樹
function BinarySearchTree(){
//節點內部類
function Node(key){
this.key = key
this.left = null
this.right = null
}
//屬性
this.root = null
}
```
**二叉搜尋樹的常見操作:**
* insert(key):向樹中插入一個新的鍵;
* search(key):在樹中查詢一個鍵,如果節點存在,則返回true;如果不存在,則返回false;
* inOrderTraverse:通過中序遍歷方式遍歷所有節點;
* preOrderTraverse:通過先序遍歷方式遍歷所有節點;
* postOrderTraverse:通過後序遍歷方式遍歷所有節點;
* min:返回樹中最小的值/鍵;
* max:返回樹中最大的值/鍵;
* remove(key):從樹中移除某個鍵;
#### 1.插入資料
**實現思路:**
* 首先根據傳入的key建立節點物件;
* 然後判斷根節點是否存在,不存在時通過:this.root = newNode,直接把新節點作為二叉搜尋樹的根節點。
* 若存在根節點則重新定義一個內部方法insertNode()用於查詢插入點。
```JavaScript
//insert方法:對外向使用者暴露的方法
BinarySearchTree.prototype.insert = function(key){
//1.根據key建立節點
let newNode = new Node(key)
//2.判斷根節點是否存在
if (this.root == null) {
this.root = newNode
//根節點存在時
}else {
this.insertNode(this.root, newNode)
}
}
```
**內部方法insertNode()的實現思路**:
根據比較傳入的兩個節點,一直查詢新節點適合插入的位置,直到成功插入新節點為止。
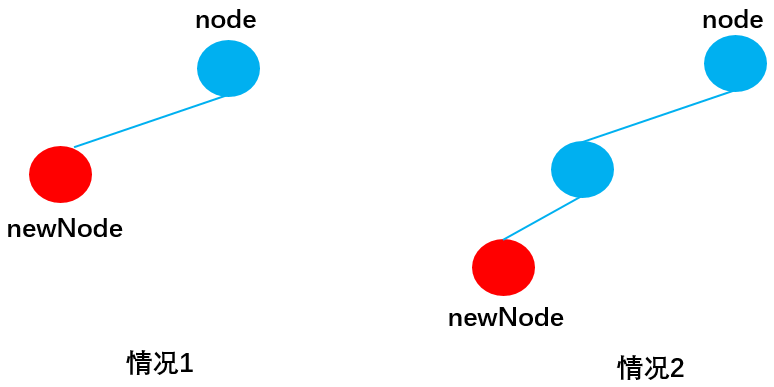
當newNode.key < node.key向左查詢:
* 情況1:當node無左子節點時,直接插入:
* 情況2:當node有左子節點時,遞迴呼叫insertNode(),直到遇到無左子節點成功插入newNode後,不再符合該情況,也就不再呼叫insertNode(),遞迴停止。
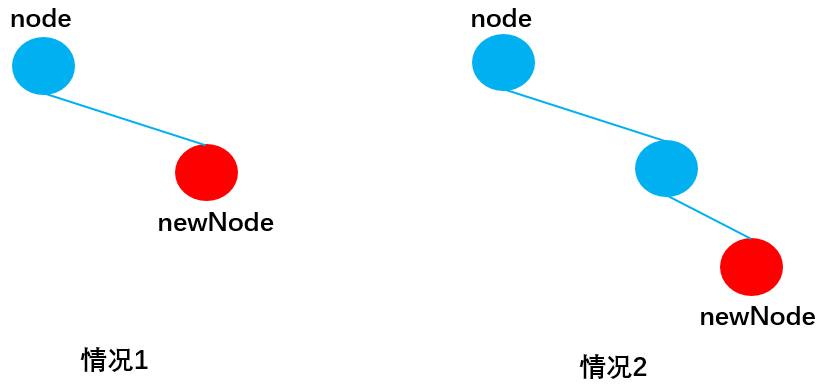
當newNode.key >= node.key向右查詢,與向左查詢類似:
* 情況1:當node無右子節點時,直接插入:
* 情況2:當node有右子節點時,依然遞迴呼叫insertNode(),直到遇到傳入insertNode方法的node無右子節點成功插入newNode為止:
**insertNode()程式碼實現:**
```
//內部使用的insertNode方法:用於比較節點從左邊插入還是右邊插入
BinarySearchTree.prototype.insertNode = function(node, newNode){
//當newNode.key < node.key向左查詢
/*----------------------分支1:向左查詢--------------------------*/
if(newNode.key < node.key){
//情況1:node無左子節點,直接插入
/*----------------------分支1.1--------------------------*/
if (node.left == null) {
node.left = newNode
//情況2:node有左子節點,遞迴呼叫insertNode(),直到遇到無左子節點成功插入newNode後,不再符合該情況,也就不再呼叫insertNode(),遞迴停止。
/*----------------------分支1.2--------------------------*/
}else{
this.insertNode(node.left, newNode)
}
//當newNode.key >
